Связь между напряжениями и деформациями. Закон Гука.

Как уже упоминалось ранее, между напряжениями и деформациями существует связь, которая может быть установлена лишь экспериментальным путем.

Большинство твердых тел, при сравнительно небольших нагрузках, обнаруживают свойство однозначной зависимости между напряжениями и деформациями (или между силами и перемещениями).

Например, если вспомнить известные нам из курса лабораторных работ диаграммы растяжения и сжатия малоуглеродистой стали, то можно заметить, что вплоть до значений напряжения равного - предела пропорциональности зависимость между напряжениями и деформациями близка к линейной.

Подобная картина наблюдается и у других сталей, а также, может быть менее отчетливо, у других материалов. Данный экспериментальный факт позволяет принять простейший из упругих законов – закон Гука, т.е. закон линейной упругости:

Напряжения пропорциональны деформациям

Коэффициент пропорциональности между напряжениями и деформациями называется модулем упругости первого рода (модулем Юнга). Модуль упругости определяется опытным путем и служит мерой жесткости материала. Геометрический смысл - угловой коэффициент прямолинейного начального участка диаграммы материала.

Модуль упругости для некоторых, часто применяемых материалов, имеет приблизительно следующие значения.

Сталь: ; Медь: ;

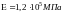Дерево: 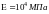; Каучук:

Отметим еще раз, что свойство упругости, в частности линей-

ной упругости, относительно. Уместно говорить не о упругих и неупругих материалах, а о упругом и неупругом состоянии материала.

Если в (3) выразить по формуле (2) и учесть (1), то получим закон Гука в форме, позволяющей находить удлинения.

Величину называют жесткостью при растяжении-сжатии. Закон (4) можно сформулировать следующим образом: удлинение стержня прямо пропорционально нормальной силе и длине стержня и обратно пропорционально жесткости при растяжении-сжатии.

По формуле (4) можно определять удлинения только в том

случае, если нормальная сила и поперечное сечение постоянны по

длине стержня, т.е. если напряженное состояние однородно.

Если нормальная сила и поперечное сечение меняются по длине ступенчато, то стержень надо разбить на участки, так чтобы в пределах каждого участка и были постоянны, определить удлинение каждого из участков и тогда полное удлинение стержня будет равняться алгебраической сумме, (знак определяется знаком ) удлинений участков.

Если же напряженное состояние в стержне неоднородно, то выделив малый элемент длиной определим его удлинение

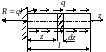
, Здесь и рассматривается как функции z. Полное удлинение стержня будет равно:

Теорема о работе статической силы, приложенной к упругой системе (Теорема Клапейрона).

Работа статической силы, приложенной к упругой системе, равняется половине произведения окончательного значения силы на окончательное значение перемещения.

Пусть - сила, изменяющаяся на сегменте а

- перемещение, изменяющееся в пределах . Система линейно упруга и сила связана с перемещением законом Гука , где 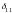- перемещение, вызванное силой Тогда

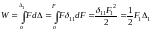
Эта теорема, носящая имя Клапейрона, имеет простую геометрическую интерпретацию.

Л егко понять, что множитель у работы, равный появляется по той причине, что сила не постоянна, а меняется по линейному закону.