Растяжение и сжатие
Растяжением будем называть такое нагружение стержня, когда в поперечных сечениях возникает лишь один внутренний силовой фактор – нормальная сила.
Для того чтобы возникло растяжение необходимо, чтобы внешние силы, приложенные по торцам стержня, были статически эквивалентны сосредоточенной силе, приложенной по оси стержня.
Схематизируя силы, приложенные к стержню, мы используем принцип Сен-Венана, который в данном конкретном случае примет следующий вид: “Способ приложения нагрузки не сказывается в сечениях достаточно удаленных от места приложения нагрузки”.
Н
апример,
стержень одной и той же длины и сечения
загружается разным образом. В первом
случае имеется закладная головка,
которая помещена в захваты испытательной
машины, во втором случае она представляет
собой равнодействующую давления со
стороны болта или заклепки. Безусловно,
что характер распределения напряжений
в месте передачи нагрузки, совершенно
различный и весьма сложный. Однако, на
расстояниях равных примерно характерному
размеру поперечного сечения,
индивидуальности в передачи нагрузки
не сказываются, и для обоих случаев
может быть принята одна и та же расчетная
схема: Стержень загружен по торцам
сосредоточенными силами, направленными
по оси.
Параллельно с растяжением мы будем рассматривать и случай сжатия, отличая его от растяжения лишь знаком нормальной силы и напряжения. Но в данной лекции мы будем рассматривать сжатие коротких стержней, длина которых не превышает нескольких размеров поперечного сечения.
Однородное растяжение.
П
редставим
себе случай, что по торцам стержня
приложены равномерно распределенные
силы. Тогда в любом поперечном сечении
напряжения будут направлены по нормали
и будут постоянны во всех точках.
Напряженное состояние будет однородным,
т.е. одинаковым во всех точках стержня.
Напряжения при растяжении и сжатии.
Рассмотрим стержень, растянутый по торцам силами.
О
пределим
в некотором произвольном сечении
нормальную силу и напряжения. Воспользуемся
методом сечений, рассечем стержень на
две части и рассмотрим равновесие одной
из них. Очевидно, что нормальная сила
.
Далее, используя принцип Сен-Венана, приходим к выводу,
ч
то
напряженное состояние должно быть точно
таким же, как и в случае однородного
растяжения, рассмотренном выше. Таким
образом, если
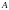- площадь поперечного сечения стержня,
то при равномерном характере распределения
напряжений.
- нормальная сила равна
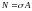
При
растяжении (сжатии) нормальные напряжения
распределены по сечению равномерно и
равняются нормальной силе, деленной на
площадь поперечного сечения.
(1)
Нормальным силам и напряжениям предписывается знак: при растяжении плюс, при сжатии минус.
Деформированное состояние при растяжении и сжатии.
Т.к. напряженное состояние однородно, то однородным будет и деформированное состояние. Любой элемент объема будет деформироваться одинаково. Поперечные сечения стержня останутся плоскими, и будут удаляться друг от друга при растяжении и сближаться при сжатии. Этот факт можно положить в основу всей теории и сформулировать как гипотезу плоских сечений: сечения плоские и нормальные к оси до деформации остаются плоскими и нормальными к оси после деформации.
Определим удлинения и деформации, возникающие в стержне.
П
усть
- длина стержня до деформации,
- длина стержня после деформации. Величину
называют продольным удлинением. Т.к.
деформированное состояние однородно,
то деформация не зависит от базы
измерения. Деформация в направлении
оси стержня равняется:
(2) Эта величина называется
относительным удлинением стержня.
Продольная
деформация ( в направлении оси стержня)
сопровождается поперечной:
,
где
-
характерный размер поперечного сечения
до деформации;
-
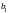то же самое после деформации.
Знаки продольной и поперечной деформаций противоположны. Продольное удлинение сопровождается уменьшением поперечных
размеров и наоборот.
Отношение
деформации поперечной к деформации
продольной есть для данного материала
величина постоянная, называется
коэффициентом Пуассона.
Для сталей эта величина колеблется в пределах 0,25 – 0,35.