Напряжение.

Мерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.

Р ассмотрим тело, находящееся под действием системы уравновешенных сил.

Будем исследовать внутренние силы в малой области, окружающей точку А. Проведем через данную точку сечение некоторой поверхностью. Внешняя нормаль этой поверхности в точке А - Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку . Результирующая внутренних сил, действующих на площадке пусть равняется .

Д елим результирующую силу на 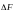, получаем величину среднего напряжения по площадке . Величина 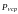зависит от размеров площадки, перейдем к пределу, стягивая площадку к точке

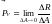
Величина - называется вектором полного напряжения в данной точке по площадке с внешней нормалью .

О чевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.

Совокупность всех векторов полного напряжения по площадкам, проходящим через данную точку, составляет напряженное состояние в данной точке.

Величину обычно раскладывают на две составляющие: нормальное напряжение , направленное по внешней нормали к площадке и касательное напряжение , лежащее в плоскости площадки.

Перемещения и деформации.

Рассмотрим тело, имеющее такое количество связей, что движение его как жесткого тела исключено. Перемещения точек тела обусловлены деформативностью материала.

П усть под действием сил тело деформировалось, и точка 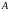перешла в новое положение . Тогда вектор 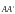называется вектором перемещения, а его проекции на координатные оси обозначены соответственно

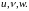
Зададим в точке 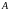некоторое направление и пусть длина отрезка В деформированном состоянии длина отрезка изменилась и стала равной Тогда величину

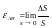называют линейной деформацией в данной точке по направлению АВ. Пусть угол между отрезками ЕС и ЕD – прямой.

После деформации тела величина угла изменится.

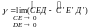Величина называется угловой деформацией или углом сдвига.

Уже сейчас отметим, что между напряжениями и деформациями существует связь, и эта связь принципиально может быть установлена только экспериментальным путем.

Принципы сопротивления материалов.

Таких принципов (основных правил) три.

1. Принцип неизменности начальных размеров.

Б удем считать, что перемещения, возникающие в системах, малы по сравнению с их размерами.

Так, например, определяя изгибающий момент в балке, мы не учитываем того обстоятельства, что в результате изгиба балки плечо у силы изменится.

2. Принцип независимости действия сил.

Если на систему действуют несколько сил, то напряжения (перемещения, деформации, внутренние силовые факторы), возникающие от совместного действия этих сил, можно определить следующим образом: определить от действия каждой из сил порознь и результаты сложить.

Справедливость этого принципа вытекает из принятия изложенного выше принципа неизменности начальных размеров и допущения, что между напряжениями и деформациями существует связь, определяемая простейшим законом – законом линейной упругости (закон Гука). В этом случае поведение наших конструкций будет описываться математически линейными системами, с этой точки зрения принцип независимости действия сил есть не что иное, как хорошо знакомый принцип суперпозиции.

3 . Принцип Сен-Венана.

Способ приложения нагрузки не сказывается в точках, достаточно удаленных от места приложения нагрузки. Например, две совершенно одинаковых консольных балки нагружены одной и той же по величине силой , но в первом случае эта сила есть давление опирающейся на данную балку другой балки, а во втором случае к балке через проушину подвешен груз . Ясно, что характер распределения напряжений в месте нагружения здесь будет совершенно различным, но в сечениях достаточно удаленных от места приложения, нагрузки индивидуальные особенности передачи нагрузки сказываться не будут.

Принцип Сен-Венана дает возможность заменять действующие силы системами статически эквивалентными. Это позволяет схематизировать силы, действующие на конструкцию.

В частности, системы статически эквивалентные нулю вызывают напряжения лишь в локальной области. Например, полоса сжата клещами. В этом случае возникают только местные напряжения.

П ринцип Сен-Венана имеет ограниченное применение для тонкостенных стержней.