Изгиб с кручением. Расчетные формулы по различным теориям предельного напряженного состояния.

Одним из наиболее частых нагружений в машиностроительной практике является совместное воздействие изгиба и кручения. В таких условиях например работают валы редукторов.

П риводя силы, действующие на вал к оси вала, имеем следующую расчетную схему.

На участке АВ вал будет работать на изгиб с кручением. Очевидно, что наиболее опасным будет сечение В.

Наибольшие нормальные напряжения, возникающие в этом сечении

Наибольшие касательные напряжения

В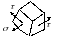 наиболее опасной точке будет возникать плоское напряженное состояние

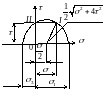
В качестве примера мы рассматривали круглое напряженное состояние, но такой же характер напряженного состояния будет при любом поперечном сечении и последующие результаты применимы для произвольных сечений.

Найдем главные напряжения

;

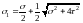Подставляя найденные главные напряжения в выражения для по различным теориям

1. Теория наибольших касательных напряжений

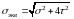
2. Теория энергии формоизменения

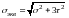
3. Теория Мора

Эти формулы можно использовать не только для изгиба, но и для растяжения (сжатия), изгиба и кручения.

В случае изгиба с кручением круглых валов, учитывая, что

получим

Устойчивость сжатых стержней Понятие устойчивости равновесного состояния деформируемой системы.

Не все теоретически возможные равновесные формы могут быть реализованы в действительности. Реальный объект всегда отличается от расчетной схемы. Всегда имеются неучтенные в расчетной схеме силы, реальная геометрическая форма всегда отклоняется от проектной. Имеются отклонения в свойствах материалов от того, что предусматривалось проектом и т. д. В некоторых случаях эти, казалось бы второстепенные факторы могут привести к тому, что теоретически возможное состояние практически становится неустойчивым.

Н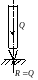 апример, никто не видел следующей картины: идеально прямой карандаш стоит строго вертикально на горизонтальном идеально гладком стекле. В этом случае реакция опорной поверхности направлена строго вертикально и равняется весу карандаша. Две равные по величине действующие по одной прямой и направленные в противоположные стороны силы, должны уравновешиваться, однако данное равновесное состояние реализовать в действительности невозможно. Помимо веса карандаша и реакции поверхности будут действовать и другие силы, например силы обусловленные движением воздуха, карандаш не будут строго прямолинейным, а поверхность стекла совершенно горизонтальной и идеально гладкой и т. д.

Будем называть неучтенные силы, отклонения в геометрической форме и т. д., возмущениями.

Определение: будем называть равновесное состояние устойчивым, если оно мало изменяется при малых возмущениях.

Приведем некоторые примеры.

1 . Тяжелый шар на поверхности, имеющий вершины, впадины и горизонтальные участки.

В том случае, когда шарик находится на вершине составляющая силы тяжести Т, возникающая при его отклонении, уводит его от первоначального состояния, для шарика, находящегося во впадине сила Т будет возвращать отклоненный шарик в первоначальное состояние и он будет колебаться в окрестности наиболее низкой точки впадины, т. е. при малых отклонениях состояние шарика будет также меняться мало. Случай шарика, находящегося на горизонтальной поверхности, будет случаем, разграничивающим рассмотренные выше неустойчивые и устойчивые равновесные состояния.

Такое состояние называется безразличным

2 . Картину разрушения образца при растяжении с образованием шейки можно характеризовать, как потерю устойчивости цилиндрической формы образца.

По мере приближения состояния образца к точке С цилиндрическая форма образца становится неустойчивой, образуется шейка и малым изменениям силы соответствуют значительные изменения конфигурации системы.

3. Центрально сжатый гибкий стержень

П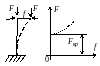 редполагается, что стержень идеально прямой, а сила приложена строго по оси (что, конечно, практически невозможно). Для того, чтобы судить устойчиво ли данное равновесное состояние, надо приложить горизонтальную возмущающую силу, которая вызовет прогиб. Если сила F невелика, то прогиб окажется малым, равновесное состояние (прямолинейное) практически не изменится.

Однако, если сила F превысит некоторое значение называющееся критическим 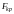, то равновесное состояние становится неустойчивым, т. е. любые малые возмущения приведут к значительным прогибам. Зависимость между силами и прогибом показана на рисунке. Пунктирной линией показано действительное поведение стержня, которое можно обнаружить с помощью нелинейных решений, сплошной чертой показано грубое, линейное решение задачи.