График выборочной (синий) и теоретической (оранжевый) функций распределения
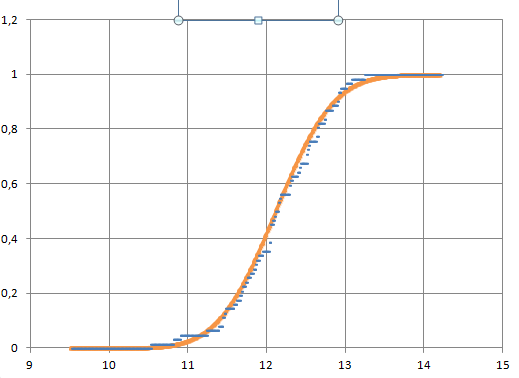
Рис. 1
f(R6) – плотность распределения. Функция задается с помощью функции НОРМРАСПР, (в строке Интегральная – 0).
График теоретической плотности распределения
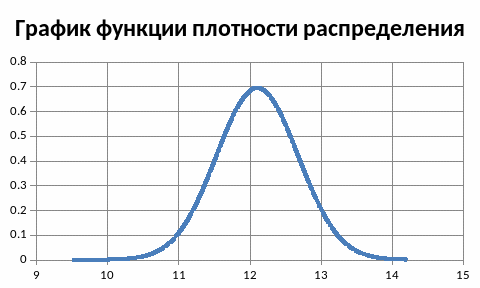
Для построения гистограммы воспользуемся пакетом анализа→ гистограмма
Карман - середины интервалов группировки.
Интегральный процент – накопленные частоты в процентах.
Частота - количество выборочных значений, которые попали данный интервал (карман).
Шаг – постоянная величина, равная разности двух соседних карманов.
Относительная частота – отношение частоты к числу элементов выборки.
Приведенная частота –отношение относительной частоты к шагу.
На основе полученного анализа строит гистограмму приведенных частот
Гистограмма относительных частот
Рис.3
Создаём: листРегрессионный анализ.
Регрессионный анализ заключается в определения аналитического выражения связи зависимости случайной величины Y с независимыми случайными величинами X1, X2, X3…Xn. Форма связи результативного признака Y с факторами X1, X2, X3…Xn получила название уравнение регрессии.
Форма связи результативного признака Y с факторами выбранного уравнения различают линейную и нелинейную регрессию. В зависимости от числа выбранных признаков различают парную и множественную регрессию.
Пусть у нас есть случайные величины сопротивления и ток. Предположим, что между этими величинами существует статистическая линейная зависимость. Составим уравнение множественной регрессии:
