25. Нахождение входного и выходного зрачков.

Апертурная диафрагма - диафрагма, ограничивающая пучок лучей, выходящих из осевой точки предмета, и тем самым определяющая освещённость изображения. Входной зрачок - параксиальной изображение апертурной диафрагмы в обратном ходе лучей через предшествующие части оптической системы или апертурная диафрагма, расположенная в пространстве предметов. Выходной зрачок - изображение апертурной диафрагмы в прямом ходе лучей через последующие части оптической системы или апертурная диафрагма в пространстве изображений.

26. М етоды определения направления изменения коррекционных параметров.

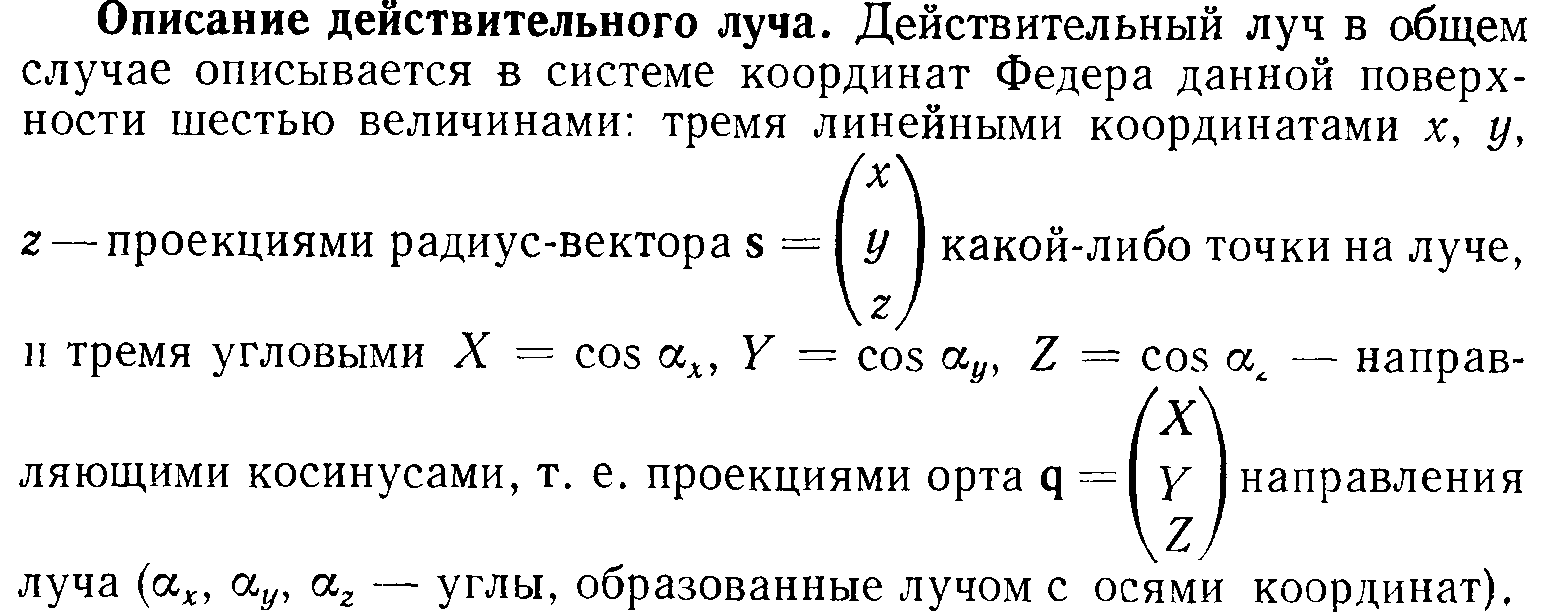
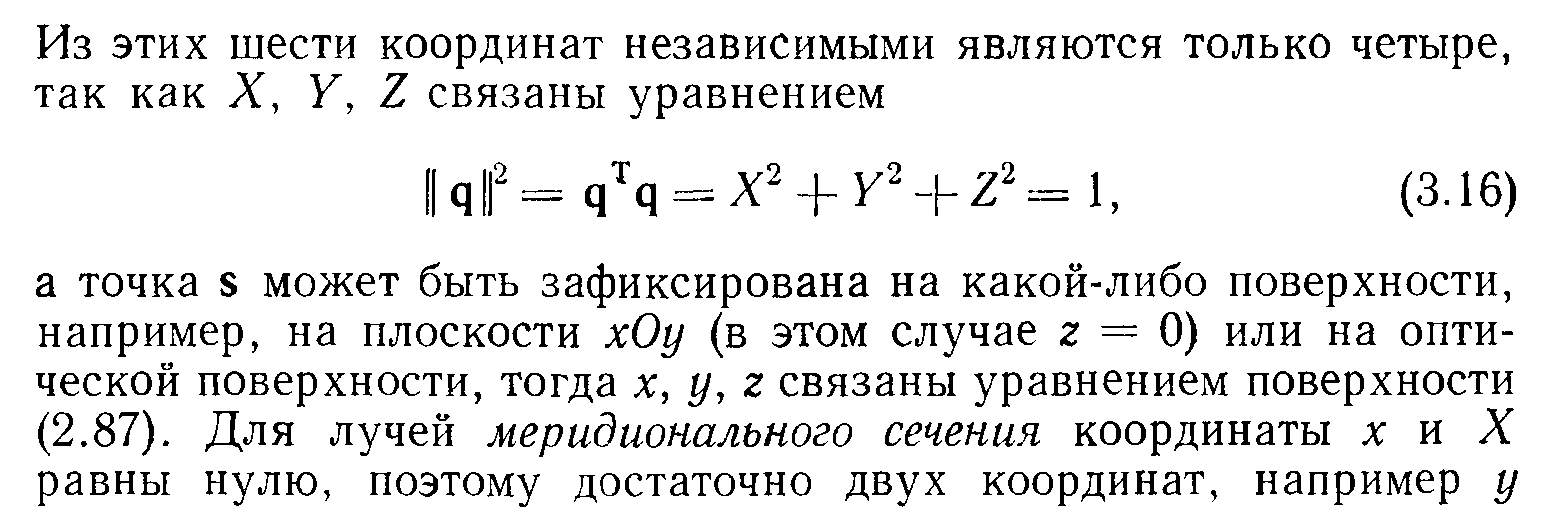
27. З 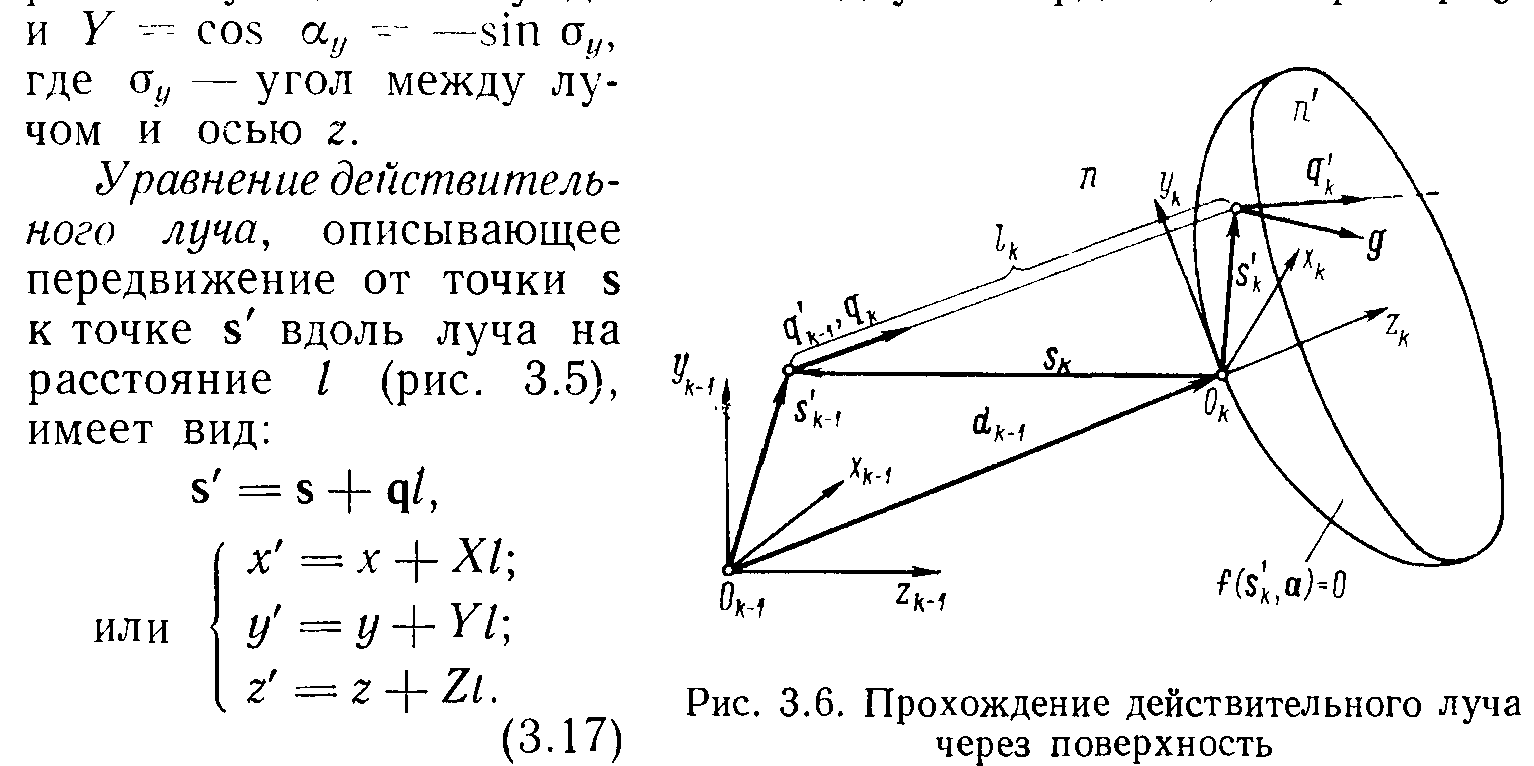адание исходных данных для расчета действительных лучей.

28. Способ вычисление производных

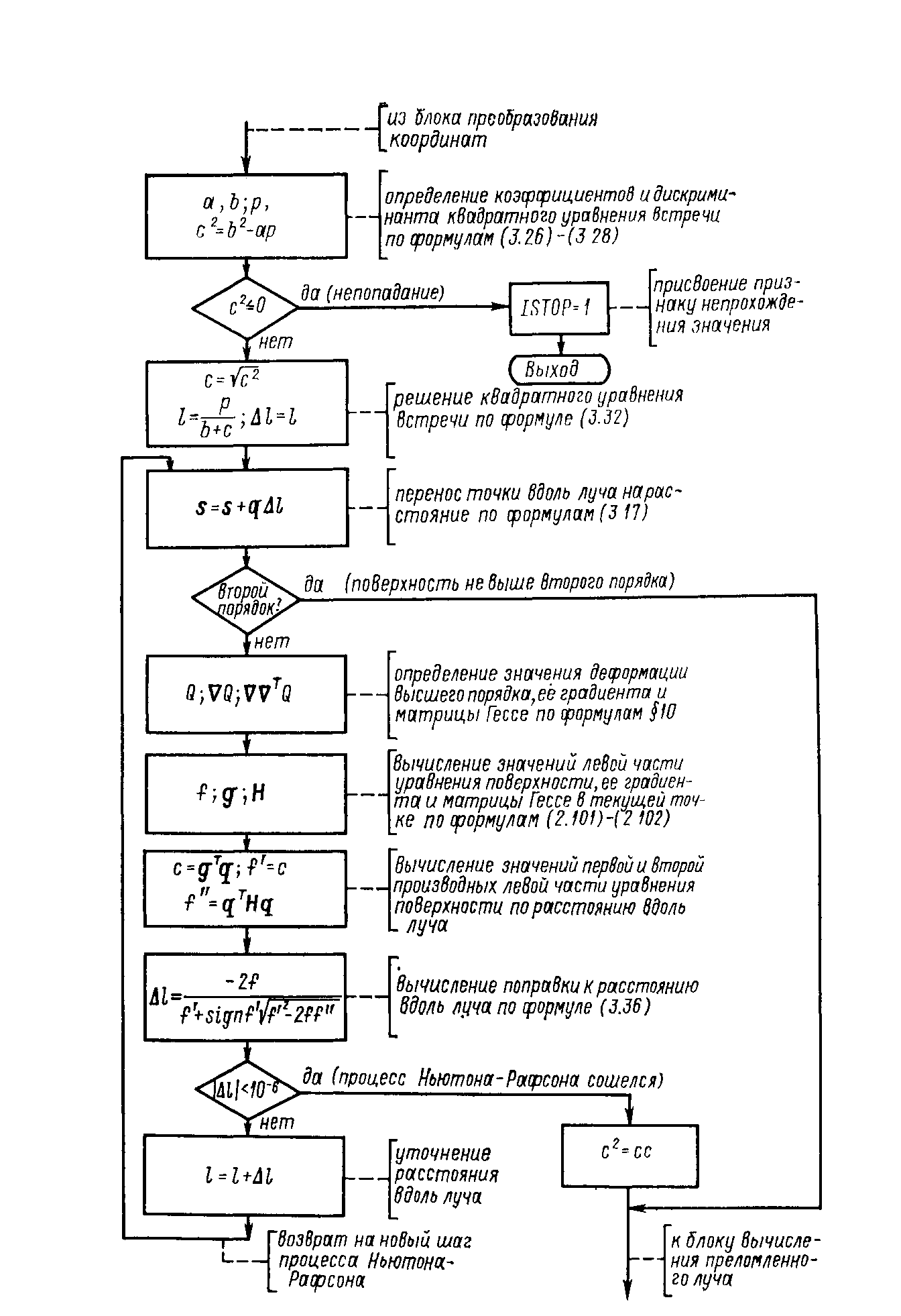
29. Алгоритм расчета действительных лучей. Основной объем информации об аберрациях оптической системы в процессе ее анализа получают из расчета действительных лучей, идущих на произвольно большом расстоянии от оптической оси и соответствующих ходу реальных физических лучей — нормалей к волновым фронтам.

30. В ычисление допусков на ОС.

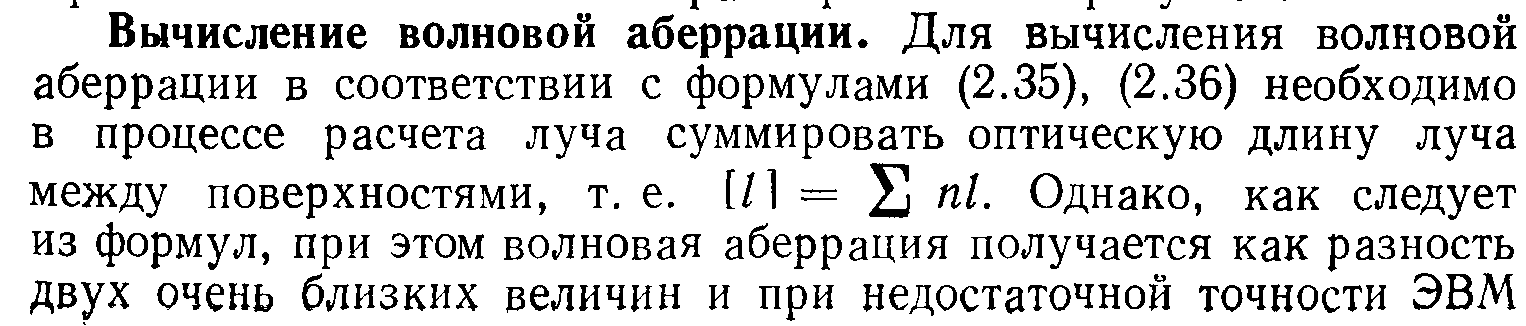
31. В ычисление аберраций.

32. Т аблица влияния.

33. Качество изображения ОС.

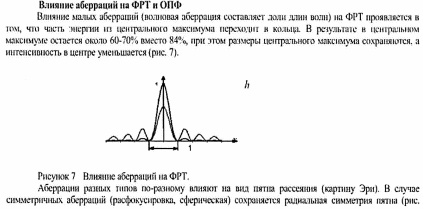
34. Программы автоматизированного расчета ОС.

35. Описание асферических поверхностей.

    

36. Методы поиска минимума оценочной функции.

37. А нализ структуры изображения в геометрическом приближении.

38. Перерасчет на плавки стекол.

39. Результаты расчета действительных лучей.

40. Связанные параметры при оптимизации.

Метод Ньютона

Р ассматриваемые методы относятся к методам второго порядка. Они основаны на представлении оценочной функции в виде квадратичной формы, которая, в свою очередь, получается из линейной модели оптимизируемых функций, выраженной формулой Направление спуска в ньютоновских методах указывает прямо на минимум линейной модели, поэтому они имеют обычно значительно лучшую сходимость, чем градиентные методы. Ха- рактерной их особенностью является необходимость решения на каждом шаге системы линейных уравнений. Название методов взято по аналогии с методом Ньютона—Рафсона уточнения корня нелинейного уравнения (см. § 14). В том и другом случае мы за- меняем на каждом шаге нелинейное уравнение или нелинейную систему уравнений E.5) ее линейной моделью. По той же причине эти методы называют также методами линеаризации.

Метод наименьших квадратов.

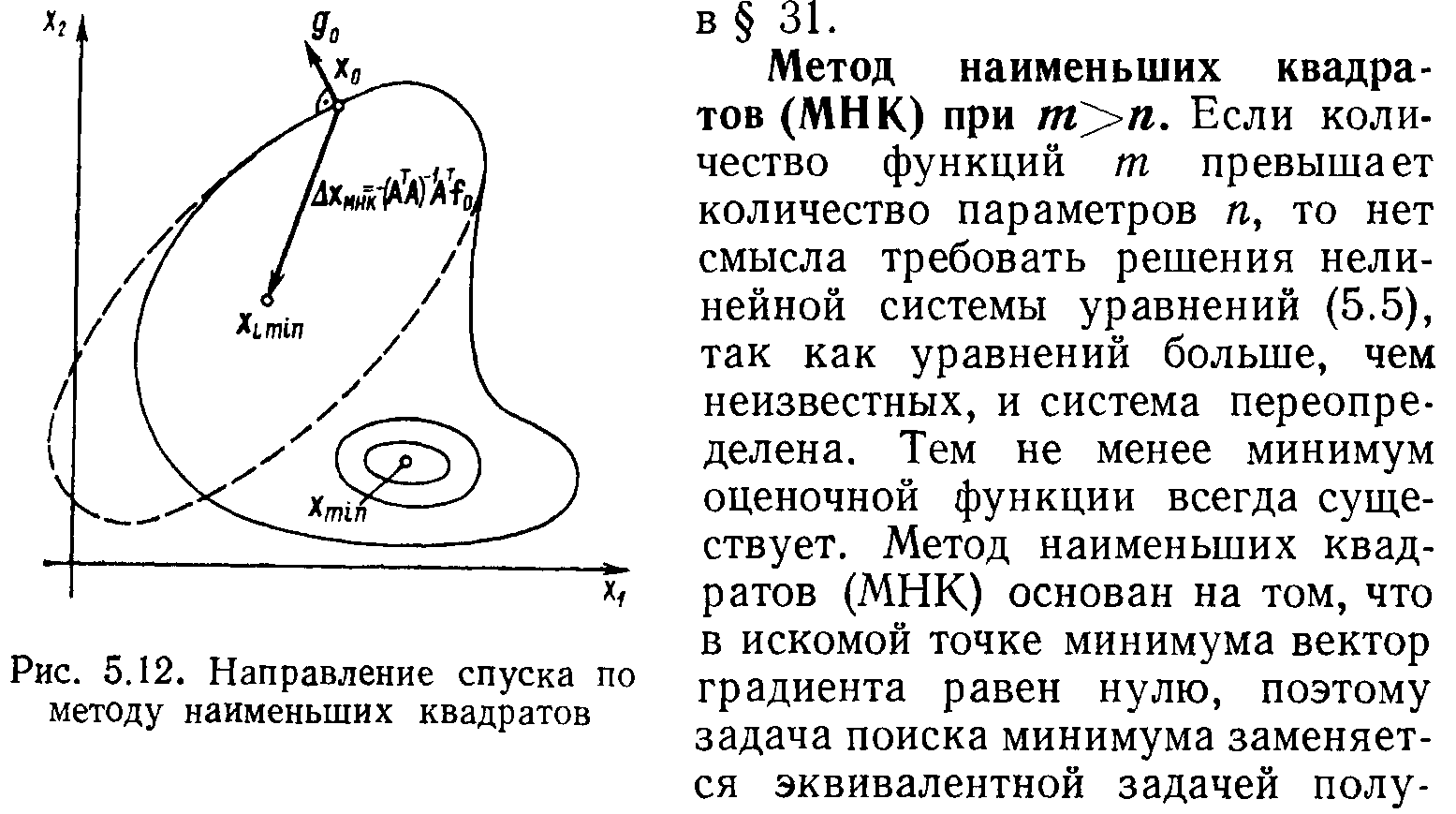
+ Посмотреть методы обработки оценочной функции: метод Ньютона, демпфированный метод наименьших квадратов, метод Лагранджа (книга Родионов С. А.)