
- •Задание оптических сред.
- •Блочно-иерархический подход к проектированию ос.
- •З адание оптических поверхностей.
- •Методы автоматизированного проектирования ос.
- •К онструктивные параметры ос.
- •З адание оптических поверхностей и диафрагм.
- •Типы асферических поверхностей и их задание.
- •Задание воздушных промежутков и внешних параметров ос.
- •А лгоритм синтеза ос.
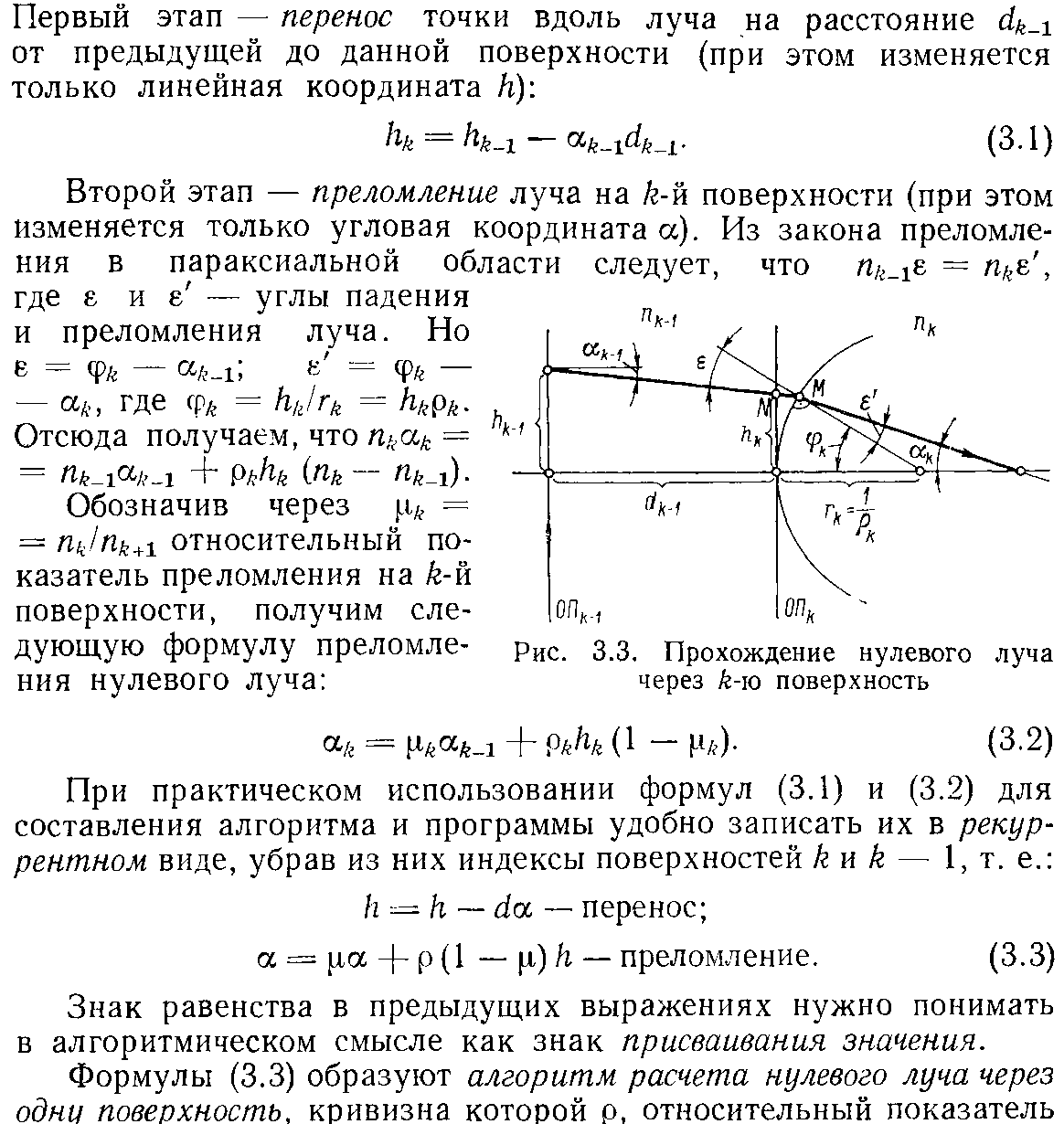
- •О писание ос в параксиальной области.
- •В ычисление оптических величин в параксиальной области.
- •Связанные параметры.
- •Вычисление поверхностных коэффициентов и аберраций III порядка
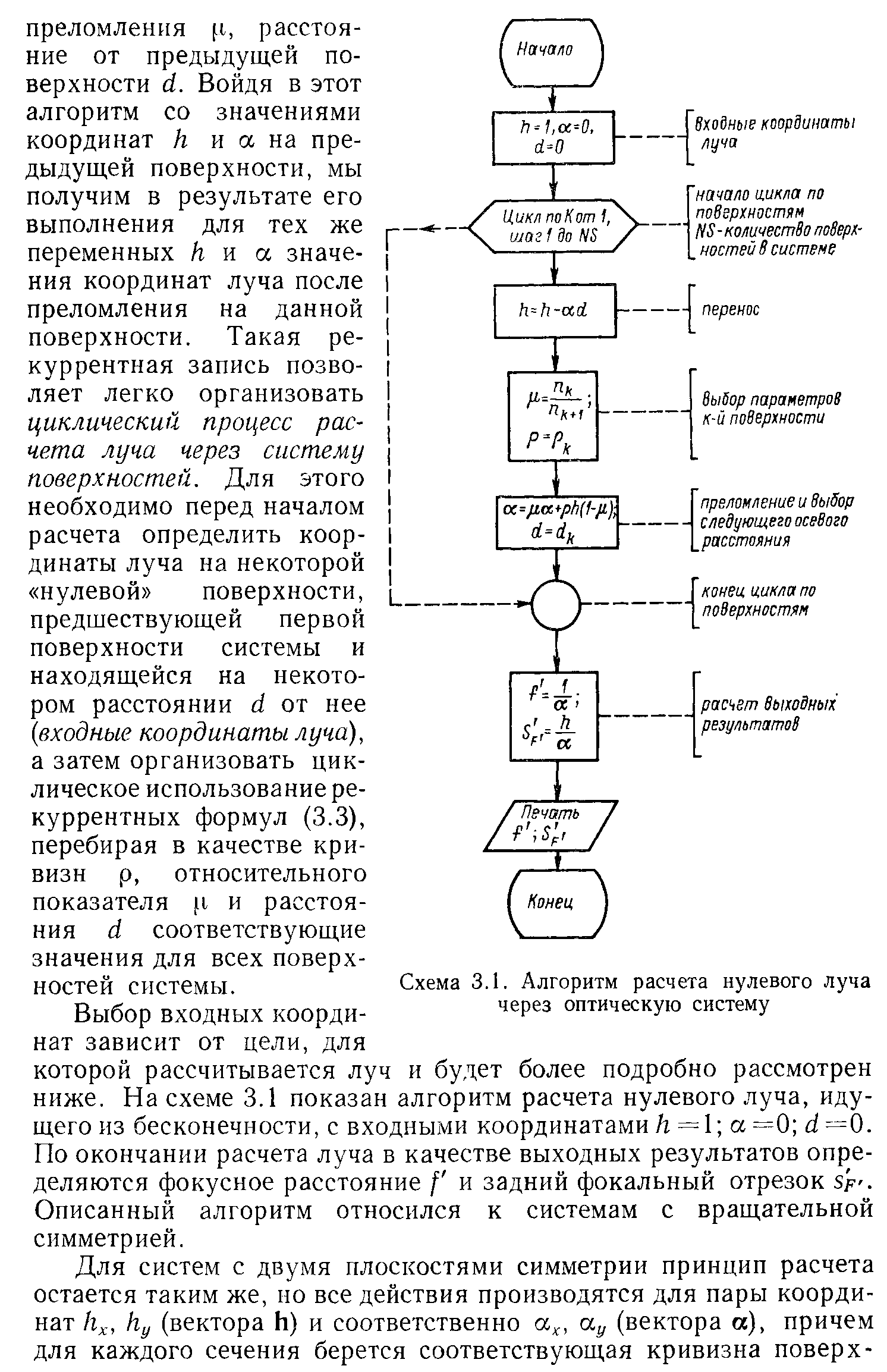
- •З адание исходных данных для расчета нулевых лучей.
- •Нахождение входного и выходного зрачков.
В ычисление оптических величин в параксиальной области.





Связанные параметры.
Вычисление поверхностных коэффициентов и аберраций III порядка
Оптимизируемые функции Целью оптимизации является достижение наилучшего качества оптимизируемой системы. Пусть мы имеем некоторый набор характеристик
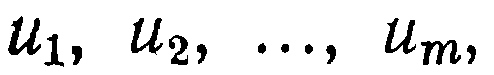 определяющий это качество. В него могут
входить самые разнообразные характеристики,
например, увеличение, задний отрезок,
положения зрачков, аберрации в том или
ином представлении, характеристики
качества изображения и другие, а также
различные их комбинации. Характеристики
имеют различный физический смысл,
размерность и различные цели оптимизации,
причем одни необходимо приблизить к
заданным значениям, другие сделать как
можно меньшими или как можно большими
по абсолютной величине. Для того чтобы
придать им более однородный и удобный
для оптимизации вид, преобразуем все
характеристики следующим образом.
Во-первых, приведем их к такому виду,
чтобы целью оптимизации во всех случаях
было бы получение как можно более
близких к нулю значений, во-вторых,
поделим все характеристики на некоторое
масштабы, имеющие ту же физическую
размерность. В результате получим
безразмерные нормированные величины
— оптимизируемые функции fi
в виде
определяющий это качество. В него могут
входить самые разнообразные характеристики,
например, увеличение, задний отрезок,
положения зрачков, аберрации в том или
ином представлении, характеристики
качества изображения и другие, а также
различные их комбинации. Характеристики
имеют различный физический смысл,
размерность и различные цели оптимизации,
причем одни необходимо приблизить к
заданным значениям, другие сделать как
можно меньшими или как можно большими
по абсолютной величине. Для того чтобы
придать им более однородный и удобный
для оптимизации вид, преобразуем все
характеристики следующим образом.
Во-первых, приведем их к такому виду,
чтобы целью оптимизации во всех случаях
было бы получение как можно более
близких к нулю значений, во-вторых,
поделим все характеристики на некоторое
масштабы, имеющие ту же физическую
размерность. В результате получим
безразмерные нормированные величины
— оптимизируемые функции fi
в виде
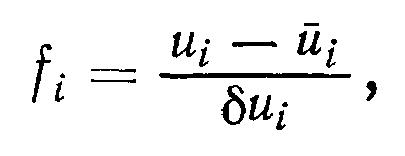
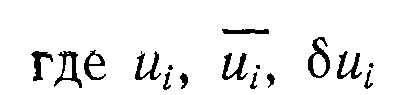 текущее значение, заданное значение и
масштаб какой-либо характеристики
(если щ должны принимать, как можно
большие по модулю значения, то вместо
них можно взять обратные величины Выбор
масштабов дельта у преследует цель не
только сделать все функции безразмерными
и однородными по содержанию, но и придает
тот или иной вес данной функции в общем
наборе. Чем меньше масштаб, тем больше
функция и тем больший вес она имеет в
процессе оптимизации. Следовательно,
назначение масштабов может существенным
образом повлиять на ход и результат
оптимизации.
текущее значение, заданное значение и
масштаб какой-либо характеристики
(если щ должны принимать, как можно
большие по модулю значения, то вместо
них можно взять обратные величины Выбор
масштабов дельта у преследует цель не
только сделать все функции безразмерными
и однородными по содержанию, но и придает
тот или иной вес данной функции в общем
наборе. Чем меньше масштаб, тем больше
функция и тем больший вес она имеет в
процессе оптимизации. Следовательно,
назначение масштабов может существенным
образом повлиять на ход и результат
оптимизации.
З адание исходных данных для расчета нулевых лучей.
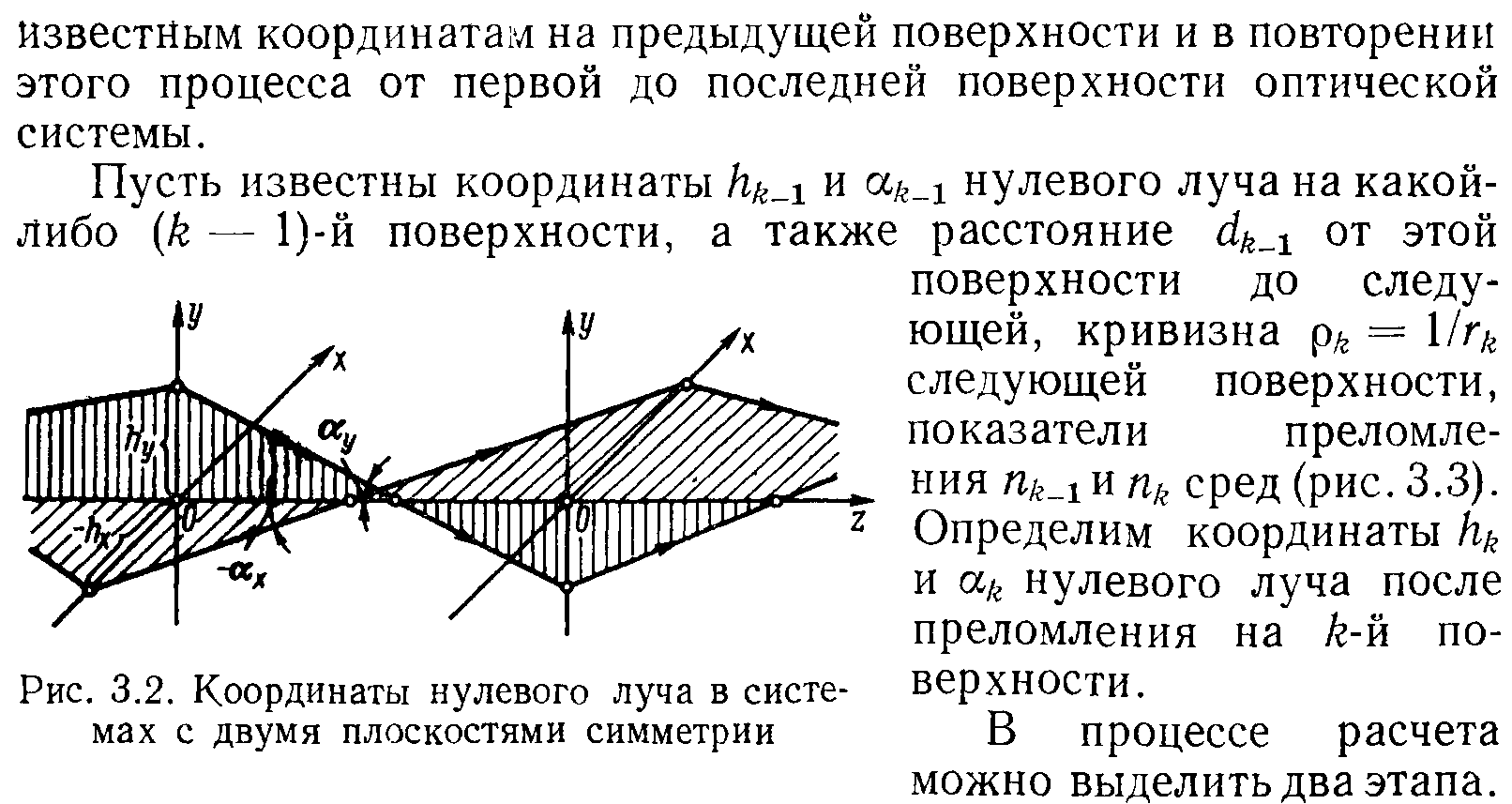
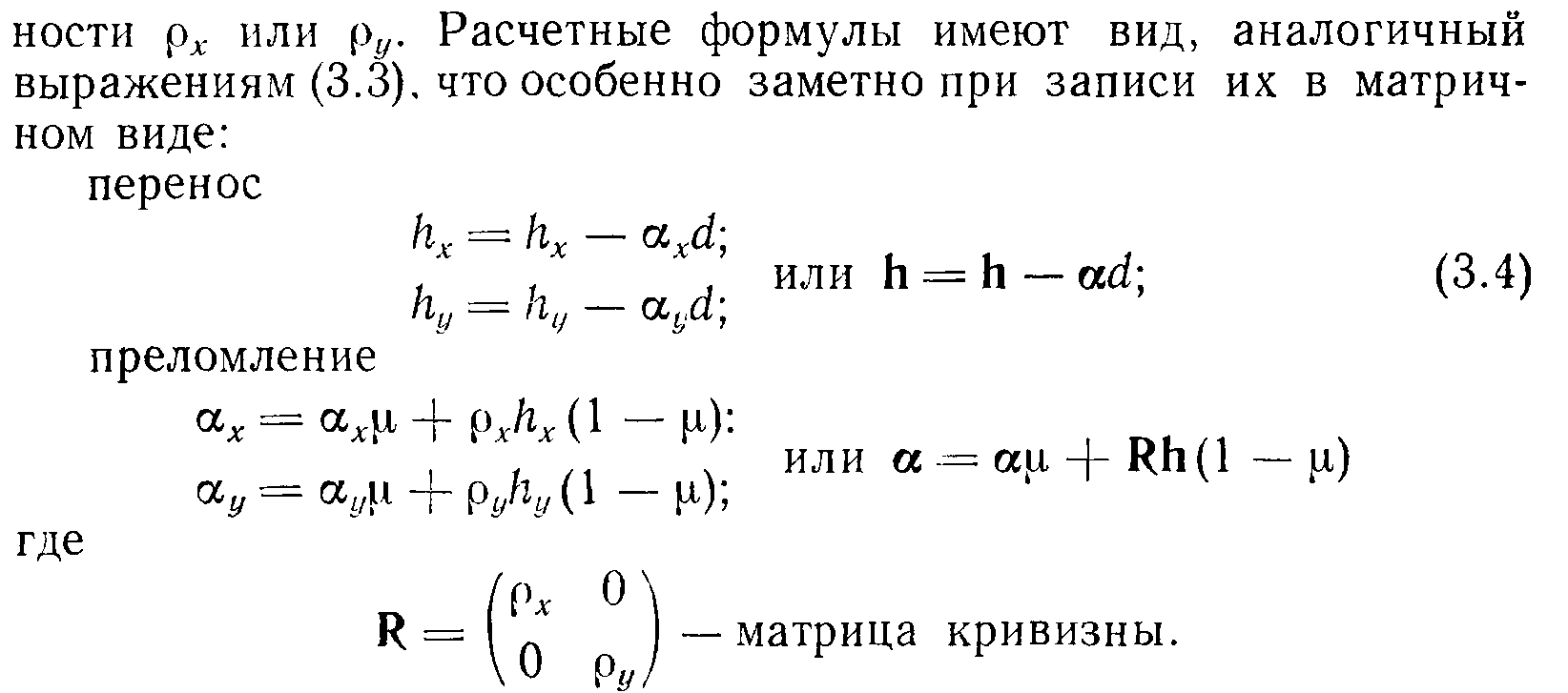
О
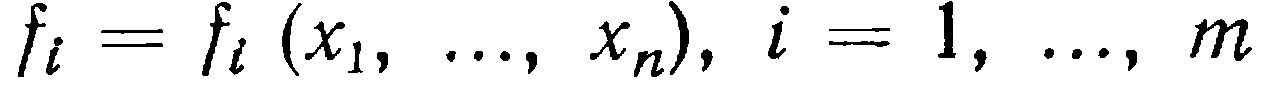
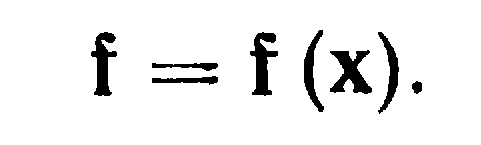 ценочная
функция.
Так
же, как и параметры, объединим все
функции в т-мерный вектор f. Как следует
из сказанного выше, все функции зависят
от параметров xi
т. е.
ценочная
функция.
Так
же, как и параметры, объединим все
функции в т-мерный вектор f. Как следует
из сказанного выше, все функции зависят
от параметров xi
т. е.
или в матричном (векторном) виде
Будем считать, что эти зависимости являются однозначными и непрерывными. Отметим, что по своему характеру они в общем случае нелинейны. Если бы все функции /> линейно зависели от всех параметров xh то задача оптимизации решалась бы тривиально. Чем более нелинейны зависимости f (x), тем сложнее оптимизация. Если бы заранее было известно, что существует точка в пространстве параметров, в которой вектор функций равен нулю, то задача оптимизации свелась бы к поиску этой точки, т. е. к решению системы нелинейных уравнений,
f![]() (x)
= o.
В большинстве случаев, однако, нельзя
заранее гарантировать существование
этого решения. В таком случае задача
его поиска некорректна. Также некорректно
требование нахождения всех функций в
заданных интервалах,
определяемых величиной допусков
(x)
= o.
В большинстве случаев, однако, нельзя
заранее гарантировать существование
этого решения. В таком случае задача
его поиска некорректна. Также некорректно
требование нахождения всех функций в
заданных интервалах,
определяемых величиной допусков
т. е. задача решения системы нелинейных неравенств
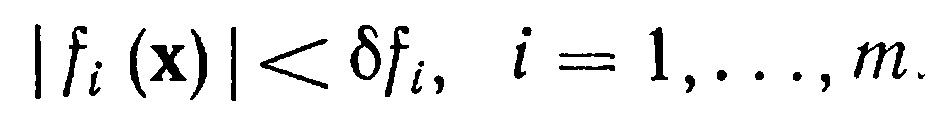
Более общий характер имеет задача поиска в пространстве параметров точки, в которой вектор функций ближе всего к нулю. Такая точка всегда существует и поэтому постановка задачи корректна, но при этом нам необходимо ввести критерий близости вектора f к нулю. Этот критерий в оптимизации называется оценочной или целевой функцией.
