О писание ос в параксиальной области.

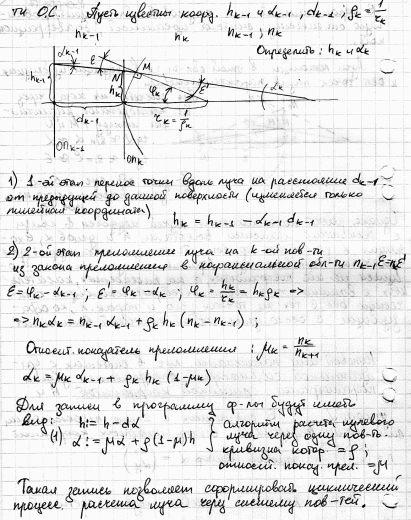
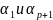
П араметры оптимизации. Оптимизационная модель ОС — это совокупность математических понятий, описывающих ее как объект оптимизации, а также соотношений, связывающих эти понятия. Основные компоненты: параметры оптимизации, оптимизируемые функции, критерий оптимизации, ограничения и связывающие их соотношения – проба и проба производных. Параметры оптимизации (это не конструктивные параметры!): 1). Не все конструктивные параметры изменяются; 2). Используют величины связанные с ними (углы нулевого луча); 3). Несколько конструктивных параметров могут быть связаны между собой; 4). Конструктивные параметры имеют различные физические величины. Параметры оптимизации – некоторые безразмерные величины, которым можно в процессе оптимизации придавать любые значения, однозначно определяющие конструкцию ОС. Безразмерность достигается делением соответствующих конструктивных параметров на свои масштабы. Для оптимизации параметры объединяют в вектор параметров х Элементы вектора рассматриваются как координаты точки в n-мерном пространстве параметров → каждой конструкции ОС соответствует определенная точка в пространстве и наоборот. При выборе параметров оптимизации необходимо стремиться к тому, чтобы оптимизируемые характеристики зависели как можно более линейно, т.к. сходимость оптимизации максимальна. Для некоторых методов оптимизации желательно, чтобы параметры были разделены. В качестве параметров чаще берут кривизну поверхности , коэффициенты асферических поверхностей , осевые расстояния . Иногда вместо используют (нулевой луч с осью) т.к. по известным и заданной можно найти Применение не включают в опт.! и некоторые промежуточные углы 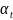при оптимизации позволяет сохранять заданное (при ), увеличение (при 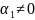) телескопичность системы т т.д. небольшая разность в углах и приводит к большим изменениям (при близких значениях 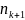и 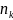или малых ) → и в таких случаях зависимы. Параметром оптимизации можно брать расстояние до АД и задний отрезок (положение плоскости наилучшей установки). Если брать , то принимают за параметр оптимизации коэффициент разложения его показателя по ортогональному базису. В этом случае k-того стекла - полиномы, ортогональные на отрезке (-1,1) с весом 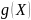. Однако такая оптимизация сложна т.к. в реальных конструкциях ( ) могут принимать значения из ограниченного набора, определяемого каталогом стекла. Т.е. при оптимизации необходимо всегда накладывать ограничения.