- •Задание оптических сред.
- •Блочно-иерархический подход к проектированию ос.
- •З адание оптических поверхностей.
- •Методы автоматизированного проектирования ос.
- •К онструктивные параметры ос.
- •З адание оптических поверхностей и диафрагм.
- •Типы асферических поверхностей и их задание.
- •Задание воздушных промежутков и внешних параметров ос.
- •А лгоритм синтеза ос.
- •О писание ос в параксиальной области.
- •В ычисление оптических величин в параксиальной области.
- •Связанные параметры.
- •Вычисление поверхностных коэффициентов и аберраций III порядка
- •З адание исходных данных для расчета нулевых лучей.
- •Нахождение входного и выходного зрачков.
Математические модели ОС. Математические модели оптической системы, как и любого другого объекта проектирования, должны быть: адекватными, т. е. описывать свойства объекта с необходимой точностью; универсальными, т. е. пригодными для широкого класса объектов; экономичными, требующими минимального количества вычислений при обработке, а также простыми и наглядными для исполь- зования. Никакая единая модель не может удовлетворить всем этим требованиям, поэтому используется система моделей, основанная на блочно-иерархическом подходе к описанию и проектированию объекта. Процесс проектирования при этом разбивается на несколько иерархических уровней, на каждом из которых рассматриваются системы, состоящие из небольшого, легко обозримого числа элементов, представляемых в свою очередь как системы на низших уровнях. При проектировании оптических систем можно выделить три иерархических уровня. На высшем уровне оптическая система рассматривается как элемент в цепи различных устройств, входящих в оптический прибор и функционирующих совместно. На этом уровне используется внешняя функциональная модель, описывающая оптическую систему безотносительно к физическим принципам ее работы, т. е. как преобразователь сигналов общего вида. Характеристики и понятия этой модели (внешние характеристики оптической системы) являются поэтому объектно-независимыми, применимыми к любым преобразователям, работающим вместе с оптической системой. В процессе проектирования на этом уровне определяются значения внешних характеристик всех элементов, в том числе и оптической системы, обеспечивающие оптимальное функ- ционирование оптического прибора в целом. На среднем уровне оптическая система представляется состоящей из элементов. В зависимости от степени детализации рассмотрения средний уровень в свою очередь можно разбить на несколько подуровней. На высшем из них в качестве элементов выступают узлы, имеющие самостоятельное значение (например, объективы, окуляры, оборачивающие системы), на среднем — компоненты с известными аберрационными свойствами, на низшем — оптические поверхности и среды. Задачей проектирования на этом уровне является определение значений конструктивных параметров, обеспечивающих требуемые значения внешних характеристик, полученных на высшем уровне. Здесь используются две математические модели. Внутренняя функциональная модель отражает физические принципы формирования оптического изображения. Основным понятием этой модели является зрачковая функция, показывающая влияние оптической системы на проходящее через нее электромагнитное поле. Харак- теристики и понятия этой модели (внутренние характеристики оптической системы) являются объектно-ориентированными и пригодными для описания только оптических систем. Принципиальная конструкционная модель включает в себя конструктивные параметры, определяющие функционирование оптической системы — параметры оптических сред, поверхностей и их взаимного расположения. Указанные модели, рассмотренные подробно в гл. 2, объединены системой обобщенных характеристику позволяющей удовлетворить требованиям адекватности, универсальности, экономичности и простоты моделей. На низшем уровне проектирования оптическая система представляется в виде совокупности оптических деталей, закрепленных в оправах; здесь определяются конструктивные элементы, обеспечивающие надежное закрепление деталей и расположение их друг относительно друга с необходимой точностью. На этом уровне используется детальная конструкционная модель оптической системы, включающая в себя математическое описание крепежных элементов, взаимного расположения и подвижек деталей и т. п. Кроме рассмотренных моделей, из которых каждая является специфической для своего уровня проектирования, необходимо рассмотреть математические модели, обладающие общими чертами и использующиеся на любом уровне. Оптимизационная модель описывает оптическую систему как объект оптимизации. Она включает в себя характеристики оптической системы, которые мы хотим улучшить (оптимизировать) на данном уровне; параметры, изменением которых мы производим оптимизацию; ограничения на область возможных изменений и математические соотношения, связывающие параметры и характеристики. Статистическая модель характеризует оптическую систему как объект, полученный в процессе изготовления и сборки деталей. В силу неизбежных технологических погрешностей, носящих случайный характер, конструктивные параметры и характеристики оптической системы становятся случайными величинами, законы распределения которых и описываются при помощи статистической модели. Эта модель, рас- смотренная в гл. 6, необходима при определении допусков на технологические погрешности.
О
 ценка
качества изображения. Пограничная
кривая.
Тест-объект
"полуплоскость".
Этот тест-объект
материализуется
в виде прямолинейного края непрозрачной
заслонки (лезвия) на освещенном фоне.
При необходимости характеризовать
резкость деталей изображения,
создаваемого исследуемой системой,
рассматривают структуру изображения
тест-объекта, представляющего собой
прямолинейную границу черного и светлого
полей, так называемого пограничного
теста или полуплоскости. Функция,
описывающая распределение яркости
в тест-объекте "полуплоскость"
(рис.10), есть квазиодномерная функция
скачка.
Изображение
тест-объекта "полуплоскость"
есть пятно рассеяния в форме более
или менее размытого изображения
края. Функция, описывающая распределение
освещенности в изображении тест-объекта
“полуплоскость” есть двумерная
(квазиодномерная) функция края или
“краевая (переходная) функция” (рис.
11); ее график называется "пограничная
кривая". Резкость изображения
характеризуется степенью наклона
пограничной кривой. В то же время наклон
пограничной кривой зависит от структуры
пятна рассеяния. Чем более размыто
пятно рассеяния, тем больше наклон
пограничной кривой и хуже резкость
изображения. Тест-объект "полуплоскость"
описывает часто встречающиеся в
оптической измерительной практике
объекты: например, край непрозрачного
объекта на освещенном фоне, на который
выполняются оптические измерительные
наводки.
ценка
качества изображения. Пограничная
кривая.
Тест-объект
"полуплоскость".
Этот тест-объект
материализуется
в виде прямолинейного края непрозрачной
заслонки (лезвия) на освещенном фоне.
При необходимости характеризовать
резкость деталей изображения,
создаваемого исследуемой системой,
рассматривают структуру изображения
тест-объекта, представляющего собой
прямолинейную границу черного и светлого
полей, так называемого пограничного
теста или полуплоскости. Функция,
описывающая распределение яркости
в тест-объекте "полуплоскость"
(рис.10), есть квазиодномерная функция
скачка.
Изображение
тест-объекта "полуплоскость"
есть пятно рассеяния в форме более
или менее размытого изображения
края. Функция, описывающая распределение
освещенности в изображении тест-объекта
“полуплоскость” есть двумерная
(квазиодномерная) функция края или
“краевая (переходная) функция” (рис.
11); ее график называется "пограничная
кривая". Резкость изображения
характеризуется степенью наклона
пограничной кривой. В то же время наклон
пограничной кривой зависит от структуры
пятна рассеяния. Чем более размыто
пятно рассеяния, тем больше наклон
пограничной кривой и хуже резкость
изображения. Тест-объект "полуплоскость"
описывает часто встречающиеся в
оптической измерительной практике
объекты: например, край непрозрачного
объекта на освещенном фоне, на который
выполняются оптические измерительные
наводки.
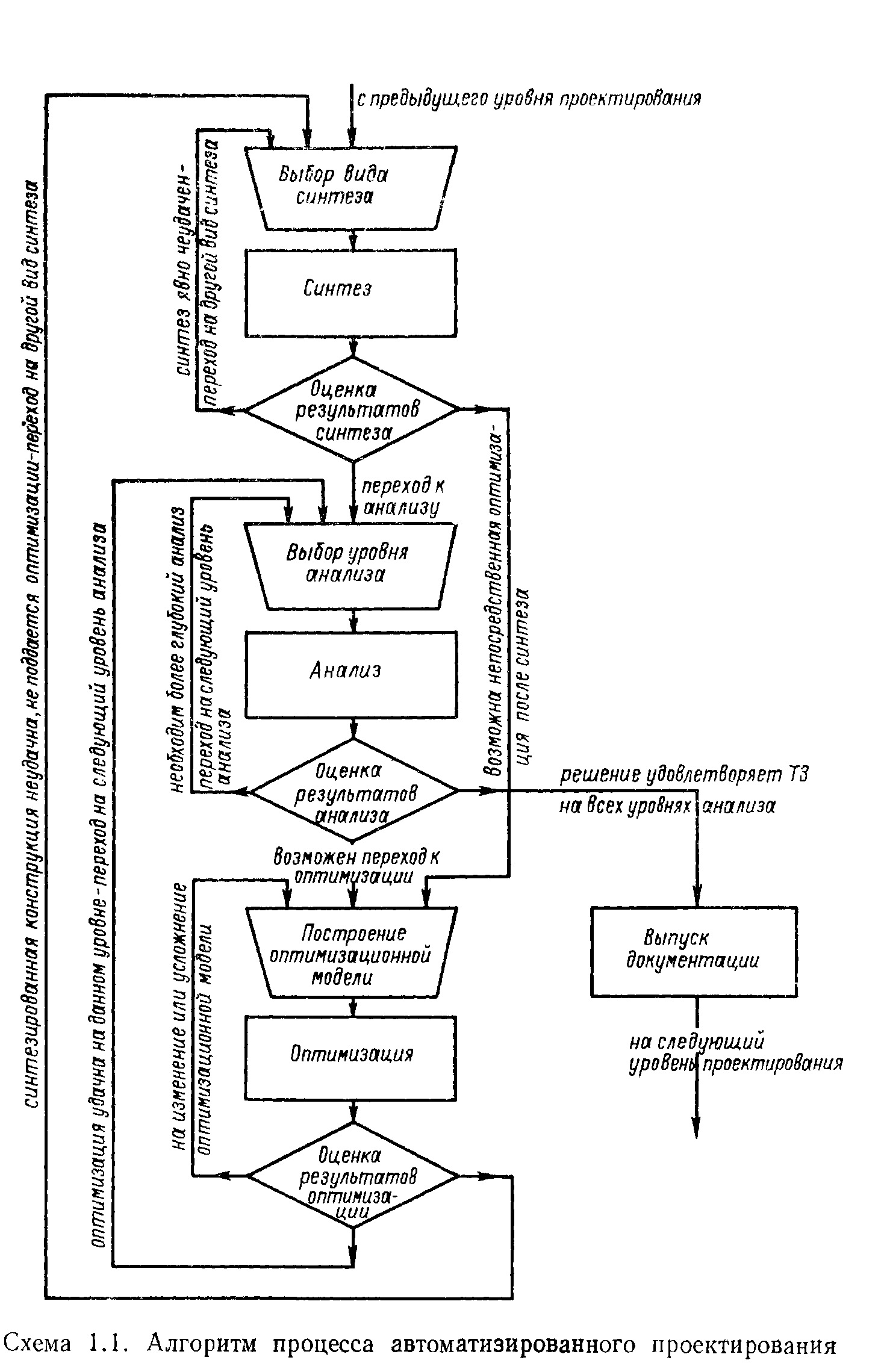
Операции, производимые над математическими моделями ОС. Процесс проектирования на любом иерархическом уровне можно представить в виде последовательности следующих типовых операций: анализа, синтеза и оптимизации. Под анализом (прямая задача) будем понимать вычисление значений характеристик по известным значениям параметров. Если все параметры объединить в вектор х, а характеристики — в вектор f; то условная схема анализа будет выглядеть так, как показано на рис. 1.1. Анализ является детерминированной и объектно-ориентированной операцией. На среднем уровне проектирования анализ состоит в определении внутренних характеристик оптической системы по известным значениям конструктивных параметров. Здесь можно выделить различные подуровни, отличающиеся степенью полноты и трудоемкостью: анализ в гауссовой и зейделевой областях (определение параксиальных характеристик и аберраций третьего порядка), вычисление аберраций небольшого количества действительных лучей, определение габаритов пучков и, наконец, аппроксимация аберраций и формирование внутренней функциональной модели. Основное содержание этих уровней анализа составляет расчет хода лучей через оптическую систему, рассмотренный в гл. 3. Следующий уровень анализа, на котором входными данными х являются внутренние характеристики, полученные на низших уровнях или экспериментально, а результатами f — внешние характеристики, связывает между собой средний и высший уровни проектирования. Этот уровень анализа, рассмотренный в гл. 4, отличается высокой трудоемкостью. На высшем уровне проектирования операции анализа заключаются в моделировании работы оптической системы в общей цепи преобразователей сигнала, входящих в оптический прибор. Входными данными для анализа здесь являются внешние характеристики оптической системы и других преобразователей, а также параметры входного сигнала (предмета). Результаты анализа представляют собой параметры выходного сигнала (изображения) и характеристики, описывающие качество функционирования всего прибора. На любом уровне различают одновариантный анализ, когда выходные характеристики f определяются для одного значения входных параметров х и многовариантный анализ, называемый также анализом чувствительности или влияния параметров, когда определяется зависимость выходных характеристик от небольших изменений входных параметров, т. е. находится матрица производных df/dx. Под синтезом (обратная задача) будем понимать первоначальное формирование конструкционной модели, т. е. определение значений параметров х, обеспечивающих заданные значения характеристик f (рис. 1.1). Синтез в большинстве случаев является эвристической и сугубо объектно-ориентированной операцией. Его содержание определяется конкретным типом синтезируемой системы. В настоящее время поддаются алгоритмизации только некоторые виды синтеза: поиск конструкции из существу- ющих вариантов при помощи информационно-поисковой системы (ИПС), синтез простейших типов оптических систем, набор систем из элементов с известными свойствами по методике М. М. Русинова [27], сборка оптической системы из нескольких узлов или компонентов, а также операции перестроения системы (оборачивание, изменение в масштабе, удаление и добавление элементов). В любом случае операция синтеза может быть разбита на два уровня: структурный синтез (наиболее эвристическая операция), в процессе которой определяются количество, типы и последовательность элементов, образующих систему, и параметрический синтез, задачей которого является получение конкретных значений конструктивных параметров элементов. Благодаря высокой степени эвристичности, в процессе синтеза редко удается получить систему полностью удовлетворяющую всем заданным требованиям, поэтому обязательной операцией является оптимизация, под которой будем понимать направленное изменение конструктивных параметров, начиная от некоторых исходных значений, с целью достижения наилучших значений характеристик. Математический аппарат оптимизации относится не к самому объекту — оптической системе, а к ее оптимизационной модели. Поэтому, когда эта модель построена, операция оптимизации является совершенно объектно-инвариантной и детерминированной. Выбор же оптимизационной модели, т. е. решение вопросов о том, что оптимизировать и чем оптимизировать, для конкретной оптической системы является весьма эвристической задачей. Способность правильного выбора приходит с опытом и при глубоком понимании принципов оптимизации. Синтезу и оптимизации посвящена гл. 5. Алгоритм проектирования на каком-либо иерархическом уровне, составленный из последовательности операций синтеза, анализа и оптимизации, изображен на схеме 1.1. В прямоугольниках показаны детерминированные операции, выполняемые ЭВМ, в трапециях — эвристические операции, выполняемые конструктором. Ромбами обозначены эвристические решения о дальнейшем ходе проектирования, принимаемые конструктором на основе оценки результатов операций, выполненных ЭВМ. Из схемы видно, что процесс проектирования является итерационным, т. е. содержит возвраты на начальные этапы с изменением и усложнением заданий на их выполнение. Заканчивается процесс после того, как результаты анализа на всех его уровнях будут положительно оценены конструктором. Заметим, что в процессе развития автоматизации проектирования все большее число ранее эвристических операций будет алгоритмизироваться. Весьма перспективными в этом направлении представляются самообучающиеся алгоритмы.
О
 ценка
качества изображения. Функция рассеяния
точки.
Тест-объект
"светящаяся точка".
Первичный
и наиболее универсальный тест -
объект при исследовании качества
изображения оптических систем -
тест-объект типа "светящаяся точка".
Он материализуется в виде круглой
диафрагмы малого диаметра, освещенной
проходящим светом (или ее уменьшенного
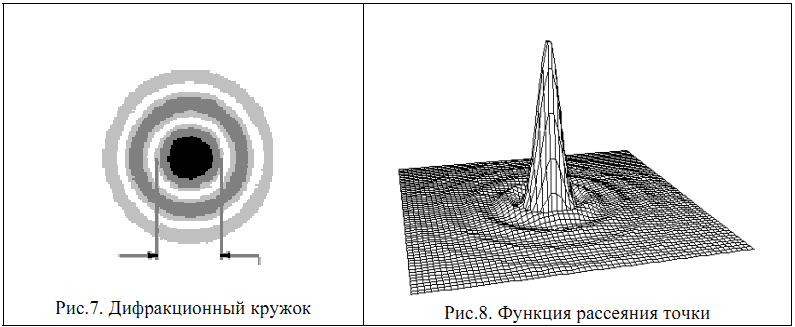
изображения). Изображение тест-объекта
"светящаяся точка" есть пятно
рассеяния или дифракционный кружок
(рис.7).
Наблюдение
дифракционного кружка, формируемого
исследуемой
системой,
позволяет
обнаруживать аберрации системы с
чувствительностью на
уровне до
0,1 λ. Функция, описывающая распределение
освещенности в изображении тест-объекта
"светящаяся точка", есть двумерная
функция, носящая название
функция
рассеяния точки
или ФРТ
(рис.8). Экспериментально найденная
ФРТ,
характеризуя качество системы,
позволяет учитывать все особенности
волновой
поверхности, сформированной системой,
в том числе и характер
микрорельефа
оптических поверхностей, дефекты
оптических материалов,
блики,
отклонение пропускания (или отражения)
на зрачке, сдвиги
изображения,
возникшие при работе прибора и т.д.
С помощью ФРТ в
осредненной
и мгновенной форме можно учитывать
флюктуации оптических
характеристик
воздушного тракта, непрерывно
изменяющиеся во времени по
сложному
случайному закону. ФРТ позволяет
надежно аттестовать качество
изображения
системы с несколькими зрачками. ФРТ,
являясь первичной
характеристикой
качества изображения, позволяет перейти
к другим требуемым
характеристикам
качества изображения, таким как ФРЛ,
ЧКХ, краевая функция,
концентрация
энергии и другие.
Тест-объект
"светящаяся точка" моделирует
важные для оптической измерительной
практики объекты, такие как, например,
небесные объекты типа звезд или
орбитальные объекты военного и невоенного
назначения.
ценка
качества изображения. Функция рассеяния
точки.
Тест-объект
"светящаяся точка".
Первичный
и наиболее универсальный тест -
объект при исследовании качества
изображения оптических систем -
тест-объект типа "светящаяся точка".
Он материализуется в виде круглой
диафрагмы малого диаметра, освещенной
проходящим светом (или ее уменьшенного
изображения). Изображение тест-объекта
"светящаяся точка" есть пятно
рассеяния или дифракционный кружок
(рис.7).
Наблюдение
дифракционного кружка, формируемого
исследуемой
системой,
позволяет
обнаруживать аберрации системы с
чувствительностью на
уровне до
0,1 λ. Функция, описывающая распределение
освещенности в изображении тест-объекта
"светящаяся точка", есть двумерная
функция, носящая название
функция
рассеяния точки
или ФРТ
(рис.8). Экспериментально найденная
ФРТ,
характеризуя качество системы,
позволяет учитывать все особенности
волновой
поверхности, сформированной системой,
в том числе и характер
микрорельефа
оптических поверхностей, дефекты
оптических материалов,
блики,
отклонение пропускания (или отражения)
на зрачке, сдвиги
изображения,
возникшие при работе прибора и т.д.
С помощью ФРТ в
осредненной
и мгновенной форме можно учитывать
флюктуации оптических
характеристик
воздушного тракта, непрерывно
изменяющиеся во времени по
сложному
случайному закону. ФРТ позволяет
надежно аттестовать качество
изображения
системы с несколькими зрачками. ФРТ,
являясь первичной
характеристикой
качества изображения, позволяет перейти
к другим требуемым
характеристикам
качества изображения, таким как ФРЛ,
ЧКХ, краевая функция,
концентрация
энергии и другие.
Тест-объект
"светящаяся точка" моделирует
важные для оптической измерительной
практики объекты, такие как, например,
небесные объекты типа звезд или
орбитальные объекты военного и невоенного
назначения.

Задание оптических сред.






Блочно-иерархический подход к проектированию ос.









З адание оптических поверхностей.





Методы автоматизированного проектирования ос.


К онструктивные параметры ос.





Синтез ОС. Процесс проектирования на любом иерархическом уровне можно представить в виде последовательности следующих типовых операций: анализа, синтеза и оптимизации. Под синтезом (обратная задача) будем понимать первоначальное формирование конструкционной модели, т. е. определение значений параметров х, обеспечивающих заданные значения характеристик f (рис. 1.1). Синтез в большинстве случаев является эвристической и сугубо объектно-ориентированной операцией. Его содержание определяется конкретным типом синтезируемой системы. В настоящее время поддаются алгоритмизации только некоторые виды синтеза: поиск конструкции из существующих вариантов при помощи информационно-поисковой системы (ИПС), синтез простейших типов оптических систем, набор систем из элементов с известными свойствами по методике М. М. Русинова [27], сборка оптической системы из нескольких узлов или компонентов, а также операции перестроения системы (оборачивание, изменение в масштабе, удаление и добавление элементов). В любом случае операция синтеза может быть разбита на два уровня: структурный синтез (наиболее эвристическая операция), в процессе которой определяются количество, типы и последовательность элементов, образующих систему, и параметрический синтез, задачей которого является получение конкретных значений конструктивных параметров элементов. Благодаря высокой степени эвристичности, в процессе синтеза редко удается получить систему полностью удовлетворяющую всем заданным требованиям, поэтому обязательной операцией является оптимизация, под которой будем понимать направленное изменение конструктивных параметров, начиная от некоторых исходных значений, с целью достижения наилучших значений характеристик. Математический аппарат оптимизации относится не к самому объекту — оптической системе, а к ее оптимизационной модели. Поэтому, когда эта модель построена, операция оптимизации является совершенно объектно-инвариантной и детерминированной. Выбор же оптимизационной модели, т. е. решение вопросов о том, что оптимизировать и чем оптимизировать, для конкретной оптической системы является весьма эвристической задачей. В прямоугольниках показаны детерминированные операции, выполняемые ЭВМ, в трапециях — эвристические операции, выполняемые конструктором. Ромбами обозначены эвристические решения о дальнейшем ходе проектирования, принимаемые конструктором на основе оценки результатов операций, выполненных ЭВМ. Из схемы видно, что процесс проектирования является итерационным, т. е. содержит возвраты на начальные этапы с изменением и усложнением заданий на их выполнение. Заканчивается процесс после того, как результаты анализа на всех его уровнях будут положительно оценены конструктором. Заметим, что в процессе развития автоматизации проектирования все большее число ранее эвристических операций будет алгоритмизироваться. Весьма перспективными в этом направлении представляются самообучающиеся алгоритмы.