19. Количественные закономерности питания организмов. Зависимость рациона от массы тела и концентрации корма в среде.

Рацион любого организма (R), или количество пищи, потребленное за единицу времени, в значительной степени определяется массой его тела (W). Примером этого являются данные для кубинского краба Menippe mercenaria. Этот важный промысловый вид является падальщиком, который питается, преимущественно, остатками погибших животных.

Если количество корма в среде находится с избытком, рацион крабов

возрастает с увеличением массы их тела. Однако увеличение рациона,

как и скорости дыхания животных, происходит в значительно

меньшей степени, чем массы тела.

Характер зависимости среднесуточного рациона (т.е. скорости питания) у животных от массы их тела аналогичен таковому для скорости дыхания. Однако можно отметить, что степенные коэффициенты в уравнениях для скорости питания в целом несколько ниже, чем для скорости дыхания.

У всех видов животных, особенно у водных беспозвоночных с фильтрационным питанием (например, у жаброногих и ветвистоусых раков), величина рациона в

значительной степени зависит от концентрации корма в среде. Как правило,

при низких концентрациях корма рацион особей возрастает пропорционально

их увеличению. Однако при дальнейшем повышении концентрации корма

увеличение рациона все более замедляется, а выше определенного предела он

стабилизируется на определенном уровне.

Однако многие виды с фильтрационным типом питания, например,

ветвистоусые раки, если концентрации корма (планктонные одноклеточные

водоросли) падает ниже определенного предела, вообще не способны его

улавливать. Обычно чем грубее их фильтрационный аппарат, тем при более

высоких концентрациях водорослей они теряют способность их потреблять.

Уравнение (4.5) для «грубых фильтраторов» может быть представлено в

следующей форме, называемой уравнением Ивлева – Винберга – Анисимова

R = Rmax[1 – e^{-λ(K – Kс)}].

20. Энергетический баланс и экологическая эффективность роста организмов. Поддерживающий рацион.

Экологич системы сущ-ют за счет постоянного потока и трансформации вещества и энергии. Основными элементами экологических систем являются организмы. Поэтому особенности трансформации вещества и энергии в экологических системах в значительной степени определяются закономерностями этих процессов на организменном уровне.

Баланс энергии у гетеротрофных организмов можно схематично представить следующим образом. Потребленная пища, или рацион частично усваивается организмом (усвоенная, или ассимилированная часть рациона), а частично выделяется наружу в виде непереваренных остатков (неусвоенная часть рациона). Усвоение пищи заключается в разложении ее сложных органических веществ (белков, углеводов, жиров) до сравнительно простых мономеров - аминокислот, моносахаридов и т.д. Одна их часть в процессе дыхания разлагается далее – до углекислого газа и воды с образованием АТФ.

Процессы обмена веществ, ведущие к высвобождению энергии пищи в организме, имеют общее название энергетический обмен.

Процессы образования в организме сложных органических веществ из более

простых называется пластическим обменом.

Согласно первому закону термодинамики, в любой системе между потреблением и расходом энергии существует равенство, т.е. соблюдается энергетический баланс. Для составления балансового равенства организма необходимо выразить каждый его компонент в единицах энергии. Баланс энергии организма можно представить в виде равенства:

R = P + T + N, (4.6)

где R – энергия потребленной пищи (рацион), Р – энергия пищи, использованная на увеличение массы тела особи (прирост), Т – энергия пищи, израсходованная в процессе дыхания, N – энергия пищи, которая потреблена организмом, но не усвоена им и выведена во внешнюю среду с фекалиями и другими продуктами распада.

Рацион организма, усвоенная часть которого равна его затратам энергии на дыхание, называется поддерживающим рационом (Rp). Очевидно,

Rp = T/U^-1. (4.8)

где U^-1 – усвояемость корма, или безразмерный коэффициент, представляющий

собой отношение к рациону его усвоенной части, т. е.

U^-1 = (P + T)/R = A/R.

21) Общие положения. Ростом популяции называется увеличение численности составляющих ее особей во времени в результате процессов размножения или иммиграции. При этом размеры, масса или возраст особей не имеют значения. Перед рассмотрением количественных закономерностей роста популяций необходимо выделить следующие основные понятия. Абсолютная скорость роста популяции (С), или прирост ее численности за (ΔN) за единицу времени ( Δt), т.е.: С = ΔN/Δt. Этот показатель имеет размерность «особи·время-1». Когда значения Δt достаточно малы, абсолютный прирост характеризует мгновенную скорость роста популяции, т. е. dN/dt, или первую производную численности по времени. Относительная скорость роста популяции (С’) определяется как прирост численности за единицу времени в расчете на одну особь:

C’ = (ΔN/Δt)–1/N. Значения С’ имеют размерность «время-1». Когда Δt значения

достаточно малы, получаем удельную скорость роста (r) популяции: r = (dN/dt) ·1/N.

Если dN/dt = 0, численность популяции остается постоянной. Тогда говорят, что популяция находится в стационарном состоянии. говорят, что популяция находится в стационарном состоянии. Соотношение между линейными размерами и массой животных. Увеличение линейных размеров или массы тела организма во времени

определяется соответственно как его линейный рост и весовой рост. Для животных соотношение между их линейными размерами (L) и массой тела (W)

выражается степенным уравнением: W = aLb, (5.1) где а и b – эмпирические коэффициенты; при этом, если L = 1, то а = W. Значения степенного коэффициента b для большинства беспозвоночных изменяются в пределах от 2,3 до 3,2 (Алимов, 1989).

При b = 3 рост организмов происходит с сохранением геометрического подобия пропорций их тела (изометрический рост). В этом случае с увеличением размеров тела организма в 2 раза, его масса возрастает в 8 раз. При b ≠ 3 геометрическое подобие пропорций тела в процессе роста нарушается (аллометрический рост). В двойных логарифмических координатах уравнение (5.1) трансформируется в уравнение прямолинейной регрессии: lg W = lga + b lgL. По (5.1) возможно определить массу особей по их линейным размерам. Для получения статистически достоверных значений коэффициентов а и b необходимо, чтобы масса тела исследованных организмов различалась не менеечем в 10 раз, а размеры их тела – в 2,5 – 3 раза.

Экспоненциальный рост численности популяции. Если значения удельных скоростей рождаемости (b) и смертности (d) в популяции остаются во времени постоянными, изменения ее численности будут передаваться экспоненциальным уравнением:

Nt = N_oe^bt – N_oe^-dt = N_oe^{(b – d) t}.

Логистический рост популяции. В природе, как правило, с ростом численности популяции скорость ее роста снижаться и в конечном итоге падает до нуля. Это приводит к стабилизации численности популяции на определенном уровне.

22) Экспоненциальный рост

Экспоненциальный рост численности популяции. Если значения удельных скоростей рождаемости (b) и смертности (d) в популяции остаются во времени постоянными, изменения ее численности будут передаваться экспоненциальным уравнением:

Поскольку b и d – постоянные величины, то и их разность b – d также является константой, соответствующей удельной скорости роста популяции (r). Тогда

где No – начальная численность особей, Nt – численность особей ко времени t. Значение r рассчитывается способом, аналогичным (7.3). Очевидно, при нулевой смертности удельная скорость роста численности популяции равна удельной скорости ее размножения. Рост численности популяции, соответствующий уравнению (8.1), называется экспоненциальным. В полулогарифмических координатах график уравнения представляет прямую линию, поскольку lnNt = lnNo + rt. (8.2)

В дифференциальной форме уравнение (8.1) имеет вид

dN/dt = rN. (8.3) Из (8.3) следует, что абсолютная скорость роста популяции возрастает прямо пропорционально ее достигнутой численности.Часто встречается утверждение, что экспоненциальный рост популяции имеет место только в оптимальных условиях среды и является очень быстрым. Это неверно, поскольку его единственным признаком является постоянство значений r, которое иногда может наблюдаться и в условиях, далеких от оптимальных.Даже стационарное состояние популяции может рассматриваться как ее экспоненциальный рост при r = 0. В природных условиях экспоненциальный рост встречается очень редко. Его примерами являются, как правило, молодые островные или пионерные популяции, которые попадают в условия избытка пространства и ресурсов, отсутствия хищников и конкурентов. Поэтому модель экспоненциального роста рассматривают в качестве оценки потенциальных возможностей роста популяции. В лабораторных условиях экспоненциальный рост может быть имитирован путем снятия факторов, лимитирующих скорость увеличения численности популяции. Например, в культурах микроорганизмов экспоненциальный рост поддерживается посредством постоянного удаления из среды прироста их биомассы и продуктов метаболизма и введения в нее свежих питательных веществ.На то, что увеличение численности организмов в природных условиях может происходить (но практически никогда не происходит) по экспоненциальному закону, впервые указал английский ученый Томас Мальтус в конце XVIII ст. Его труды имели огромное значение для формирования эволюционных представлений Чарлза Дарвина. В очень редких случаях наблюдается гиперэкспоненциальный рост, когда удельная скорость роста популяции возрастает во времени. Его примером является рост численности населения Земли в ХХ веке.

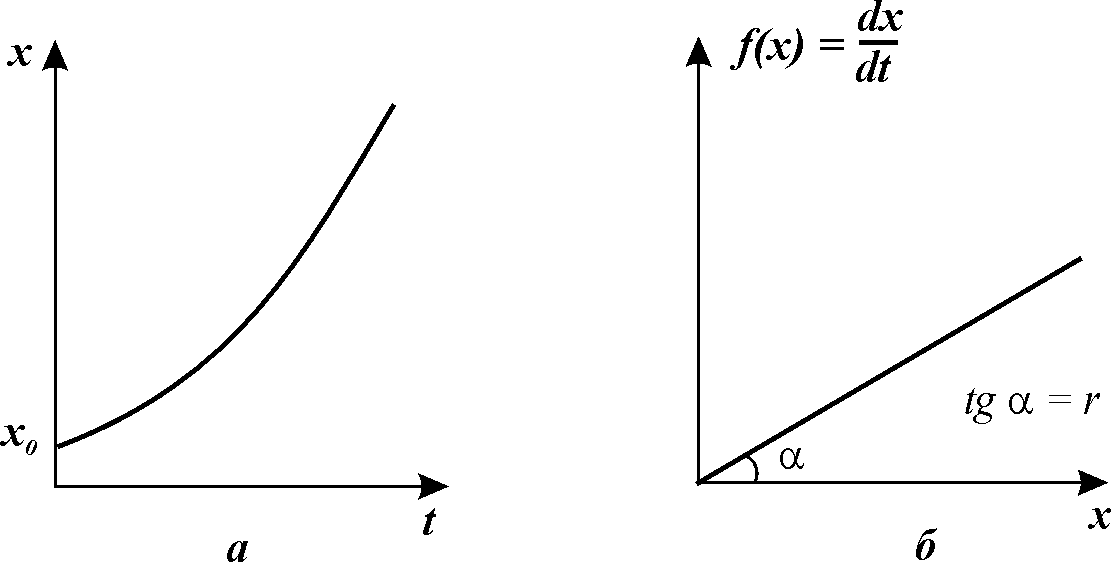
Рис. 3.2. Экспоненциальный рост. Зависимость скорости роста от численности (а) и численности от времени (б)

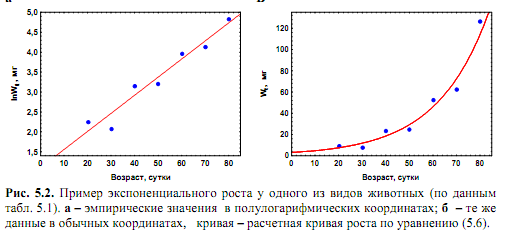
23) Параболический рост.

У абсолютного большинства животных значения Cw с увеличением массы их тела (W) снижаются. Отсюда их рост не является экспоненциальным и должен быть выражен другими способами. У многих видов ависимость Cw от W описывается степенным уравнением, (5.7) где N – эмпирическая константа, численно равная Cw у особи с массой тела, равной единице. В таком случае зависимость абсолютного прироста массы организма (dW/dt) от уже достигнутой его массы (W) следует уравнению:

. (5.8)

Интегральная форма уравнения (5.8) позволяет представить W как функцию времени:

. (5.9) где wo - масса новорожденной особи, to - условное время ее развития от w = 0 до wo, что соответствует длительности эмбриогенеза; Wt – масса особи к возрасту t, отсчитываемому от момента ее рождения. Если возраст отсчитывается от

начала эмбриогенеза, то вместо t + to следует брать t - to. У многих видов значение wo весьма незначительно по сравнению с массой взрослых особей, отсюда им вполне возможно пренебречь. В то же время, to может достигать до 10 % от предельного возраста особей, поэтому его нельзя приравнивать к нулю. С учетом этого, уравнение (5.9) можно упростить:

.

Если отсчет возраста особи (τ) вести от начальной точки роста, где t = 0 и w = 0, получаем

. (5.10) Если в (5.10) принять τ = 1, то выражение Nn1/n фактически является массой тела особи в возрасте, равном единице (W1). Тогда

. (5.11) График уравнения (5.11) спрямляется в двойных десятичных

логарифмических координатах:

Для перехода от (5.11) к (5.9) необходимо определить to, что легко сделать

из формулы

Тип роста животных, удовлетворяющий уравнениям (5.9 – 5.11), называется параболическим ростом. Он имеет место у многих видов насекомых на личиночной стадии развития, а также у большинства рыб. Однако если у насекомых при достижении имагинальной стадии рост прекращается, то рыбы растут непрерывно в течение всей жизни. При параболическом росте значения Сw снижаются с возрастом особей (τ)

по гиперболическому закону: Сw = 1/nτ.

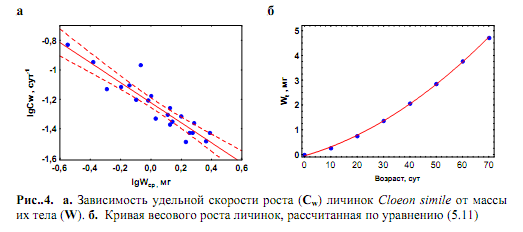
24) Асимптотический, или S-образный рост. В онтогенезе подавляющего большинства пойкилотермных животных самого разного таксономического положения удельная скорость роста с возрастом постепенно снижается до нуля. В таком случае при достижении определенного возраста или массы тела рост особи прекращается. При этом абсолютная скорость роста (dW/dt) в начальный период жизненного цикла растет, достигает своего максимума в возрасте, соответствующем точке перегиба на кривой роста, после чего снижается до нуля. У многих видов точка перегиба соответствует возрасту наступления половой зрелости.В таком случае левая часть кривой роста представляет собой восходящую вогнутую кривую, а правая – восходящую выгнутую кривую, асимптотически приближающуюся к характерному для каждого вида максимальному значению массы тела, называемому дефинитивной массой (Wd). Поскольку вся кривая роста особи имеет S-образную форму, подобный тип роста называется асимптотическим, или S-образным. Изменения dW/dt с увеличением массы тела особи (W) при S-образном типе роста во многих случаях удовлетворительно описываются эмпирическим уравнением (Bertalanffy, 1938): dW/dt = NWm - kW. (5.13)

где N, m и k – эмпирические коэффициенты.

Интегрирование уравнения (5.13) и некоторые дальнейшие преобразования

позволяют получить широко известное уравнение S-образного роста, которое

обычно называется уравнением Берталанфи:

Wt = Wd(1 – е-αt)1/(1-m) , (5.14)

где α - эмпирический коэффициент.

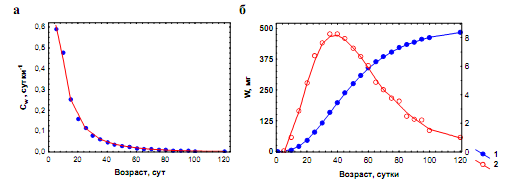
Рис. 5.5. Рост легочного моллюска Lymnaea hodutkae в геотермальном источнике

Ходутка (Камчатка) при 28–32 оС. а. Зависимость удельной скорости роста (Сw) от

возраста особей. б. 1 – кривая роста особей; 2 – зависимость абсолютного прироста

особей (dW/dt) от их возраста (по Хмелевой, Голубеву, Лаенко, 1985)

25) Связь скорости роста и скорости дыхания организмов. Г.Г.Винберг (1966) впервые показал, что тип и скорость весового роста организма тесно взаимосвязаны со скоростью его дыхания. Поскольку чистая экологическая эффективность роста организма (К2)

равна: то

Допустим, значения К2 на протяжении всей жизни организма остаются

постоянными, отсюда и выражение К2/(1–K2) = V также является константой.

Тогда: Р = V T. Поскольку прирост массы организма равен P = dW/dt, а зависимость его

трат на дыхание от массы тела выражается уравнением: то:

, (5.15) где N = V а. Разделив обе части уравнения (5.15) на W, получаем зависимость удельной скорости роста (Сw) организма от массы его тела:

. (5.16)

Поскольку коэффициент b < 1, значения b-1 всегда являются отрицательными. Легко видеть, что уравнение (5.16) аналогично приведенному ранее уравнению (5.7), характеризующему зависимость Сw от массы особи при параболическом типе роста.

Следовательно, если в процессе роста организма значение К2 у него остается постоянным, данный организм будет характеризоваться параболическим типом роста.

Интегрирование уравнения (5.15) позволяет получить уравнение параболического роста, тождественное (5.9): (5.17), где wо – масса новорожденных особей, wt – масса, достигаемая за время t + tо. Приняв wо = 0, из (5.17) получаем степенное уравнение (5.18) Легко видеть, что значение 1-b в уравнении (5.18) соответствует n в уравнении (5.9). Несмотря на снижение Сw, с массой особей, кривая параболического роста передается восходящей вогнутой кривой, никогда не выходящей на плато. Это обусловлено тем, что степенной коэффициент b в уравнении (3.1) зависимости скорости дыхания от массы организма меньше единицы, отсюда значения показателя степени 1/(1-b) в (5.17) всегда больше единицы. При b, близких к единице, следовательно, при высоких 1/(1-b), кривая параболического роста может визуально практически не отличаться от экспоненты, особенно в интервалах времени, соответствующих большим возрастам. Если b = 1, из (5.7) получаем Сw = N, т. е. независимость Сw от W, что соответствует уже не параболическому, а экспоненциальному типу роста. Таким образом, если интенсивность дыхания организма не снижается с увеличением массы его тела, рост организма имеет экспоненциальный характер. Экспоненциальный и параболический рост организмов предполагают

постоянство К2 на протяжении всего их жизненного цикла. Однако у абсолютного большинства видов значения К2 снижаются с возрастом или массой тела особей и в конечном итоге становятся равными нулю. Кривая роста при этом выходит на плато, что соответствует S-образному типу роста. В частном случае, когда снижается пропорционально достигнутой массы (w), или получаем:

, где , Wd – дефинитивная масса. В данном случае за K2max принимаются наивысшие значения К2, которые имеют место в начальный период роста у новорожденных особей. Интегрирование уравнения (5.19) и некоторые дальнейшие преобразования позволяют получить уже известное уравнение Берталанфи: , (5.20), где Легко видеть, что значение nk в уравнении (5.20) соответствует α в уравнении (5.14), a 1/n в (5.20) - 1/(1-m) в (5.14). Значение k можно также рассчитать, если известны значения Wd, а также

W1 и W2, соответствующие возрастам t1 и t2: Поскольку Г.Г. Винберг показал, что уравнение S-образного роста возможно получить из соотношения между скоростями роста и дыхания особи,1это уравнение в форме (5.19) часто называют уравнением Берталанфи Винберга. При этом если константы уравнения Берталанфи (5.14) являются чисто эмпирическими, то в уравнении (5.19) они имеют ясный биологический смысл

26) Основы балансовой теории роста. Баланс ассимилированной энергии организма можно представить в виде: А = Р + Т, где А – ассимилированная энергия рациона, Р – энергия прироста массы тела, Т – траты энергии на дыхание. Отсюда Р = А – Т. (5.21)

Поскольку , где R – рацион, U^-1 – усвояемость пищи, a рацион связан с массой тела степенной зависимостью R = pWk, получаем: А = U^-1pW^k.

Приняв усвояемость пищи (U-1) постоянной величиной и pU^-1 = m,

получаем степенную зависимость скорости ассимиляции пищи от массы тела: А = mW^k.

Поскольку зависимость трат на дыхание (Т) от массы особи также следует степенной функции Т = aW^b, уравнение (5.21) можно представить в виде: (5.22) Очевидно, прирост массы тела имеет место лишь когда mW^k > aW^b. При

mW^k = aW^b рост особи прекращается. Поскольку тогда mW^k/aW^b = 1 и в случае,

когда b ≠ k, легко рассчитать дефинитивную массу особи (Wd): (5.23)

В случае, когда b = k на двойном логарифмическом графике линии регрессии lgQ от lgW и lgR от lgW передаются параллельными линиями. В этом случае (конечно, если вторая линия проходит выше первой) рост организмов теоретически может продолжаться в течение всей их жизни, так что они никогда не достигнут дефинитивной массы.

Если все члены уравнения (5.22) разделить на W, получаем зависимость удельной скорости роста особи (Cw) от ее массы: (5.24)

Легко видеть, что постоянство СW в процессе роста достигается в единственном случае, когда b = k = 1: В таком случае рост особей будет экспоненциальным. Отсюда обязательным условием экспоненциального роста организмов является не только независимость интенсивности их обмена от массы тела, но и такая же независимость их скорости ассимиляции пищи. В случае, когда b = k < 1, получаем зависимость СW от массы тела, характерную для параболического роста:

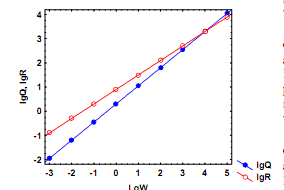
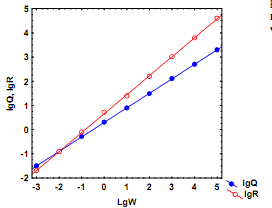
При b ≠ k линии регрессий lgQ и lgR от lgW пересекутся в диапазоне максимальных значений массы тела (рис. 5.6б). Удельная скорость роста в этом случае будет постепенно снижаться от максимальных значений в начале жизненного цикла до нуля у особей дефинитивной массы, которую можно рассчитать согласно (5.23). При b < k линии регрессии пересекутся в диапазоне минимальных значений массы тела (рис. 5.6в). В этом случае удельная скорость роста особи будет возрастать по мере увеличения ее массы сверх значения, рассчитанного согласно (5.23). Очевидно, подобный случай имеет биологический смысл

только у особей очень мелких размеров.

Рис. 5.6. Гипотетические случаи

соотношений между линиями

регрессии зависимости скоростей

дыхания (Q) и питания (R) от массы

тела (W) у животныха. Зависимость Q от W

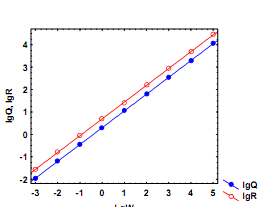
соответствует уравнению: Q = 2W0,75, а зависимость R от W – уравнению:

R = 5W0,75. В этом случае линии регрессии в логарифмических координатах идут параллельно, т.е. Wd = ∞

б. Зависимость Q от W соответствует уравнению: Q = 2W0,75, а зависимость R от W – уравнению: R = 8W0,60. В этом случае линии регрессии пересекаются при очень

высоких значениях массы особей, при Wd » 10 000

в. Зависимость Q от W соответствует уравнению: Q = 2W0,60, а зависимость R от W – уравнению: R = 5W0,80. В этом случае линии регрессии пересекаются при очень

низких значениях массы особей, приWd » 0,01

27) Важнейшим уровнем организации экологических систем является популяционный уровень. Как биологический термин это понятие впервые использовал германский зоолог Б. Иогансен в 1903 году.Популяцию в самом общем виде можно определить как совокупность особей одного вида, населяющих в течение неопределенно длительного периода времени (большого числа поколений) определенное пространство, внутри

которой осуществляется свободное скрещивание особей (панмиксия), и которая

достаточно изолирована тем или иным способом от других таких же популяций. Следует подчеркнуть, что поскольку популяция – это «совокупность особей одного вида», большой ошибкой является выражение «многовидовая

популяция». Популяция – это минимальная самовоспроизводящаяся группа особей.

Минимальный размер для самовоспроизводства популяции означает численность, достаточную для ее выживания при резких изменениях факторов среды на протяжении длительного числа поколений. Во многих популяциях наблюдаются «популяционные волны», или значительные многолетние изменения численности, диапазон которых в отдельных случаях достигают сотен и тысяч раз. Однако, несмотря на это численность популяции не падает ниже определенного критического уровня. Если это происходит, популяция исчезает. Каждая популяция является самостоятельной генетической системой. Она характеризуется определенным генотипическим своеобразием, которое

отличает ее от других популяций данного вида. Именно поэтому на популяционном уровне происходят процессы видообразования (микроэволюции) и приспособления (адаптации) к изменению факторов внешней среды. Приведенное выше общее определение относится преимущественно к популяциям двуполых видов, которые размножаются посредством полового размножения. Однако очень большому числу видов свойственны другие формы воспроизводства. У многих растений, протистов, беспозвоночных и низших хордовых наблюдается агамное, или бесполое размножение. Это вегетативное размножение у растений, почкование – у растений, губок, полипов, мшанок, деление тела надвое – у протистов или на несколько частей – у кольчатых

червей, оболочников и др. У некоторых групп беспозвоночных, таких как ракообразные (артемия, дафнии) и насекомых (тли), имеет место партеногенез, т. е. особая форма

полового размножения, когда яйцеклетка начинает делиться без оплодотворения.

Легочные моллюски, как гермафродиты способны размножаться самооплодотворением. Однако у большинства их водных видов оно является вынужденным способом полового размножения, так как имеет место лишь когда особь в течение длительного времени не может найти полового партнера. Напротив, у многих наземных видов легочных моллюсков этот способ размножения преобладает. Популяции тех видов, которые размножаются посредством партеногенеза, самооплодотворения, а также вегетативным способом часто называют агамыми популяциями. Агамная популяция – это совокупность клонов, или чистых линий, т. е. потомства от отдельных предковых организмов (особей-основателей), имеющих идентичные, если не считать мутаций, генотипы, занимающая

определенную территорию и достаточно изолированная тем или иным способом

от других таких же популяций. Агамные популяции одного вида часто характеризуются более значительными генотипическими и фенотипическими различиями, чем популяции видов с двуполым размножением. Это обусловлено тем, особи-основатели разных агамных популяций могли иметь резко различающиеся генотипы, которые сохранились и в их потомстве. Напротив, в популяциях двуполых видов генотип потомства представляет собой среднее между генотипами родительных форм, поэтому в процессе свободного скрещивания происходит нивелировка различий между генотипами отдельных особей.

Каждая популяция занимает собственное экологическое гиперпространство. Под ним можно понимать определенную территорию, на которой существует данная популяция (ареал), а также функциональную роль, которую она выполняет в биоценозе (экологическая ниша). Как правило, любой вид состоит из нескольких (иногда очень многих) популяций. Ареалы всех популяций одного вида образуют ареал вида, или определенную территорию, где постоянно обитают особи этого вида. Неправильно говорить «ареал распространения вида», поскольку ареал, в переводе и означает «область

распространения». Популяция – это система, элементами которой являются особи,

составляющие ее. Согласно принципу эмерждентности свойства популяции не являются простой суммой свойств составляющих ее особей. Совокупность взаимодействий между особями в популяции и между особями и внешней средой образует ряд принципиально новых свойств, характерных только для популяционного уровня организации биологических систем. В их числе – численность, плотность, биомасса, рождаемость, смертность и др. Взаимодействие особей в популяции также формирует ее структуру,

которую можно анализировать в разных аспектах. Обычно выделяют пространственную, половую, размерную и возрастную структуру популяции.

28) Численность популяций и методы ее определения. Численность популяции характеризует количество составляющих ее особей; она бывает абсолютной и относительной. Абсолютная численность может быть определена лишь в очень редких

случаях, когда четко очерчены границы популяции и есть возможность пересчитать всех особей в их пределах. Вполне возможно установить абсолютную численность популяций крупных древесных растений (например, секвойи), редких крупных млекопитающих (носороги, слоны и т. п.) и птиц (журавли и т. п.), обитающих на изолированных территориях, таких как заповедники и небольшие острова. Например, численность популяции европейского зубра Bison bonasus в Беловежской пуще известна с точностью до одной особи. Однако уже численность популяций мелких млекопитающих, например мышевидных грызунов, зайцев и даже диких кабанов и косулей, здесь определена лишь

приблизительно, поскольку она значительно изменяется по сезонам или годам.

Поэтому в экологии чаще всего анализируется не абсолютная, а относительная численность популяций, или их плотность. Плотностью популяции называется количество ее особей, приходящихся на единицу площади или объема пространства. Она выражается, например, в 5 экз·га-1; 10 экз· м-2; 50 экз·м-3. Зная площадь (или объем) ареала популяции и среднюю плотность особей в нем, можно получить определенное

представление и об ее общей численности. Достаточно точно плотность можно определить лишь для популяций неподвижных или малоподвижных видов, например растений или двустворчатых моллюсков. Поскольку чаще всего распределение особей в

популяциях неравномерное, обычно пробы численности берутся в разных точках ареала или в разных биотопах, а потом находят их средние значения. Определение плотности мелких или (и) мигрирующих видов животных представляет особые методические сложности. В таких случаях вместо абсолютных значений плотности часто используют ряд относительных показателей. Например, в энтомологии широко применяется оценка численности летающих насекомых в «ловушко-сутках», или в количестве насекомых,

попавших в стандартные ловушки за определенный период времени. В орнитологии в период размножения (когда птицы поют) применяется учет птиц по голосам на определенных маршрутах. Поскольку у большинства певчих птиц поют только самцы, выявленное количество птиц умножают на два. Определение численности популяций промысловых видов животных (киты, рыбы, ракообразные) имеет не только научное, но и большое практическое значение. В этих случаях широко используются следующие

понятия: промысловое усилие, или интенсивность промысла, – произведение количества орудий лова на продолжительность промысла; уловистость, или эффективность промысла, – отношение общего количества добытых особей к промысловому усилию. В китобойном промысле используется такой показатель, как «тонно-сутки», или общая масса китов, добытая в определенном районе океана за одни сутки период промысла.

Метод мечения. Всех добытых животных метят и отпускают обратно. Затем по доле меченых особей в их общем числе, добытых при втором облове, можно получить ориентировочные данные об абсолютной численности популяции.

Метод последовательных изъятий. Численность интенсивно эксплуатируемых популяций можно определить по снижению количества особей в последовательных изъятиях. При этом особи, изымаемые из популяции, обратно в нее не возвращаются.

Метод де Лури широко используется для приближенной оценки численности популяций промысловых китообразных.

Все рассмотренные выше методы определения численности популяций

основываются на следующих важных допущениях.

1. Численность популяции изменяется только в результате изъятия из нее

особей, а все другие факторы (эмиграции, иммиграция, рождаемость, смертность

и др.) не оказывают на нее во всем периоде изъятия существенного влияния.

2. Равная вероятность быть пойманными для всех особей.

3. Метки на животных должны быть легко распознаваемыми и не должны теряться.

Биомасса популяций. С численностью популяций тесно связана их биомасса, или общая масса особей на расчете на единицу площади или объема. В самом общем виде биомасса популяции (В) равна суммарной массе всех ее особей, обитающих на единице площади или объема:

где Wi – масса особей i-того размера. На практике биомассу чаще находят как произведение средней плотности популяции (N, экз м-2) на среднюю массу

одной особи в ней (W), т. е. B = W·N.

Биомасса популяций, как и масса отдельных особей, может быть выражена самыми разными способами. Чаще всего ее выражают в единицах массы – сырой, сухой, обеззоленной, массы органического углерода и т. д., например, 100 кг сырой массы·га-1 , 5 мг сухой массы·м-3 и т. п. Однако определение массы организмов при всей кажущейся простоте представляет серьезные методологические трудности. Практически у всех организмов имеются метаболически неактивные структуры, не принимающие значительного участия в процессах трансформации вещества и энергии. К ним относятся кора и одревесневшие ткани у растений, раковина у моллюсков, скелет у позвоночных и т. д. У травоядных млекопитающих приблизительно 20 % живой массы составляет находящийся в их желудках растительный корм. Учитывая неодинаковое содержание золы и сухого вещества у особей разных видов, в целях сравнения биомассу предпочтительнее выражать в энергетических единицах, например 5 ккал·м-2. С другой стороны, значительную часть массы древесных растений (и ее энергетического эквивалента) составляет мертвая древесина, обладающая высокой удельной энергоемкостью. Поскольку большинство метаболических процессов происходят в клетках, с методической точки зрения наилучшим показателем массы организма является суммарная масса его живой цитоплазмы. Некоторые соединения, например АТФ и пигменты фотосинтеза существуют только в живых клетках, вне их или в мертвых клетках они быстро разрушаются. Поскольку содержание этих соединений в клетках достаточно постоянно у разных видов, их масса может быть хорошим показателем общей массы цитоплазмы организмов. Однако количественное определение АТФ и пигментов фотосинтеза сопряжено со значительными методическими трудностями.

29) Размерная структура популяции выражает долю особей того или иного размера (или массы) в ее общей численности. В большинстве случаев размерную структуру популяций анализируют по линейным размерам особей, поскольку получить значения их массы не всегда возможно. Например, можно с высокой точностью и за короткое время измерить высоту большого числа деревьев, однако определить массу даже одного дерева весьма затруднительно. В практике лесоводства обычно измеряют не высоту деревьев, а диаметр их ствола на высоте приблизительно 1,5 м от поверхности почвы. Размерная структура популяций, как и их возрастная структура, может изображаться в табличной форме или наглядно в виде размерных диаграмм. Выбор числа размерных интервалов на таких диаграммах достаточно субъективен. Он зависит от размерного диапазона исследованных особей и количества промеренных экземпляров. Размеры особей в целом увеличиваются с их возрастом, поэтому в ряде случаев каждый размерный класс на возрастной диаграмме популяции соответствует определенному возрасту. Такие диаграммы называют размерно-

возрастными. Однако характер изменений размеров организмов с возрастом у разных видов существенно различается. Одни виды растут на протяжении всего жизненного цикла (растения, рыбы, двустворчатые моллюски и др.), хотя скорость их роста может снижаться с возрастом. У других видов (насекомые, птицы, отчасти млекопитающие и др.) рост резко прекращается после достижения половой зрелости. Поэтому в один размерный класс могут попадать особи разного возраста. Кроме того, у многих видов на размеры особей значительное влияние оказывают факторы среды, особенно обеспеченность пищей, плотность популяций и температура.

Типы временнóй динамики размерной структуры популяций. Размерная структура естественной популяции (как любой другой тип ее структуры) никогда не остается постоянной. Абсолютная и относительная численность размерных групп постоянно изменяется в результате появления в популяции новорожденных особей, перехода особей в результате их роста из одного размерного класса в другой, различной смертности особей из разных размерных классов, миграций особей из одной популяции в другую и т. д. На все эти процессы значительное воздействие оказывают как абиотические факторы – температура, фотопериод, так и биотические факторы – обеспеченность пищей, плотность популяции, межпопуляционные отношения. Вследствие этого размерная структура популяций постоянно претерпевает сезонные и многолетние изменения. Однако, несмотря на высокую степень лабильности размерной структуры, в ее изменениях можно найти ряд

общих закономерностей, на основе которых популяции всех видов живых

организмов подразделяются на четыре типа.

1. Популяции, состоящие из одновозрастных особей. К ним относятся популяции моноцикличных видов с непродолжительным (до года) жизненным циклом и коротким периодом размножения. Их примерами являются щитни и жаброногие ракообразные, обитающие во временных водоемах (весенних лужах, тундровых водоемах, рыбоводных прудах и т.п.), а также однолетние цветковые растения, особенно обитающие в арктических регионах. Эти виды значительную часть года проводят на стадии покоящихся яиц или семян. Выход личинок из покоящихся яиц и прорастание семян начинается, когда температура воды или почвы достигает необходимого уровня и длится очень непродолжительное время. Отрожденные особи быстро растут и вскоре достигают дефинитивных размеров, характерных для половозрелых особей. Повышенная скорость роста и развития у таких видов является адаптивным признаком, позволяющим им достичь половой зрелости и произвести потомство за короткий период существования временных водоемов (для водных беспозвоночных) или сезон вегетации (для растений).

Особи, достигшие половой зрелости, производят покоящиеся яйца или семена, после чего отмирают. Поскольку пополнение таких популяций молодью не происходит, их максимальная численность имеет место на начальных этапах существования. Затем в силу естественной смертности, выедания хищниками и иных причин она будет только снижаться и в конечном итоге станет равной нулю. Поэтому размерная структура таких популяций выражается одновершинной гистограммой с узким основанием. Ее модальный класс в течение вегетационного сезона постоянно смещается от меньших размеров в

сторону бóльших размеров, что обусловлено ростом особей. По смещению модального класса во времени можно реконструировать усредненную кривую роста особей данной популяции.

2. Популяции с дискретным распределением разных возрастных групп. Они характерны для животных и растений с длительным (не менее нескольких лет) жизненным циклом, размножающихся ежегодно в течение короткого промежутка времени. В их числе – большинство рыб, долгоживущие двустворчатые моллюски, речные раки, многолетние растения и т.п. В этих популяциях в любой момент времени присутствует ряд возрастных

групп: сеголетки (обозначение: 0+), годовики (1+), двухлетки (2+) и т.д. Поэтому они могут рассматриваться как совокупность некоторого числа когорт определенного года рождения. По средним значениям модальных классов в разных возрастных группах можно реконструировать усредненные кривые роста особей в популяциях за жизненный цикл.

3. Популяции с непрерывным размножением в течение сезона вегетации. Подобный тип популяций характерен для планктонных веслоногих и ветвистоусых раков, а также многих видов пресноводного зообентоса. В них присутствуют особи всех возрастов, но в результате непрерывного размножения выделение отдельных когорт невозможно. Поэтому численность особей, относящихся к каждой отдельной размерной группы, может не только уменьшаться в результате перехода особей на последующую стадию или их элиминации, но и возрастать по мере ее пополнения особями, переходящими из

младших возрастных стадий.

4. Популяции с незначительными различиями размеров тела особей. К этому типу относятся популяции одноклеточных организмов – бактерий и протистов, а из многоклеточных животных – коловраток. При оптимальных условиях жизненный цикл этих видов очень короткий – от нескольких часов до немногих суток, у одноклеточных организмов он соответствует промежутку времени между двумя делениями. Поскольку одноклеточные организмы размножаются делением надвое, различия по размерам тела особей в популяциях одноклеточных организмов незначительны. В популяциях коловраток самки производят крупную (по сравнению с ними) молодь, которая очень быстро (при 25 оС за 2–3 суток) достигает размеров половозрелых особей. По этим причинам размерный диапазон особей в популяциях одноклеточных организмов и коловраток очень узок и выделение в них отдельных размерных классов в абсолютном большинстве случаев (за исключением нескольких видов самых крупных коловраток) невозможно. В популяциях этого типа все особи фактически образуют единственную размерную группу, поэтому о сезонной или многолетней динамике их размерной структуры говорить не приходится.

30) Пространственная, или хорологическая структура популяции характеризует распределение особей в пределах популяционного ареала. Оно бывает равномерным и неравномерным – случайным или агрегированным. Равномерное распространение встречается достаточно редко, чаще всего в популяциях, созданных человеком, например, в посевах культурных растений и искусственных лесопосадках. В природных популяциях распределение, близкое к равномерному, чаще всего наблюдается у растений. Его примерами являются популяции полуводных растений – камыша, рогоза, вереска на пустошах, деревьев в густых лесах. Среди животных подобное распределение встречается почти исключительно у малоподвижных видов, в частности, у крупных двустворчатых моллюсков. Обычно равномерное распределение наблюдается, когда условия среды в ареале популяции достаточно однородны и не подвержены значительным колебаниям.

Рис. 3. Различные типы распределения особей в популяциях. Слева – равномерное, в

центре – случайное, справа – агрегированное

Гораздо чаще наблюдается хаотическое, или случайное распределение, когда в распределении особей в пределах ареала нельзя установить какой-либо четкой закономерности. Оно обычно характерно для подвижных видов животных, которые постоянно перемещаются в пределах ареала в поисках пищи или биотопов с более благоприятными условиями существования. Агрегированное, или пятнистое, распределение обычно встречается в популяциях растительноядных животных. Часто оно обусловлено пятнистостью в распределении потребляемых ими кормовых объектов. Для оценки характера распределения используют следующую методику. Весь ареал делят на

некоторое число равных по площади участков, а затем определяют численность

особей в каждом из них. Если участков слишком много, подсчеты производят в определенном числе случайно выбранных участков. По этим данным рассчитывают среднее число особей, приходящихся на один участок (cредняя плотность популяции, N) и дисперсию этого показателя (σ2). При равномерном распределении соотношение σ2/N близко к нулю, при случайном – близко к единице, а при агрегированном – больше единицы.

31. Поло-возрастная структура популяций.

Половая структура, или соотношение между самцами и самками в

двуполых популяциях, имеет важнейшее значение для их воспроизводства.

Различают первичное соотношение полов, определяемое в процессе

оплодотворения яйцеклетки, вторичное соотношение полов – у новорожденных

особей и третичное соотношение полов – при достижении половой зрелости.

У ряда видов креветок и рыб наблюдается протегиния. При рождении и

в начале репродуктивного периода особь является самкой, а к концу жизненного

цикла она превращается в самца. У некоторых креветок наблюдается и

противоположное явление – протерандрия.

У многих видов (например, у млекопитающих и птиц) первичное

соотношение полов близко к 1:1, что обусловлено генетически. У других видов

самки преобладают над самцами. Например, в популяции речных раков

соотношение между самцами и самками близко к 1:4.

Существует достаточно большое число видов, для которых характерно

чередование партеногенетического и двуполого размножения. Характерным их

примером являются артемии, ветвистоусые раки и коловратки. У этих видов

самцы появляются лишь в случаях ухудшения состояния условий среды.

Чередование способов размножения характерно также для тлей. Легочные

моллюски являются гермафродитами, которые могут размножаться как

перекрестным оплодотворением (норма), так и самооплодотворением.

Популяции многих двуполых растений, размножающихся вегетативным

способом, почти целиком представлены либо мужскими, либо женскими

экземплярами, в зависимости от пола экземпляра-основателя популяции.

Большое значение для оценки состояния популяций имеет доля

размножающихся самок в общей численности половозрелых самок. Если в сезон

размножения того или иного вида подобное этот показатель низок, можно

утверждать, что популяция находится под угрозой исчезновения, даже если ее

численность остается еще достаточно высокой.

Размножающиеся самки обычно идентифицируются по наличию у них

половых продуктов – яиц или икры. Например, самки многих видов

ракообразных вынашивают яйца на себе, у самок рыб заметны яичники, где

находится икра и т.д. Выметавшие икру самки двустворчатых моллюсков

определяются по характерным изменениям в строении гонад.

6.6. Возрастная структура популяций характеризует соотношение в

популяции различных возрастных групп. Группу одновременно отрожденных

особей в популяции называют когортой. На практике когортой считается

достаточно большая группа особей, отрожденных за короткий относительно

общей продолжительности жизни особей промежуток времени.

Критерии выделения когорт различны для разных видов. В популяциях

человека когортой считаются все индивидуумы с одним календарным годом

рождения. У большинства видов позвоночных (исключая мелких

млекопитающих), многих долгоживущих беспозвоночных и многолетних

растений размножение происходит один раз в году. При этом период

отрождения их молоди, выхода личинок из яиц или икры, прорастания семян и

т. п. приурочен к определенному сезону года и, как правило, непродолжителен.

Отсюда когортами в таких популяциях являются особи одного года рождения.

Если размножение происходит ежегодно, число когорт в их популяциях равно

максимальной продолжительности жизни особей.

В популяциях короткоживущих видов с постоянным размножением в

течение сезона вегетации когортами могут считаться особи, родившиеся в

течение одних суток, одной недели или месяца. Точное число когорт в таких

популяциях возможно определить лишь весьма приблизительно.

В отдельных случаях популяция может состоять всего из одной когорты в

течение всего периода ее существования, например, у однолетних растений,

или, у некоторых двухлетних видов с однократным размножением, в

определенные сезоны года.

Возрастную структуру популяции можно задать табличным или

графическим способом – в виде столбчатой диаграммы. Для видов с

максимальной длительностью жизни не более 10–20 лет, в качестве возрастного

интервала обычно используют 1 год. Пример подобной диаграммы для

популяции атлантической сельди приведен на рис. 6.4.

Для видов с большей длительностью жизни, например, древесных

растений, возрастные интервалы гораздо более продолжительны – от 20 до 200

лет и более (рис. 6.5).

Возрастную структуру популяций получить в тех случаях, когда возраст

входящих в нее особей может быть определен с достаточной точностью.

Например, в человеческой популяции эти данные можно получить по

паспортным данным населения.

В природных популяциях абсолютного большинства видов точный

возраст особей определить, как правило, очень трудно, а иногда вообще

невозможно. Определенное исключение составляют виды, у которых имеются

морфологические структуры, регистрирующие возраст, – годичные кольца, или

кольца роста, на горизонтальных спилах деревьев, раковинах двустворчатых

моллюсков, чешуе рыб и некоторые другие, которые позволяют определить их

возраст с достаточной точностью.

Однако точность подобных определений относительна, поскольку

«годичные кольца» в действительности образуются при любой остановке роста.

Например, если в каком-либо году за ранней и теплой весной последовали

поздние и холодные заморозки, то у деревьев или на раковинах моллюсков за

год могут образоваться не одно, а два кольца роста. Поэтому определение

возраста по годовым кольцам часто дает завышенные результаты. При

определенном навыке возраст жвачных млекопитающих можно определить с

достаточной точностью по степени истертости зубов. Возраст животных можно

определить посредством мечения особей и т. п.

По этим причинам в популяциях обычно выделяют только три

возрастные группы – предрепродуктивную, репродуктивную и

пострепродуктивную. Доля этих возрастов к общей продолжительности жизни

у разных видов сильно варьирует. У современного человека, например, на

каждый из этих возрастов в среднем приходится примерно треть жизни.

Напротив, у первобытного человека пострепродуктивный период был намного

короче.

У ряда видов, например насекомых и лососевых рыб, репродуктивный

период очень короткий, а пострепродуктивный отсутствует совсем. Так, самки

лососевых рыб (кета, горбуша), идущих на нерест из моря в реки, гибнут сразу

после вымета икры, а самцы – после ее оплодотворения. Некоторые цикады

достигают половой зрелости в возрасте 17 лет, при этом взрослые особи живут.