3. Появление многокритериальности

При широком применении методов исследования операций аналитики стали сталкиваться с задачами, где имеется не один, а несколько критериев оценки качества решения.

Рассмотрим описанную выше обобщенную транспортную задачу. Добавим к критерию минимальных расходов на обслуживание самолетов вполне естественные критерии максимума прибыли и максимума комфорта для пассажиров. Если есть три критерия, то необходимо согласовать их. Какое соотношение между оценками по критериям является наилучшим? Ответ на этот вопрос не определен условиями задачи. Нужна до­полнительная информация, которая может быть получена только от руководства авиакомпании.

Обратимся теперь к задаче о назначениях. Возьмем часто встречающийся случай, когда работы неодинаковы по своей важности, а исполнители различаются по качеству выполняемой работы [3]. Тогда к приведенному выше критерию минимальной стоимости можно добавить критерий качественного выполнения наиболее важных работ. Если есть уже два критерия, по которым следует оценивать качество распределения исполнителей по работам, то необходимо как-то согласовать их. Какое отклонение от минимума стоимости оправдывает высококачественное выполнение важных работ? Ответ на этот вопрос не вытекает из сформированной модели. Этот ответ вообще не может быть получен объективным образом. Информация о компромиссе может быть дана людьми, принимающими решения, на основе их опыта и интуиции.

Эти и многие им подобные задачи имеют следующую характерную особенность: модель, описывающая множество допустимых решений, объективна, но качество решения оценивается по многим критериям. Для выбора наилучшего варианта решения необходим компромисс между оценками по различным критериям. В условиях задачи отсутствует информация, позволяющая найти такой компромисс. Следовательно, он не может быть определен на основе объективных расчетов.

Анализ многих реальных практических проблем, с кото­рыми сталкивались специалисты по исследованию операций, естественным образом привел к появлению класса многокритериальных задач.

При появлении многих критериев задачи выбора наилучшего решения приобретают следующие особенности.

• Задача имеет уникальный, новый характер — нет статистических данных, позволяющих обосновать соотношения между различными критериями.

• На момент принятия решения принципиально отсутствует информация, позволяющая объективно оценить возможные последствия выбора того или иного варианта решения. Но поскольку решение так или иначе должно быть принято, то недостаток информации необходимо восполнить. Это может быть сделано лишь людьми на основе их опыта и интуиции.

4. Первые многокритериальные решения: сколько строить ракет?

Одним из первых подходов к принятию решений при двух критериях является метод «стоимость  эффективность». Он был разработан в конце 50-х годов в США для решения военных задач. В годы ракетно-ядерной гонки США  СССР одной из основных была задача о достаточности системы нападения для преодоления защиты потенциального противника. Метод «стоимость  эффективность» состоит из трех основных этапов:

1) построения модели эффективности;

2) построения модели стоимости;

3) синтеза оценок стоимости и эффективности.

Пример типичной модели, используемой в методе «стоимость  эффективность» для анализа вариантов построения военно-технических систем, дан на рис 3.1.

Модель состоит из двух частей  модели стоимости и модели эффективности. Эти модели используются для выбора военной системы с определенным числом ракет. Модель стоимости представляет зависимость общей стоимости от количества ракет, а модель эффективности — зависимость вероятности поражения целей от количества ракет. Обе модели в данном случае можно рассматривать как объективные: они строятся на базе фактических данных, надежного статистического материала. Однако выходные параметры этих моделей не объединяются посредством заданной зависимости; используется суждение руководителя, который определяет предельные значения стоимости, необходимые значения эффективности. Часто используют отношение стоимости к эффективности, но при этом рекомендуется обращать внимание на абсолютные значения этих величин.

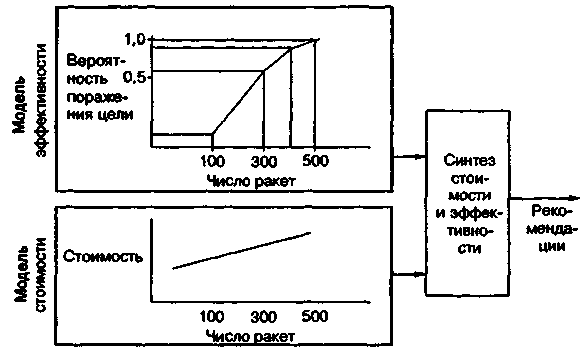
Рис. 3.1. Модели, используемые в методе «стоимость  эффективность»

Основное отличие приведенной модели от типичных моделей исследования операций заключается в появлении субъективных суждений при синтезе стоимости и эффективности. В общем случае на этапе синтеза стоимости и эффективности рекомендуется использовать два основных подхода: 1) фиксированной эффективности при минимально возможной стоимости (при таком подходе выбирается «самая дешевая» альтернатива, обладающая заданной эффективностью); 2) фиксированной стоимости и максимально возможной эффективности (случай бюджетных ограничений) [4]. Смысл этих подходов ясен  перевод одного из критериев оценки альтернатив в ограничение.

Но, при этом, сразу же, возникает вопрос: как, на каком уровне установить ограничение на один из критериев. Объективный и единственно возможный ответ на этот вопрос в общем случае не вытекает из условий задачи. Ни требуемая эффективность, ни бюджетные ограничения не устанавливаются обычно достаточно жестко. Очевидно, что при нескольких критериях этот же вопрос становится существенно сложнее. Иначе говоря, когда аналитик сам переводит все критерии, кроме оного, в ограничения, он совершает произвол, ничем не оправданный, с точки зрения руководителя, ответственного за решение проблемы.

В ряде случаев используют отношение двух указанных выше критериев. Авторы метода предостерегают против механического использования отношения стоимости к эффективности, указывая, что оно может быть одним и тем же при разных абсолютных значениях числителя и знаменателя.

Третий подход к синтезу стоимости и эффективности приводит к построению множества ЭджвортаПарето (рис. 3.2). Сравним два варианта на множестве ЭджвортаПарето. Вариант А менее дорогой, чем вариант В, но и менее эффективный. Вариант В более эффективный, чем вариант А, но и более дорогой. Сравнивая варианты, находящиеся на множестве ЭджвортаПарето, ЛПР останавливается на одном из них и делает свой окончательный выбор.

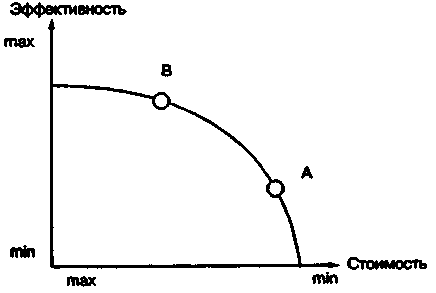
Рис. 3.2. Множество ЭджвортаПарето при двух критериях