9. Теорема Лиувилля.
Пусть функция u(x)
гармонична во всём пространстве Rn
и ограничена (
),
тогда
.
Д-во:
Возьмём 2 произвольные точки
.
Докажем, что
.
Для этого рассмотрим 2 шара
.
По 2 теореме о среднем получим:
,
Будем увеличивать R, пока эти 2 шара не пересекутся
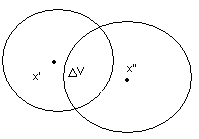
Замена
.
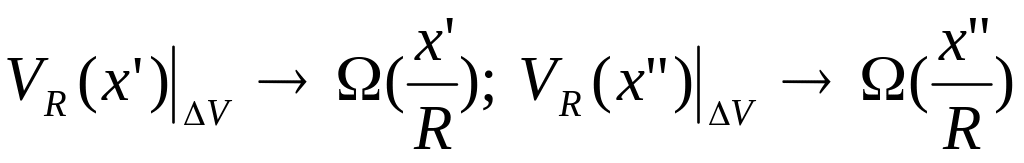
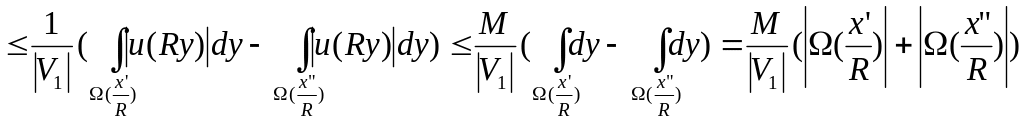
При
центры
стремятся к началу координат и шары
сливаются.
от R не зависит, но стремится
к 0 при
,
т.о.
.
В силу произвольности точек
функция
постоянна.
Теорема доказана.
№64. Преобразование Кельвина и его свойства.
В
курсе ТФКП вводилось понятие симметрии
точек относительно окружности единичного
радиуса. z
и z* - симметричны, если
они лежат на одном луче, выходящем из
(0,0), и |z|∙|z*|=1.
В случае Rn можно ввести симметрию точек относительно един. сферы Σ1
Пусть V – внутренность сферы без начала координат, V* - внешность.
Опр1 Точки х и х*, х,х*є Rn\{0} наз-ся симметричными относит единичной сферы, если они лежат на одном луче, выходящем из начала координат и ||x||∙||x*||=1 Заметим, что х*=x/||x||2 (1)
Опр 2 Преобразование К(х): Rn\{0}→ Rn\{0}, ставящее в соответствие каждой т х симметр ей точку относит единичной сферы, наз-ся преобразованием Кельвина пр-ва Rn Заметим, что К(х)= х*=x/||x||2 (2) В последнем рав-ве, устремляя х к 0 или ∞: К(0)= ∞, К(∞)=0
Св-ва преобразования Кельвина
Если х* - точка, симметр т х относит единичн сферы, то т х – точка, симметр т х* относит единич сферы. Др словами, K2=I
Преобр Кельвина: К(х):V→V*; K(x):V*→V; K(x): Σ1→Σ1
Будем рассм преобр-ие Кельвина как приложение.
Теорема Кельвина: Пусть Ωс Rn – область, возможно содержащая {0}, Ω*=К(Ω) (Преобр Кельвина обл Ω). Пусть ф-я U(x): Ω →R опр-на на Ω, кроме, быть может, начала к-т. Тогда ф-я V(y)=(1/|y|n-2)U(y*)=(1/|y|n-2)U(y/|y|2) (3) будет опр-на и гармонична в обл-ти Ω, кроме, быть может, т у=0. Наоборот, если ф-я V(y) опр-на и гармонична в обл Ω*, то ф-я U(x), опр-ая рав-м U(x)= (1/|x|n-2)V(x*)=(1/|x|n-2)V(x/|x|2) (3’) опр-на и гармон в обл Ω, кроме, быть может, нач к-т.
Док-во: Чисто выч-я
Опр Ф-ии U и V, опр-е рав-ми (3) и (3’), наз-ся преобразованиями Кельвина др друга.
№65. Скорость убывания на ∞ гармонич ф-й
Пусть ф-я U(x) гармонична в в окр-ти бесконечно удаленной точки и пусть U(x)=О(1), x → ∞ (n≥3), т.е. U(x) →→ 0, x → ∞. Тогда справедливы оценки: |U(x)|≤C/|x|n-2 , x→∞ (4). |Dα U(x)| ≤ C/|x|n-2+|α| , x→∞ (5). Если гармон ф-я хоть как-то убыв на ∞, то она убыв не медленнее фунд реш оп-ра Лапласа.
Док-во: При док-ве потребуется Теорема о миним особен гармонич ф-ии: Пусть U(x) – гармонич ф-я в некотор обл Ω, кроме начала к-т. Если U(x)=0 (Е(х)), х→0, где Е(х) – фунд реш оп-ра Лапласа, то ф-ю U(x) можно так опр-ть в нач к-т, что она будет гармонична в обл Ω (без док-ва)
Рассм ф-ю V(y)=(1/|y|n-2)U(y/|y|2), явл преобраз Кельвина ф-ии U(x). V(x) гармонична по Т Кельвина в окрест начала к-т, кроме, быть может, самой т нуль. Устремим у к 0, тогда y/|y|2 → ∞, у →0 и U(y/|y|2) → О(1), у →0. Тогда V(y)= (1/|y|n-2)O(1)=O(1/|y|n-2), y →0. В силу Т о миним особенности, у=0 явл правильной точкой, т.е. можно доопр-ть ф-ю V в т у=0, и V(y) ≤C при у →0 (т.к. V(y) – гармон во всей обл). U(x)=(1/|x|n-2)V(x/|x|2). При x→∞: |U(x)|≤C/|x|n-2 (4). Для получения (5) нужно продиф-ть (4) нужн число раз. Сл-е Д.
№66. Теорема о единств внешней задачи Неймана
Пусть ΩсRn – неогранич область, Г=∂Ω. Рассм в обл Ω внешнюю задачу Неймана для Ур-я Пуассона.
Решение задачи (1)-(3), если оно сущ-т, единственно.
Док-во: Без огр-я общности будем считать, что Ω – внешность нек-го ограниченного мн-ва G1. ПП: Рассм в области Ω ф-ии, явл решениями з-чи (1)-(3) в обл Ω U1 (x) и U2 (x). ω(x)=U1(x)-U2(x). Ф-я ω удвл задаче:
Заключим мн-во G1 в сферу достаточно большого радиуса R. Обозначим обл пересечения ΣR и Ω мн-м ΩR. Тогда ΩR – двусвязная область, причем ∂ΩR=ГUΣR Рассм выр-ние 0=ΩR∫ωΔωdx. (Δω=0) Распишем интегр по 1-ой ф-ле Грина:
Оценим
F(R) - невозраст ф-я по R,
g(R)=O(1)
ω=const, а это значит, из
(3’): ω=0, что и треб док-ть. Т.Д.
№67. Функция Грина. Функция Грина внутренней и внешней задач Дирихле для внутренности и внешности единичного шара.
Носитель обобщенной ф-ии.
Из определения обобщенной функции видно, что не имеет смысла говорить о ее значении в конткретной точке, но можно говорить об обращении ф-ии в нуль на некотором множестве. По определению: TєD(Ω) обращается в нуль на GєΩ, если (T,φ)=0, для любого φєD(Ω). Если рассмотреть объединение всех G, где T обращается в ноль:G=UαGα , то тогда носителем обобщенной ф-ии является suppT=Ω\G–замкнутое мн-во.
suppδ(x)={0}
suppδ(x-x0)={x0}
x0
suppφ(x),
то (δ(x- x0),φ)=0
x0єsuppφ(x), то (δ(x- x0),φ(x))=φ(x0)
Функция Грина.
Пусть Ω
Rn(ограниченная
или нет область). Предположим, в Ω мы
рассм. задачу Дирихле или Неймана для
ур-ия Пуассона.
ΔE(x)=δ(x)
Свойства E(x):
радиальная: E(x-ξ)=E(ξ-x)
ΔxE(x-ξ)=ΔξE(x-ξ)=δ(x-ξ)
Мы доказали третью формулу Грина для открытого класса.
Пусть u(x)єC2(Ω), Ω-огранич. u(x)є
,
тогда:
.Если
бы мы знали всю информацию о u(x): значения
в Ω, значения на границе Ω и значения
производной на границе по
,
тогда по третьей ф-ле Грина мы могли бы
полностью восстановить u(x). Однако, нам
известно только Δu и u|∂Ω, но
неизвестно
.
В случае задачи Неймана, нам известны
только Δu и
,
но неизвестно u|∂Ω.
Сл-но, ни в одном из этих случаев мы не
можем восстановить u(x) полностью.
Рассмотрим гармоническую в Rn
h(x) и применим 2-ую формулу Грина:
(1). Сложим с 3-ей формулой Грина:
.
Удобно ввести в рассмотрение функцию:
G(x,ξ)=E(x-ξ)+h(x,ξ), тогда последнее равенство
можно записать в виде:
(2). Такое равенство справедливо для
любой гармонической в
.
Ф-ия G, определенная выше,
называется функцией Грина соответствующих
краевых задач.
Замечание 1. Когда говорят о фундаментальности решения, мы говорим о нем, как о специальном обобщенном решении некоторого конкретного уравнения с постоянными коэффициентами, рассматриваемого к тому же во всем пр-ве. Если же мы говорим о функции Грина, то мы можем говорить о ней лишь как о функции, связанной не только с самим уравнением, но иобластью, в которой оно рассматривается, и с характером краевых условий.
Замечание 2. Когда мы подбираем h, эта
функция должна быть гармонической по
ξ и зависеть от х как от параметра.
=
,
xєΩ;
.
Более того, из симметричности
фундаментального решения, мы можем
сделать вывод, что
=
,
x,ξєΩ
xRn : x<1}; ГxRn : x=1}-сфера
Рассмотрим в зад Дирихле для ур-ия Пуасона:
u(x)=f(x), x (1)
u||x|=1=(x) (2)
Теорема
Ф-ия Грина задачи (1), (2) при n>=1
G(x,)=E(x-)-
*-точка
симметричная точке
относит единичн сферы
Док-во
Перепишем определение ф-ии Грина для данной области.
Ф-ия G(x,) наз ф-ей Грина зад (1), (2) если выполняются условия:
G(x,)= G(, x) x,
x G(x,)= G(x,)=(x-)
G(x,)| ||=Г=0 x
Проверим симметричность
1 G(,x)=E(x-)-
=
,
|y-z|2=<y-z,y-z>=|y|2+|z|2-2<y,z>
||2|x|2+(
)2-2<||x,
>=|x|2||2+(
)2-2<|x|,
>
равенство выполнено
2 x
G(x-)=(x-)
-
supp
=0
3 G(x,)| ||=1.2= (E(x-)- )| ||=1 =0 {* при ||=1} эта ф-ия явл ф-ей Грина.
Теорема док-на.
Теорема В случае n=2 ф-ия Грина для задачи Дирихле имеет вид:
G(x,)=E(x-)-
№68. Функции Грина внутренней и внешней задачи Дирихле.
Пусть -ограниченная областьRn с кусочно-гладкой границей Г=; рассмотрим в внутреннюю задачу Дирихле для ур-ия Пуассона:
{ u(x)=f(x), x
{ u|г=(x)
Опр. Ф-ия G(x,)- набора (2n) переменных (x,) наз. ф-ей Грина внутренней задачи Дирихле для ур-ия Пуассона, если это регулярная обобщенная ф-ия такая, что
G(x,)= G(, x)
x G(x,)= G(x,)=(x-)
G(x,)|Г=0 x
тогда согласно равенству (2формула для u(x)) решение задачи Дирихле имеет вид:
u(x)=
Построение G(x,):
G(x,)=E(x-)+h(x,), E –известное фундаментальное решение.
Найдем h(x,)
h(x,)=0
h(x,)|Г = -E(x-)
Если -неогранич, тогда появляется условие регулярности на :
u(x)=f(x), x
u|г=(x)
u(x)= O(1), n=2, x - обеспечение единств решения внешн краевых задач
o(1), n x
тогда определение ф-ии Грина для внешней задачи остается тем же, то есть:
1 G(x,)= G(, x)
2 x G(x,)= G(x,)=(x-)
3
G(x,)|Г=0
x
4
G(x,)= O(1), n=2, x - обеспечение единств решения внешн краевых задач
o(1), n x
решение имеет такой же вид, что и для внутренней зад, а для h появл условие регулярности на
h(x,)=0
h(x,)|Г = -E(x-)
O(1), n=2, x - обеспечение единств решения внешн краевых
G(x,)= Задач
o(1), n x
схема решения задач
1 Поиск фундаментального решения оператора
2 Построение ф-ии Грина по определению
3 Решение вспомогательной задачи (ф-ия Коши)
№69. Симметрия ф-ии Грина
Требование к симметрии ф-ии Грина зад Дирихле явл лишним и его используют, чтобы упростить док-во.
Теорема (симметрия ф-ии Грина)
Если x, , тогда G(x,)= G(, x)
Док-во
Применим вторую формулу Грина в обл = \(V(x) V()), где настолько мало, чтобы V(x)
V()
u(y)= G(y,)
v(y)= G(y,x)
отметим, что в обл u(y) и v(y)- гармонические:
u(y)= v(y)=0 в
На границе : u(y)= v(y)=0
= V(x) V()= S(x) S()
Вторая формула Грина
Пользуясь представлением
u(y)=E(y-)+h(y,)
v(y)=E(y-x)+h(y,x)
и устремляя 0 точно также как и при док-ве фундаментального решения оператора Лапласа получаем, что u(x)=v()
Теорема доказана.
№70. Функция Грина внутренней задачи Неймана.
Рассмотрим внутреннюю задачу Неймана для уравнения Пуассона:
Необходимое условие разрешимости:
Если взять
,
то формула (2) дает решение:
Тогда
.
По свойствам гармонической функции
интеграла по сфере от гармонической
функции равен 1. Поэтому возьмем условие:
Т.к. решение задачи Неймана определяется с точностью до константы, этой константой можно пренебречь.
-
площадь поверхности границы. Тогда:
Определение: Функцию
будем называть функцией Грина внутренней
задачи Неймана, если
1)
2)
3)
Тогда решение будет иметь вид:
Тогда
,
где
(h- гармоническая, 2 св-во следует из условия (3) ф-и Грина)
№71.Функция Грина внешней задачи Неймана.
Рассмотрим в области
внешнюю задачу Неймана
.(При
n=2 для внешней задачи
Неймана существует необходимое и
достаточное условие и функция Грина
строится аналогично внутренней задачи
Неймана).
Необходимого условия разрешимости нет.
Определение: Обобщенная функция
двух наборов переменных x,
называется функцией Грина внешней
задачи Неймана, если
1)
2)
3)
4)
Тогда решение будет иметь вид:
, где
№72.Метод отражения. Функция Грина для полупространств.
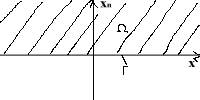
{Далее описание метода отражений см. в вопр. 73-74}
№ 73 Функция Грина внешней задачи Дирихле для полупространств.
Рассмотрим в области внешнюю задачу Дирихле:
Перепишем определение функции Грина внешней задачи Дирихле для этой области.
Опр. Обобщенная ф-я 2-х наборов
называется ф-й Грина внешней задачи
Дирихле, если:
1)
2)
3)
4)
Тогда решение:
- единичный пробный заряд положительного
знака. Потенциал в нем
.
Возьмем
- симметричную
относительно оси x’
и поместим в эту точку единичный пробный
заряд противоположного знака. Потенциал
-
.
Тогда потенциал, создаваемый обоими
зарядами – ф-я Грина.
Док-во:
1)
.
Возьмем
,
найдем x* ,
получим
2)
supp
;
supp
поэтому
эта точка нас не интересует.
3)
при
.
4) При
оба слагаемых стремятся к 0.
Доказано.
№ 74 Функция Грина внешней задачи Неймана для полупространств.
Опр. Обобщенная ф-я 2-х наборов
называется ф-й Грина внешней задачи
Неймана, если:
1)
2)
3)
4)
Тогда решение:
- единичный пробный заряд положительного
знака. Потенциал в нем
.
Возьмем
- симметричную
относительно оси x’
и поместим в эту точку единичный пробный
заряд такого же знака. Потенциал -
.
Тогда потенциал, создаваемый обоими
зарядами – ф-я Грина.
Док-во:
1)
.
Возьмем
,
найдем x* ,
получим
2)
supp
;
supp
поэтому
эта точка нас не интересует.
3)
4) При
оба слагаемых стремятся к 0.
Доказано.