№42. Уравнения специальных функций. Уравнение Бесселя.

Специальные функции одной переменной являются решениями обыкновенного дифф. уравнения:

Предположим, что - один раз непрерывно дифф-ма на , , , , (2), .

Здесь - непрерывная на функция.

Т.о. точка , в которой коэффициент при старшей производной уравнения (1) обращается в ноль, является особой точкой этого уравнения.

Из курса обыкновенных дифф. уравнений нам известна

Лемма.

Пусть и - два линейно независимых решения уравнения (1), коэффициент которого удовлетворяет условиям (2). Тогда если - ограниченное решение, имеющее конечный предел в точке , то второе решение при является неограниченным, причем если , то имеет в точке логарифмическую особенность, а если имеет в точке ноль того порядка(нютого), то функция имеет при полюс того порядка.

Уравнением Бесселя (уравнением цилиндрической функции) называют

, , .

Свойства Гамма-функции.

, - комплексная переменная, .

1. 

2. 

3. Теорема умножения:

4. (3).

П

редставление гамма-функции в виде контурного интеграла Римана-Ханкеля. любой контур на комплексной плоскости , обходящий точку против часовой стрелки, и концы которого уходят на бесконечность вдоль положительной вещественной оси.

Заметим, что интеграл (3) определяет функцию всюду на комплексной плоскости .

При гамма-функция имеет полюсы.

5. 

=

,

=

(4)

№43. Степенной ряд для функции Бесселя.

Будем далее считать, что всегда

Из уравнения Бесселя следует, что данное уравнение имеет особую точку , поэтому его решение можно искать в виде степенного ряда (метод Фрабениуса).

(5)

Подставляя (5) в уравнение Бесселя и приравнивая коэффициенты при равных степенях:

(6)

если (7)

Из остальных уравнений:

если , то (8)

Из второго уравнения (6) следует, что (9)

(10)

Получаем, что все нечетные коэффициенты равны нулю.

Вернемся к равенству (7) и рассмотрим 2 случая.

Первый случай .

Возьмем в (10) , и получим (11)

(12)

Учитывая, что решение однородного уравнения Бесселя определяется с точностью до произвольного множителя , выберем его в виде:

(13)

Тогда из формулы (12) и (13) получаем: (14)

Рассмотрим следующий ряд:

(15)

Ряд (15) называется функцией Бесселя (функцией Бесселя первого рода).

С помощью признака Даламбера легко установить, что ряд сходится абсолютно при .

Функция (15) называется частным решением уравнения Бесселя.

Функция Бесселя, определяемая для вещественного аргумента рядом (15), может быть аналитически продолжена с положительной вещественной полуоси на комплексную плоскость с разрезом по отрицательной части вещественной оси.

При нецелом точка является точкой ветвления функции .

Полученная функция Бесселя комплексного аргумента является аналитической в области .

При - целом функция Бесселя оказывается аналитической на всей комплексной плоскости ,т.е. целой функцией комплексной переменной .

Второй случай .

Полагаем в (10) , и проделав выкладки с учетом того, что формула (8) дает нам, что , т.е. , аналогичные первому случаю, получаем определение:

(16) .

Ряд (15) при наз-ся функцией Бесселя порядка , определяется формулой (16).

При нецелом функция (16) представляет собой второе решение уравнения Бесселя, линейно независимое от (15).

Из (15) и (16) вытекает, что в случае нецелого эти функции по-разному ведут себя в нуле: функция имеет в нуле ноль того порядка, а, следовательно, вторая функция имеет в нуле полюс того порядка.

Таким образом при функции (15) и (16) линейно независимы и образуют фундаментальную систему решений уравнения Бесселя порядка .

При целых значениях индекса определение функции (16) лишено смысла, т.к. гамма-функция в знаменателе при отрицательных целочисленных значениях обращается в бесконечность.

Продолжим (16) по непрерывности по индексу на целые значения .

Так как , то суммирование в формуле (16) фактически начинается со значения , поэтому

.

При функции линейно зависимы и не образуют ФСР. Следовательно, при верно .

Для того чтобы найти общее решение уравнения Бесселя, необходимо построить второе линейно независимое от функции частное решение уравнения Бесселя.

Введем функцию: (17)

(17) – функция Бесселя второго рода того порядка.

Это решение уравнения Бесселя и в том случае, когда целое число, причем функции и линейно независимы при .

И, следовательно, при они образуют ФСР.

Общее решение уравнения Бесселя можно записать в виде:

(18)

№44. Рекурентные формулы.

(19) (20)

Докажем формулу (19):

При это константа

Тем самым формула (19) доказана. Ч.т.д.

Формула (20) доказывается аналогично.

Если , то из (19) получаем равенство: .

В формулах (19) и (20) мы произведем дифференцирование.

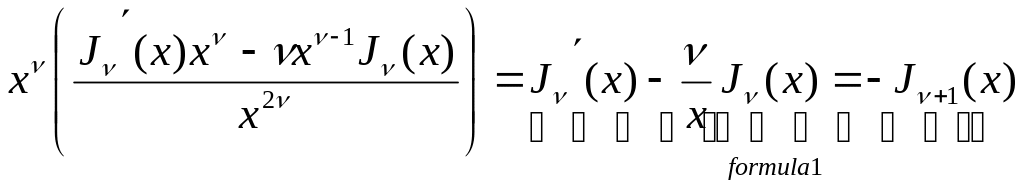
Продифференцируем формулу (20)

,

Сложим эти формулы(formula1 + formula2):

Теперь вычтем эти формулы:

Получаем:

(21)

Это рекурентная формула для функции Бесселя.

Функция Бесселя полуцелого порядка.

С помощью формулы (15) найдем и :

Подставим все это в нашу формулу:

Аналогично доказывается функция Бесселя порядка :

Эти ф-ии образуют два линейно независимых решения уравнения Бесселя порядка .

Замечание 1

Заметим, что из (21) и полученных представлений мы можем получить представление функции бесселя порядка , где

здесь и - полиномы степени не выше относительно , причем .

Замечание 2

Отметим также, что Лиувилль доказал, что цилиндрические функции полуцелого порядка являются единственными цилиндрическими функциями, выражающимися через элементарные функции.

№45

Из формулы (4) если z=k+𝛎 то формула принимает вид: . Подставим в формулу (15). (e^iπk=cosπk=(-1)^2k) (22). Пользуясь теоремой Коши выберем в качестве 𝛄 контур (рисунок), состоящий из луча на верхнем берегу разреза вдоль положительной части вещественной оси окружности с центром t=0 и радиусом x/2, который обходиться против часовой стрелки, и луча на нижнем берегу разреза. Сделаем замену , при этом наш контур (комфорное отображение) перейдёт в контур (рисунок)

, .

это интегральное представление Зоммерфельда для функции Бесселя. В частном случае в этой формуле сделаем замену ξ=ζ₂ при ζ=±π+i ζ₂, α= ζ₁, ζ= ζ_1.

, при ν=n замена α=φ+π/2. Тогда, т.к. подынтегральная функция является периодической и интегрирование можно производить по любому промежутку с L=2π, получим 2-ю интегральную формулу для функции Бесселя

, тогда для плоской волны (функция е имеет разложение в ряд Фурье) поскольку последнее представление является формулой для коэффициентов Фурье этого разложения.

№49. Метод Фурье решения краевых задач для ур-я Лапласа в круге.

Рассмотрим внутреннюю краевую задачу для ур-я Лапласа в круге:

(1)

, двумерный случай.

круг,

окружность.

Перейдем к полярным координатам:

(2)

Решим методом Фурье:

Подставим в ур-е Лапласа:

, т.к. независимы.

(3)

- нет периодичности

Из 2) и 3)

Вернемся к ур-ю 3:

ур-е Эйлера

В 1-е ур-е:

- выражение, дающее решение ур-я Лапласа в круге, удовлетворяющее условию периодичности.

Функция должна быть непрерывна в 0 огр-на

Найдем решение задачи (1):

Разложим в ряд Фурье

, где

№50 Задача Дирихле и Неймана в круге.

Из общего случая можно выписать частный случай:

, Это задача Дирихле в круге

; ;

замена

- Это задача Неймана

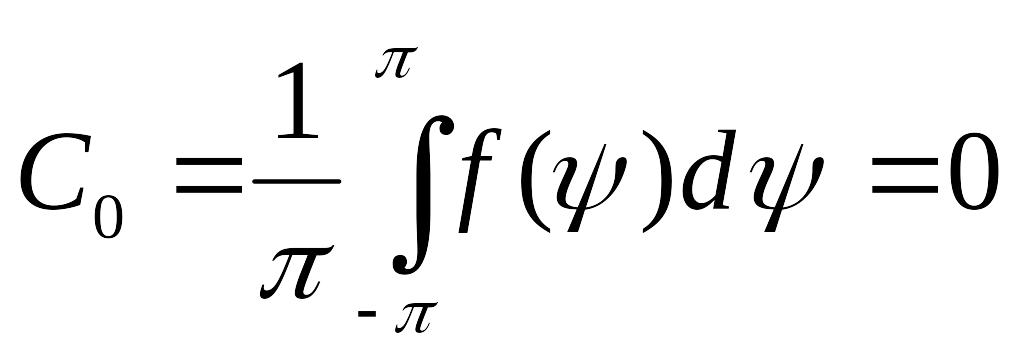(необходимое условие разрешимости внутренней задачи Неймана). Решение определяется с точностью до константы. Решение:

Замечание: Если в двух последних формулах положить , то они будут определять решение внешних задач Дирихле-Неймана.

№51 Интеграл Пуассона.

Получим иную формулу решения задачи Дирихле для круга.Преобразуем полученное решение :

Воспользуемся следующей формулой:

; ,

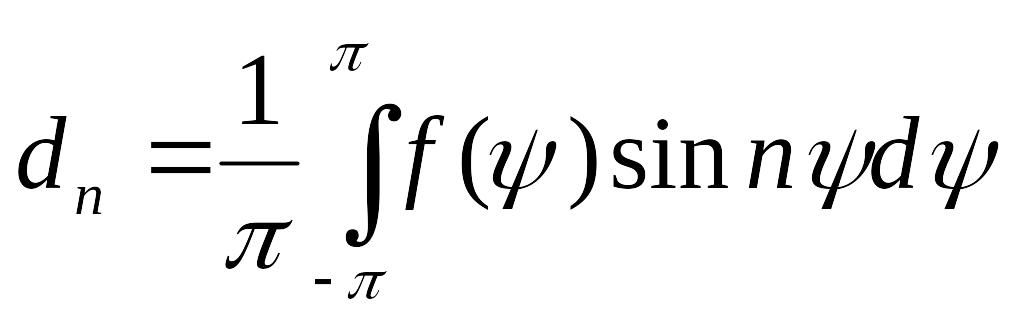
и подставим в выражение для :

(*) ,

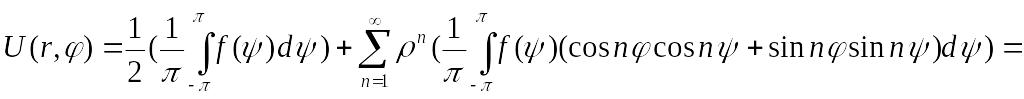
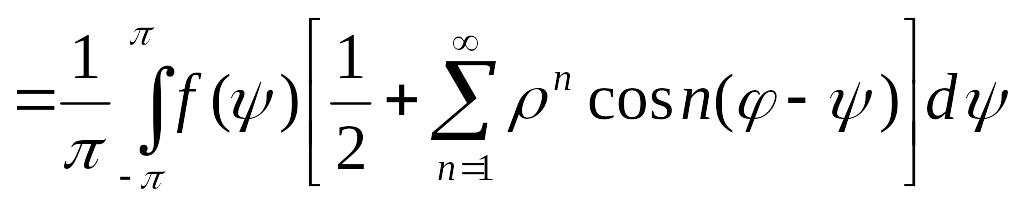Выражение в квадратных скобках запишется в виде:

где , -сопряженное, причем

Следовательно, последние суммы-суммы беск. убыв. геометрических прогрессий:

;

Заметим, что и

Подставляя в (*), получим:

-интеграл Пуассона для круга.

Еще одна формула решения. Интеграл в правой части называется интегаралом Пуассона.

№52 Обобщенные функции.

Цель теории обобщ-х функций – устранить недостаток невозможности дифференцирования. Пр-во обобщ-х ф-ций – наименьшее расширение пр-ва непрерывных ф-ций, в к-ром дифференцирование выполнимо.

Пример Попытаться определить плотность, создаваемую точкой массой 1, считая, что точка находится в (0,0). Чтобы определить эту плотность, распредел. равномерно эту массу в шаре радиуса 1 с центром в т. (0,0). В результате получим среднюю плотность:

В качестве искомой плотности попыт. найти поточечный предел послед-сти средних пл-стей:

От пл-сти естественно потребовать, чтобы . В силу рав-ва (1) интеграл слева всегда равен 0. Это противоречие показывает, что поточечный предел послед-сти пл-тей при не может быть принят в качестве пл-сти .

Определение Посл-сть линейных функционалов на G слабо сходится к линейному ф-лу на мн-ве G, если она сходится к f на каждом элементе , т.е. . Вычислим слабый предел посл-сти ф-ций при , т.е. для любой фиксированной непрерывной ф-ции найдем предел числовой посл-сти при . П-жем, что .

Т.к. непрерывна, то в точке 0:

Рассмотрим модуль разности (учитывая, что ):

Слабым пределом посл-сти ф-ций при явл-ся функционал, сопоставл. каждой непрерывной ф-ции от x ее значение в 0. Этот ф-л мы и принимаем в качестве плотности (Дельта-функция Дирака).

Т.о., ,где символ , . Пл-сть не может быть описана в рамках классической тории.

№53 Пространства основных и обобщенных функций

Рассмотрим классическую функцию , где - открытое множ-во.

Определение Носителем ф-ции f(x) – supp f(x) наз-ся множ-во вида: . Ф-ция имеет финитный носитель (финитна), если ее носитель есть компактное подмнож-во .

Символом обозначают множ-во всех бесконечно диф-х ф-ций, если эти ф-ции на множ-ве , то

Пример

Упражнение Показать, что - бесконечно диф-ма (точки -1,1). Запас таких ф-ций достаточно велик, т.е., зная можно построить: . Пр-во явл-ся линейным пр-вом.

Определение Будем говорить, что посл-сть ф-ций сходится к ф-ции , если:

1)

2) (равномерная сх-сть самой послед-сти ф-ций и всех производных)

Пр-во с введенной так сходимостью обозначим . Пр-во будем называть пр-вом пробных финитных ф-ций.

Рассмотрим пр-во пробных ф-ций и поставим в соответствие , т.е. зададим функционал

Определение Функционал, действ. наз-ся линейным, если вып-ся св-во:

Функционал наз-ся непрерывным, если

Совокупность всех линейных непрерывных ф-лов назовем пр-вом обобщенных ф-ций (или распределением, сопряженным к пр-ву ) и обозначим . Посл-сть обобщенных ф-ций сх-ся к обобщенной ф-ции , если: ( - пробная ф-ция). Рассмотрим множ-во

Определение Обобщенная ф-ция наз-ся регулярной, если она опред-ся нек-рой фиксированной, классической ф-цией . Если нельзя найти такую ф-цию f(x), то Т наз-ся синулярной.

Пример n=1 . Рассмотрим интеграл (возьмем такую f(x)). Построим посл-сть . П-жем, что выполнено . Рассм-м Т. о., мы построили посл-сть классических ф-ций , сход-ся к ф-ции Дирака .

По определению, - сдвиг дельта-ф-ции.

Пример Нужно пок-ть, что

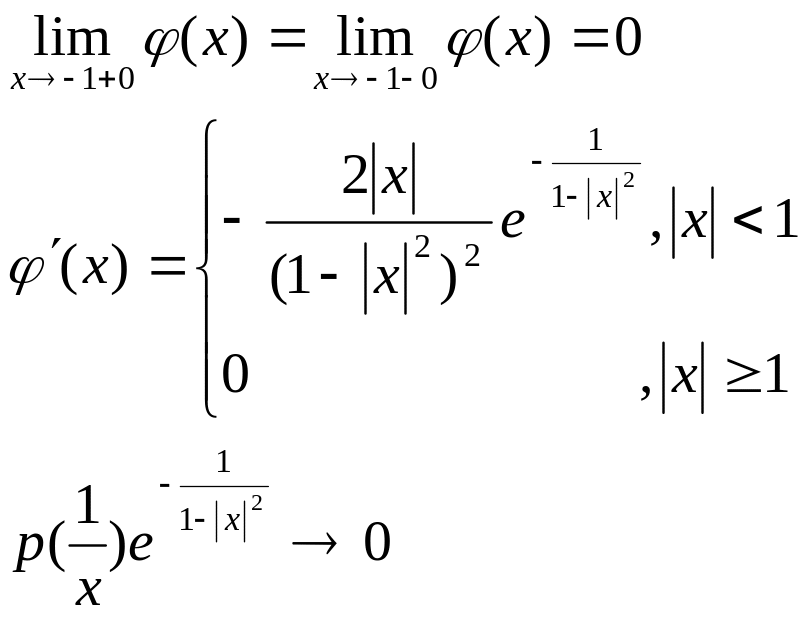
№54 Понятие обобщенной производной

Пусть обобщ. ф-ция опр-ся след. образом фиксированного: . Рассм-м ее производную:

Тогда k-я производная опред-ся: . Эту ф-лу обобщаем на все ф-ции. Обобщенной производной k-го порядка от обобщенной ф-ции будем называть обобщенную ф-цию , определяемую рав-вом: . Т. о., всякая обобщ. ф-ция бесконечное число раз диф-ма.

Пример1 Найдем обобщ. произв. -ф-ции Дирака:

Пример2

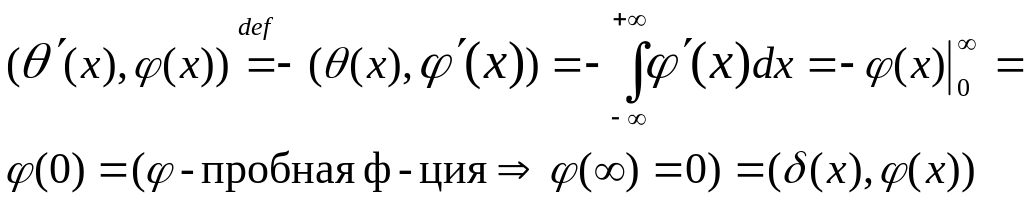
явл-ся производной классической ф-ции Хевисайда. Используя оператор диф-я, получим опр-ние :

Лемма Дробуа-Реймонда

Пусть , тогда - компакт, , можно указать мультииндекс и такую непрерывную ф-цию f(x) на этом компакте, что справедливо рав-во:

Выводы:

1. Всякая обобщенная ф-ция бесконечное число раз дифференцируема в обобщенном смысле.

На каждом компакте всякая обобщенная ф-ция есть обобщ. производная нек-рого порядка от нек-рой непрерывной ф-ции.

№55. Обобщенные и фундаментальные решения дифференциальных уравнений.

Пусть ζ=( ζ₁,…, ζ_n)єRⁿ

Pассмотрим полином P(ζ )=Σ _(|α|<=m)a_α ζ^α (1)

Рассмотрим соотв. дифференц. оператор P(D)=Σ_(|α|<=m)a_α D^α (2)

Рассмотрим в пр-ве обобщ. ф-ций уравнение P(D)*u(x)=f(x) (3) u,f є D’(Ω); f(x)-известна; u(x) надо найти;

Будем понимать произведение из левой ч.(3), как обобщ. произведение, т.е. (P(D)*u(x),φ(x))=( Σ_(|α|<=m)a_α D^α ,φ)=(u(x), Σ _(|α|<=m)a_α (-D^α )φ)=(u(x),P^*(D)φ)

P^*(D)-оператор формально-сопряженный к оператору P(D); Уравнение (3) понимается в след. смысле: (u, P^*(D)φ)=(f,φ) (4) для люб. φєD(Ω)

Опр. Обобщ. функцию u(x) будем называть обобщенным решением уравнения (3), если она удовлетв. тождеству (4) для люб. пробной функции φєD(Ω).

Следует выделить класс обобщ. решений

Если f(x)=δ(x), т.е. уравнен. (3) – P(D)*u(x)= δ(x)

(u(x), P^*(D)φ(x))=(δ(x),φ(x))=φ(0) т.о. обобщ. решение н-ся фунд-ным решением и обычно обознач. E(x)

№56. Cвертка и ее свойства

Опр. Сверткой 2-х классич. ф-ций f(x) и g(x) назыв. ф-ция (f*g)(x)=∫f(x-ζ)g(ζ)dζ

Rⁿ

при условии, что интеграл существует. Если f(x)=g(x)=1, то интеграл не существует. Одним из достаточных условии существования свертки яв-ся условие:

Пусть f(x)- непрер., g(x)-непр. и имеет компактный носитель, тогда свертка существует

С-ва свертки:

1. коммунитативность f*g=g*f

2. ассоциативность (f*g)*α=f*(g*α)

3. дистрибутивность D^α(f*g)=f*( D^αg)=( D^α f)g

Пусть Т- регулярная обобщенная ф-ция єD’(Rⁿ). Рассмотрим свертку обобщ. и пробной. (T*φ)(x)= ∫T(x-ζ)φ(ζ)dζ= ∫T(ζ)φ(x-ζ)dζ=(T(ζ),φ(x-ζ))

Rⁿ Rⁿ

По опред. считаем, что (T*φ)(x)= (T(ζ),φ(x-ζ))

Иногда можно определить и свертку 2-х обобщ. функции . Например T*δ=T - данное равенство имеет место только для обобщ. ф-ций (для классич. нет)

Рассмотрим в Rⁿ уравнение:

P(D)*u(x)=ψ(x) (1)

ψ(x)=C₀^∞ понимается в обычном классическом смысле

Лемма: Одним из классич. решений уравнения (1) является ф-ция вида :

u=(E*ψ)(x), где E(x)- фундам. решение оператора P(D): P(D)E(x)=δ(x), т.е. находя классич. решение нельзя обойтись без обобщ. функ-ции.

Д-во:

P(D) действует по переменным х, т.е. P(D_x). Подставим в свертку:

P(D_x)*(E*φ)(x)= P(D_x)*(E(f), φ(x-ζ))=(E(f), P(D_x)*ψ(x-ζ))=| ∂/∂xψ(x-ζ)=-∂/∂ζ ψ(x-ζ)|=(E(f),P(-D_ζ) ψ(x-ζ))= (P(-D_ζ)*E(f), ψ(x-ζ))=(δ(ζ), ψ(x-ζ))= ψ(x-ζ)|_ζ=0= ψ(x)

№57. Эллиптические уравнения. Постановка основных задач.

Будем считать х=(х₁,…,х_n)єRⁿ-ограниченная односвязная область Г=∂Ω

Оператор Лапласа Δu=∑_i=1ⁿ∂²u/∂x_i²

Ур-ние Пуассона : Δu=f(x) (1) стационарное, т.е. описывает процессы, установившееся во времени (зависит только от координат).

f-задача, х- найти

Ищем решение ур-ния в классич. смысле. Если Δu=0 – Ур-ние Лапласа

n=1=> лин. ф-ция.

Будем считать n=2.

Опр. Ф-ция u(x), дважды непрер. дифферен. в области Ω наз. гармонической ф-цией (опр-ной областью Ω), если она удовлетвор. уравнению Лапласа в этой области .

Для ур-нения Пуассона (1) (и для ур.Лапласса) на границе обл. Ω ставится одно из след. краевых условии:

1). u|_Г=φ(x) (2)

2). ∂u/∂n|_Г=ψ(x) (3)- задано знач-ние производной по направлению внешней нормали.

3). (αu+∂u/∂n) |_Г=h(x) (4)

Усл. (2) наз. краевым условием 1-го рода или условием Дирихле. Усл.(3) наз. краевым условием 2-го рода или условием Неймона. Усл. (4) наз. краевым условием 3-го рода .

Уравнение (1) с гранич. услов. (2), (3) или (4) наз. соответственно задачей Дирихле, внутр. зад. Неймона, внутренней зад. 3-го рода.

Рассмотрим случай, когда обл. Ω-неогранич., тогда к ур-нению Пуассона (1) с краев. условиями (2), (3) или (4) добавляют усл-вия регулярности на ∞:

{ 0(1), x→∞, n=2

u(x)= {

{ 0(1), x→∞, n>=3 (равном. стремится к 0)

№58. Некоторые свойства оператора Лапласа. Первая и вторая формулы Грина для оператора Лапласа.

Теорема: Пусть Ω– ограниченная область в , которая имеет кусочно-гладкую границу ∂Ω. Пусть ф-ии , , , , , , тогда определена формула: , где . (1) – первая формула Грина для основного оператора мат. физики.

Переобозначим u=v и рассмотрим разность: - вторая формула Грина. Если k(x)≡1,g(x)≡0, то Lu=∆u. Первая формула Грина: . Вторая формула Грина: .

№59. Следствия из формулы Грина.

Следствие1. Единственность решения внутренней задачи Грина для уравнения Пуассона . Решение внутренней задачи Грина (если оно сущ-ет) единственно с точностью до константы.

Док-во: Пусть u₁(x) и u₂(x)-2 решения. Рассмотрим ω(x)= u₁(x)- u₂(x), тогда . . . Используя первую формулу Грина : . доказано.

Следствие2. (необходимое условие разрешимости внутренней задачи Грина).

. Воспользуемся первой формулой Грина . –необходимое условие разрешимости внутренней задачи Грина. Отметим, что если условие имеет вид: . Замечание. Необходимое условие является и достаточным.

№60. Фундаментальное решение оператора Лапласа.

В уравнении с постоянными коэффициентами всегда ищут фундаментальное решение. Обобщенная функция называется фундаментальным решением оператора с постоянными коэффициентами p(D), если справедливо: . . .(т. е. оператор самосопряжен). Определение примет вид: (1). .

Свойства фундаментального решения:

1. Для любой точки x≠0 справедливо: .

2. Фундаментальное решение оператора Лапласа определяется с точностью до гармонической во всем Rⁿ функции Другими словами, если E(x)–фундаментальное решение, h(x)- гармоническая функция, то E₁(x)=E(x)+h(x) также будет фундаментальным решением.

Док-во: . Доказано.

3. Пусть – фиксированный вектор, тогда . (самост. д-ть).

Предположения.

1). Фунд. решение является регулярной обобщенной ф-ей, т. е. определяется обычной классической ф-ей E(x), определенной всюду, кроме начала координат .

2). Везде, кроме точки х=0 ф-ия E(x) гармоническая, т. е. удовлетворяет уравнению Лапласа .

3). Оператор Лапласа всякую радиальную функцию (т. е. ) переводит в радиальную.

Потребуется ввести специальную систему координат.

при n=2

Обобщаем при n≥3 ,

- радиальная часть оператора Лапласа.

Оператор – угловая часть оп-ра Лапласа( оп-ор Лапласа-Бельтрати)

Случаи n=2, n=3 входят как частные случаи.

В силу третьего предположения:

const является гармонической ф-ей. След-но, ее можно отбросить . Докажем, что предположения верны и найдем const. Для этого воспользуемся определением: (1). Покажем, что для любой дробной ф-ии справедливо следующее равенство. Отметим, что :

1. Ф-ия

2. (К-компакт)

Из этого свойства получаем, что фундаментальное решение является регулярной функцией.

3.

( 1) понимается в следующем смысле: . –шар радиуса с центром в начале координат.

Воспользуемся второй формулой Грина для оператора Лапласа . Применяем к нашему равенству: Отметим, что область интегрирования ограничена, т. к. φ–пробная ф-ия, т. е. имеет компактный носитель.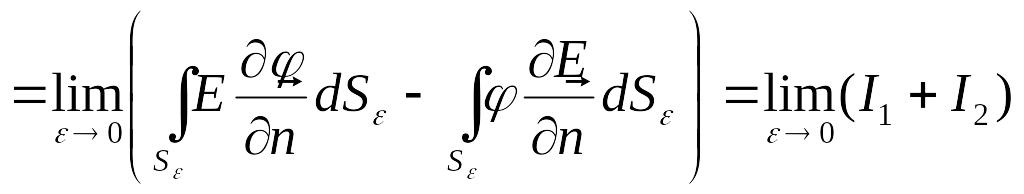 (2)

=

. Фундаментальное решение является радиальной ф-ей(т. е. const, которую можно вынести за знак интеграла).

n≥3 =

n=3

. Точка . .

Продолжая (2): . Выпишем формулу фундаментального решения: .

Замечания: При док-ве ф-лы фунд-го решения мы не пользовались бесконечной дифференцируемостью. Сл-но, рав-во (1) справедливо для финитной дважды непрерывно дифференцируемой ф-ии .

Пусть дано уравнение: ( f(x)- финитная двады непр. диф.). Тогда одним из классич. реш-ий этого ур-ия явл-ся ф-ия: .

Док-во: Нужно взять произвольную пробную функцию, рассмотрим свертку:

. Доказано.

№61. Физический смысл фундаментального решения оператора Лапласа.

Два заряда q₁,q₂ помещены в R³, на них действует сила –закон Кулона. Выбираем систему координат таким образом, чтобы q₁ оказался в начале координат и возьмем q₁=q₂=1. Тогда сила, с которой заряды действуют друг на друга: .q₁ оставляем на месте, а q₂ будем перемещать в произвольную точку. R³\{0}. В этом случае сила F, действующая на заряд будет силой в точке: . Т. о. мы задали некоторое векторное поле. В физике оно называется электростатическим полем, порождаемым единичным зарядом q₁, помещенным в начало координат. Силу , с которой q₁ действует на q₂, находящийся в точке x наз. напряженностью электростатического поля. Векторное поле является потенциальным, т. е. ; . , тогда , если R³. Т. о. физический смысл фундаментального решения оператора Лапласа, это потенциал электростатического поля, порождаемый единичным зарядом, помещенным в начало координат. Единичный заряд q₁, помещенный в начало координат в терминах потенциала электростатического поля может быть записан в виде уравнения: .

N62. Интегральное представление функции Лапласа.

Пусть - огранич. обл-ть из , - кусочно-гладкая. Рассмотрим ф-ю . Предположим, что известно 1) значения внутри обл-ти

2) значения на границе ;3) значения на границе .

Задача По этим данным восстановить знач. ф-ции U в кажд. т. . Это задача о нахожд. интеграл. представления. Нам известно, что если U(x) явл-ся финитной,то зад-ча имеет след. решение: . В общем случае U(x) не обязательно финитная.

Теорема Пусть ф-я . Тогда справ-во рав-во

(1)

док-во Отметим, что (1) можно переписать в эквив. виде (фунд. реш. явл-ся радиальн. ф-цией ; ; Выберем сис-му коорд., чтобы т х. была в начале координат. Тогда эквивал-но перепис-ся в виде :

; Докажем . Отметим,что ; ; Фун-ю U представим в виде : ; ф-я v(x) финитная :

Тогда справ-во рав-во ( свертка) ;v(0)=U(0)

(2); Расс-м ф-цию ,исп-я 2-ю форумулу Грина :

; Возьмем U=E; v= и получим след. ра-во

; Отметим,что ; Тогда интеграл в левой части рав-ва берется по областям:

(Лапл. явл-ся гармон. ф-цией Если достат. мало.то на границе Г обл-ть ,поэтому получаем рав-во

(3) Сложим рав-ва (2) и (3)

теорема доказана

Замечание 1.При док-ве фор-лы (1) мы нигде не пользовались бескон. диф-ю ф-ции U(x), поэтому (1) справ-во и в случае , когда U(x) явл-ся дважды-непрер. дифференц. в обл-ти и один раз в ,т.е Заметим также, что нам не нужно даже требовать того,чтобы сама фун-я U и была определена на границе, достат. потребовать, чтобы сущ-ли пределы:

; в дальнейшем гран. условия понимаем именно в таком роде

Замечание 2. Интегральное представление справ-во лишь для внутр. точек . Для гран. точек оно теряет силу. Но известен след. рез-т:

В последнем случае инт-лы понимаются неот-ные.

№63. Свойства Гармонических функций.

Фун-я наз-ся гармонич. в огранич. обл-ти, если

1. Бесконечная дифференцируемость .

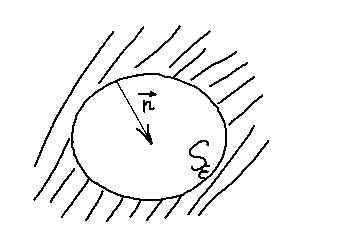
Теорема если ф-ция U(x) гармонич. в обл-ти ,то . Док-воЗафиксируем произв. . Тк. Х – внутр. точка из ,то она входит вместе с нек-й окр-ю ; если . Тогда для нее справедливо интег-е представл-е:

Заметим,что в инт-ле пробегает , а т. х- внутр. точка мн-ва D всегда; ф-ции ( по х) Они явл-ся пар-ми; мы можем менять местами операции инт-я по перем-й и дифф-я по пар-ру х, причем диф-ть мы можем любое число раз.

2. Теорема о потоке тепла – граничное св-во гармонич. Ф-ции;

Если U(x) –гармон. ф-я в огранич. обл-ти и gradU(x) 1 раз непрер.-диф. в , то

Это св-во было док-но как следствие формул Грина и наз-ся необх. усл. разрешимости зад-чи Неймона для ур-ния Лапласа; Теорема о потоке тепла имеет физ. интерпретацию: Если U(x) задает стацион. распр-е темпер. внутри однородной изотропной среды, заполняющей объем , то с точностью до пост. множ-ля, завис-го от выбора единиц измерения задает поток тепла через пов-ть в сторону нормали . Теорема о потоке утв-т,что поток тепла через границу тела при стац. распред. темпер. равен 0. Следствие : Пусть постоянные таковы что шары, содержащ-ся вместе со своим замыканием в обл-ти .

Будем считать, что . Применим теор. о потоке тепла в обл-ти

Тогда граница обл-ти сост. из 2-х сфер радиусов . Мы получим :

; возьмем - фундам. реш-е:

; Это рав-во означ., что кол-во тепла, проход. через любую сферу с центром в т. в направлении внешней нормали при распред-нии температуры в соот. ф-ции , постоянно, поэтому в т. при распред-нии температуры можно рассма-ть как источник тепла, выдел. кол-во тепла равное :

3. Связь аналитических и гармонических функций.

Теорема. Для того, чтобы функция f (z)= u(x, y) + i*v(x, y) была дифференцируемой в т.(х,у) н. и д., чтобы функции u(x, y) и v(x, y) были дифференцируемы в т. (х,у); в т. (х,у) должно выполняться условие Коши-Римана

(1)

Пусть функция f(z) дифференцируема в области D и кроме того функции u(x, y) и v(x, y) имеют непрерывные частные производные до 2-го порядка включительно. Тогда дифференцируя первое равенство по х, а второе по у, мы получим

Учитывая, что = , получим (2)

Т.е. u – гармоническая, аналогично, функция v – гармоническая.

Поэтому действительные и мнимые части функции f(z) являются гармоническими функциями в этой области.

Опр. Гармонические функции u(x, y) и v(x, y), связанные между собой условиями Коши-Римана, называются сопряжёнными, т.е. действительная и мнимая части дифференцируемые в области функции являются в этой области сопряжёнными гармоническими функциями.

Обратно, если в области D даны две сопряжённые гармонические функции u(x, y) и v(x, y), то по теореме 1 функция f(z) дифференцируема в области D, т.е. справедлива

Теорема: Для дифференцируемости функции f(z)= u(x, y) + i v(x, y) н. и д., чтобы функции u(x, y) и v(x, y) были сопряжёнными гармоническими функциями в этой же области D.

Зная одну из функций u(x, y) или v(x, y), можно в односвязной области найти другую функцию.

Теорема: Для всякой функции u(x, y) гармонической в односвязной области D можно найти сопряжённую с ней гармоническую функцию, которая определяется с точностью до произвольного постоянного слагаемого.

Док-во:

Т.к. u(x, y)- гармоническая функция, то и следовательно выражение является полным дифференциалом некоторой однозначной функции v(x, y), определяемой с точностью до произвольного слагаемого формулой

v(x, y)= + +С (3)

Здесь (x_о, y_о) D и (x_, y) D, интеграл не зависит от кривой, соединяющей точки (x_о, y_о) и (x_, y), а зависит только от точки (х,у), при условии, что (х₀,у₀) – фиксированная.

Из равенства (3) получаем

Откуда следует, что v(x, y) – гармонич. в области D функция, сопряжённая с u(x, y). Теорема доказана.

Из т. 2 и т. 3 следует, что если задана гармоническая функция u(x, y) в односвязной области D , то с точностью до постоянного слагаемого мы можем определить функцию f(z), дифференцируемую в D, f(z)=u(x,y)+i*v(x,y).

Т.е. восстановить дифференцируемую функцию по заданной её действительной (мнимой) части.

Если D – многосвязная область, то функция v(x,y) из формулы (3), а также f(z) могут оказаться неоднозначными.