18.Применение теории вероятностей к расчетам колебаний годового стока.

Теория вероятностей позволяет устранить недостатки эмпирической кривой обеспеченности.

Один из методов теории вероятностей к исследованию гидрологических явлений является кривая распределения или кривая обеспеченности, которая дает в общей форме характеристику распределения того или иного гидрологического элемента за период наблюдений.

И что особенно важно, она при современном уровне гидрологических знаний является единственным основанием для суждения о вероятности появления в будущем гидрологического явления большого или меньшего по величине, чем любое заданное значение.

19.Понятие о кривых распределения и обеспеченности.

Кривые обеспеченностей дают возможность решить многие инженерные задачи такие как:

• рассчитать максимальный и минимальный притоки;

• установление размеров водосбросных отверстий плотин;

• определение расчетной мощности проектируемой гидроэлектростанции;

• разработка режимов регулирования стока водохранилищами,…

Кривые обеспеченности дают возможность сравнивать различные реки по одинаковым показателям ( ,к…), позволяют делать широкие гидрологические обобщения. И, чем длиннее ряд, тем надежнее расчеты.

С помощью кривой обеспеченности можно определить расход любой ЗАДАННОЙ обеспеченности в пределах данного периода наблюдений.

20.Параметры кривой распределения.

1. Центр распределения (а) – среднеарифметическое значение ряда;

2. Медиана (в) – соответствует 50% - ной обеспеченности;

3. Модуль кривой (с) – соответствует наибольшей частоте расходов.

В несимметричных кривых распределения (биноминальная кривая распределения) показателем асимметрии служит величина d, называемая радиусом асимметрии, представляющая собой расстояние между модой и центром распределения.

21.Параметры кривой обеспеченности.

1. Средний расход ряда 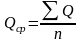, где Q - сумма всех расходов данного ряда, n -общее число членов (расходов) ряда.

2. Коэффициент вариации (характеризует изменчивость случайной величины во времени и пространстве). Другими словами, 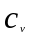есть нормированное среднее квадратическое отклонение случайной величины.

а) для короткого ряда

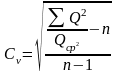
б) для длинного ряд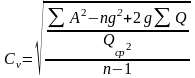а , где g - постоянное число, на

которое уменьшается каждая величина Q; А=Q-g.

Отдельные значения параметра А ряда могут быть отрицательными, или равными нулю. Таким образом, коэффициент вариации или изменчивости годового стока, служит мерой оценки колебания годового стока относительно его нормы.

3. Коэффициент асимметрии характеризует степень несимметричности ряда рассматриваемой случайной величины относительно ее среднего значения и вычисляется по формуле

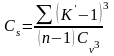
Кривая обеспеченности симметрична когда C_s =0; если сумма кубов отклонений членов ряда (одной ветви кривой) больше суммы кубов для другой ветви – кривая обеспеченности асимметрична.

Для биноминальной асимметричной кривой обеспеченности коэффициент асимметрии заключается в пределах от C_s = 2 C_v до ,

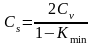К_min – наинизший модульный коэффициент

В практике принято при расчетах среднего годового стока соотношения

C_s = 2 C_v, т.к. в жизни длинные ряды редки.