14. Определение нормы годового стока при отсутствии гидрометрических наблюдений.

Рекомендуются два приема определения нормы годового стока при отсутствии гидрометрических наблюдений:

- интерполяцией по картам изолиний среднего многолетнего стока основанных на территориальной интерполяции гидрометеорологических данных.

- интерполяцией стока между опорными пунктами с установленными для них значениями нормы.

По данным Б.Д.Зайкова и С.Ю.Беликова, средняя ошибка нормы годового стока малых рек по карте в сравнении с наблюдаемой нормой составляет около ±15% для северных и центральных районов ЕТС и около ±20% для южных районов; для больших рек эта ошибка равна соответственно ±8% и ±10%.

Для определения нормы стока по карте изолиний, площадь бассейна до рассматриваемого створа должна быть оконтурена по водоразделам и определен её центр как точка пересечения прямых линий, делящих бассейн на две, примерно равные части (см. рис 2).

Точка пересечения прямых является как бы геометрическим центром водосбора. Модуль стока для полученного центра бассейна определяется по прямолинейной интерполяции между ограничивающими бассейн изолиниями. А более точно модуль стока определяется как средневзвешенный по формуле:

;

где M₁ и M_n - средние арифметические величины модулей стока по изолиниям, ограничивающим рассматриваемые части бассейна;

f₁……f_n - площади бассейна между этими изолиниями стока.

Норма годового стока получается по формуле:

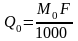(м³/сек)

где М₀ – модуль стока определенный по карте;

F_общ – площадь бассейна до рассматриваемого створа в км².

Частные площади определяются методом планиметрирования: первой (f₁) площади бассейна, второй (f₂) и их значения подставляются в формулу:

F_общ=f₁+f₂+…+f_n

15. Интегральная кривая стока и лучевой масштаб в прямоугольной системе координат.

Прямоугольные координаты W₂ - W₁=W

W=∫Q dt, отсюда следует Q=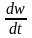 , т.е. для каждого момента времени расход выражается тангенсом угла наклона касательной к интегральной кривой к оси абсцисс (х).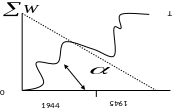

Участки кривой с крутыми подъемами соответствуют весенним периодам нарастания стока, более пологие – летним и зимним.

Тангенс угла , образованного прямой, соединяющей начало и конец интегральной кривой с осью абсцисс, характеризует средний расход за весь рассматриваемый период:

=Q_ср м³/сек,

а за конкретный период средний расход равен:

Qср=tg ,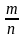

где m и n принятые масштабы в единицах измерения по вертикальной и горизонтальной шкале

Определение среднего расхода (или другой величины стока) за любой период времени по интегральной кривой удобно производить графическим способом, для чего строится специальный лучевой масштаб.

Лучевой масштаб можно построить за пределами графика.

Основание лучевого масштаба (Р), т.е. полюсное расстояние, можно определить по формуле: см,

где m_w – число единиц в 1 см. вертикального масштаба для суммарного стока ΣW.

m_Q – число единиц в 1 см. вертикального масштаба для расходов Qм³/сек.

m_т - число единиц в 1 см. горизонтального масштаба за время Тсек.

Подставляя в формулу приведенные величины, мы получим длину полюсного расстояния Р, которое и откладываем слева или справа от графика. По ординате откладываем значения величин (Q,W) в принятом масштабе и, соединив их с точкой полюса, получим пучок лучей веера.