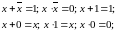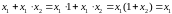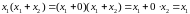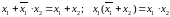Законы и тождества алгебры логики

1. Двойное отрицание.

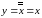
0	1	0
0	0	1

2. Закон повторения.

0	0	0
1	1	1

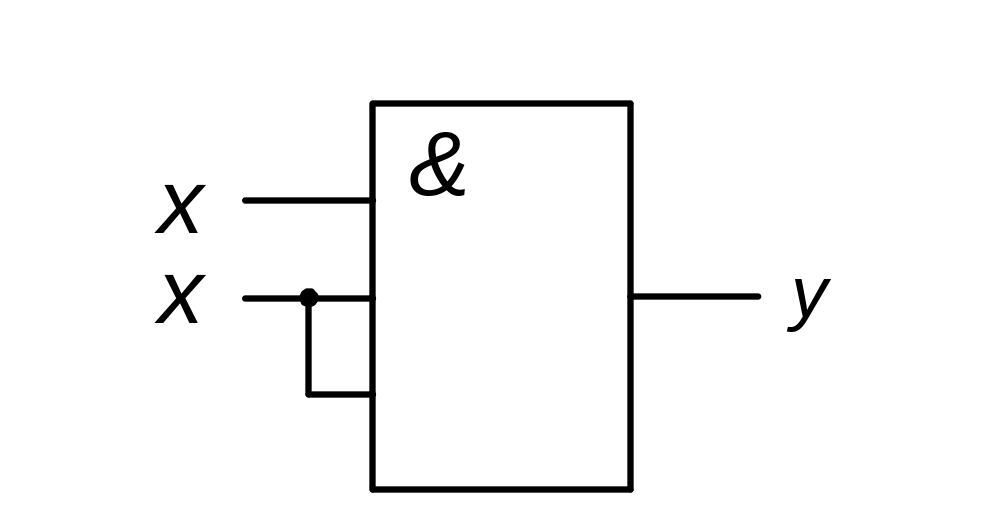
3. П ереместительный закон.

0	0	0	0
0	1	0	0
1	0	0	0
1	1	1	1
0	0	0	0
1	0	1	1
0	1	1	1
1	1	1	1

4. Сочетательный закон.

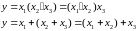
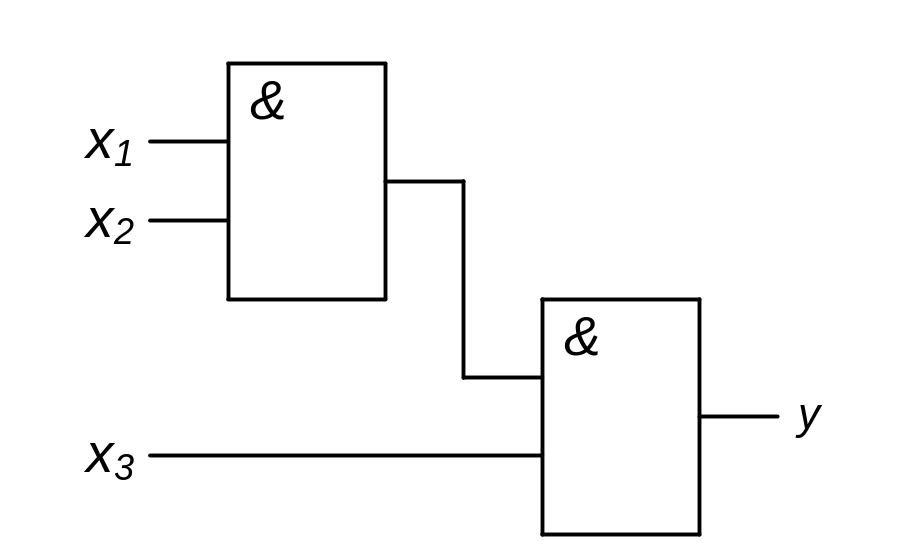
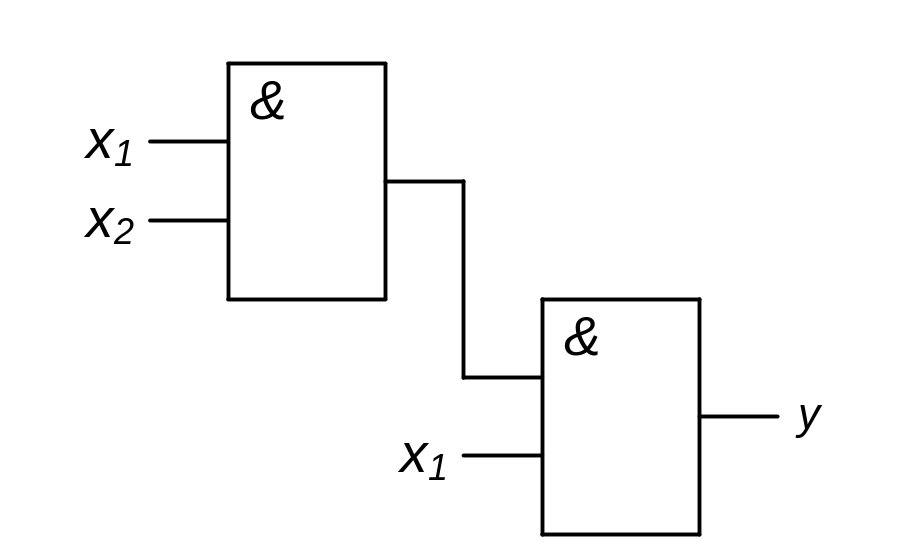
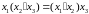
5. Распределительный закон

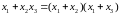
0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0
0	1	0	1	0	0	0	0
1	1	0	1	1	0	1	1
0	0	1	1	0	0	0	0
1	0	1	1	0	1	1	1
0	1	1	1	0	0	0	0
1	1	1	1	1	1	1	1

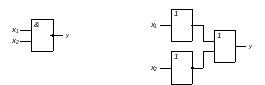
6. Закон инверсии операции (закон Де Моргана)

0	0	1	1	0	1	1
1	0	0	1	0	1	1
0	1	1	0	0	1	1
1	1	0	0	1	0	1

Тождества алгебры логики

1. 

2. 

3. 

4. 

Способ перехода от словесного описания к алгебраической записи.

Переход возможен на основании 2-х вариантов:

1. СНДФ (совершенная дизъюктивная нормальная форма).

Дизъюнкция – операция «ИЛИ».

2. СКДФ (совершенная конъюктивная нормальная форма).

Конъюнкция – операция «И».

Правило перехода от таблицы истинности к символической записи.

1. Обозначим истинное значение функции через , а ложное значение функции через .

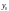2. Если переменная в таблице имеет значение «0», то в аналитической записи она записывается со знаком отрицания.

3. Все переменные одной строки соединяются символом конъюнкции ( ).

4. Между собой члены общей аналитической записи соединяются символом дизъюнкции (+).

5. Для записи функции , т.е. истинного значения функции, используются все сроки таблицы, в которых, принимает значение «1».

6. Для записи используются все сроки таблицы, в которых принимает значение «0».

34