
- •Теория рядов числовые ряды
- •Основные понятия
- •Свойства сходящихся рядов
- •3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
- •6. Над сходящимися рядами можно выполнять арифметические действия: сложение, вычитание, умножение, деление. Они выполняются как действия над многочленами.
- •2. Необходимый признак сходимости ряда (теорема).
- •3. Знакоположительные ряды. Признаки сходимости знакоположительных рядов
- •3.1. Первый признак сравнения
- •3.2. Второй признак сравнения (предельный признак)
- •1) , , Т. Е. Члены ряда не возрастают (убывают) по абсолютной величине;
- •2) , То данный ряд сходится, а его сумма не превосходит первого члена ряда, т. Е. .
- •5. Абсолютная и условная сходимость знакопеременного ряда
- •Свойства абсолютно сходящихся рядов
- •1. Перестановка членов абсолютно сходящегося ряда не нарушает его сходимости.
- •2. Если и – абсолютно сходящиеся ряды с суммами и соответственно, то ряд: также абсолютно сходящийся, а сумма его равна .
- •3. Если и – абсолютно сходящиеся ряды с суммами и соответственно, то ряд также абсолютно сходящийся с суммой . Свойства условно сходящихся рядов
- •Глава 2. Функциональные ряды
- •5. Функциональные ряды. Степенные ряды
- •Свойства степенных рядов
- •1. Если радиус сходимости степенного ряда (1) отличен от нуля, то его сумма непрерывна на интервале сходимости .
- •3. Внутри интервала сходимости ряды можно складывать, вычитать, умножать, делить, умножать на число. Интервал сходимости должен быть общим для этих рядов.
- •6. Ряды Тейлора и Маклорена
- •Признак разложимости функции в ряд Тейлора.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •7. Разложение элементарных функций в ряд
- •1) Функция вида
- •. Приложения степенных рядов
- •8.1. Приближённое вычисление значений функции
- •8.2. Приближённое вычисление определённых интегралов
- •8.3. Приближённое решение дифференциальных уравнений
. Приложения степенных рядов
8.1. Приближённое вычисление значений функции
Задача.
Найти
приближенное значение функции
в точке
 с заданной степенью точности
с заданной степенью точности
 .
.
Решение.
Разложим
функцию
в ряд по степеням
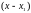 с интервалом сходимости, содержащим
точку
с интервалом сходимости, содержащим
точку
 ,
где
,
где
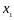 – точка, в которой значения функции, а
также её производных легко вычисляются,
давая точные значения.
– точка, в которой значения функции, а
также её производных легко вычисляются,
давая точные значения.
Переменной
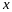 даем значение
даем значение
 и в числовом ряду
и в числовом ряду
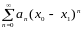 оставим только те члены, которые
гарантируют заданную точность.
оставим только те члены, которые
гарантируют заданную точность.
Число таких членов определяется по правилу:
– если
ряд знакоположительный, то с помощью
остаточного члена
 формулы Тейлора
формулы Тейлора
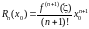 ,
,

– если
ряд знакочередующийся, то с помощью
остатка
 ряда Тейлора
ряда Тейлора
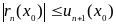 .
.
Пример.
Вычислить
 с точностью
с точностью
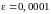 .
.
Решение.
Имеем
 и
и
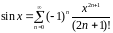 – знакочередующийся ряд, значит,
применим остаток ряда Маклорена.
– знакочередующийся ряд, значит,
применим остаток ряда Маклорена.
 ,
,
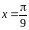 ,
,
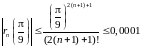 ,
,
 .
.
Подбором,
при значении
 получим
получим
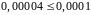 – условие выполняется. Тогда,
– условие выполняется. Тогда,
 .
.
Пример.
Вычислить
 с точностью
с точностью
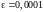 .
.
Решение.
Для
вычисления
 запишем ряд
запишем ряд

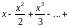
 .
При
.
При
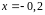 ,
входящем в область сходимости ряда
,
входящем в область сходимости ряда
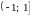 :
:
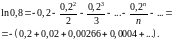
Если
в качестве
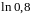 взять первые четыре члена, мы допустим
погрешность
взять первые четыре члена, мы допустим
погрешность
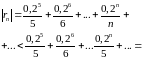
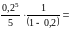
 .
.
Итак,
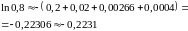 .
.
Пример.
Вычислить
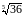 с точностью
с точностью
 .
.
Решение.
Представим
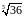 в виде
в виде
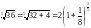 .
Так как
.
Так как
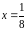 входит в область сходимости степенного
ряда
входит в область сходимости степенного
ряда
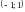 ,
то при значениях
,
то при значениях
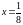 ,
,
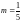 ,
учитывая, что
,
учитывая, что
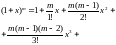
 ,
получим:
,
получим:
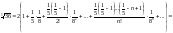
 .
.
Для
обеспечения данной точности расчета
необходимо взять 4 члена, так как по
следствию из признака Лейбница для
сходящегося знакочередующегося ряда
погрешность
 .
.
8.2. Приближённое вычисление определённых интегралов
Многие определенные интегралы, не выражающиеся в элементарных функциях, могут быть вычислены с помощью рядов. Отрезок интегрирования должен находиться внутри интервала сходимости ряда.
Пример.
Вычислить
интеграл
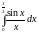 c точностью
c точностью
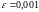 .
.
Решение.
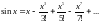 ,
,
 ,
,
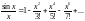 ,
,
отсюда
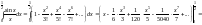
 .
.
Вычисляя
члены этого ряда с точностью
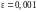 ,
замечаем, что третий член ряда по
абсолютной величине меньше
,
замечаем, что третий член ряда по
абсолютной величине меньше
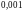 .
Следовательно, для решения этой задачи,
согласно признаку Лейбница, надо взять
сумму первых двух членов, что обеспечит
требуемую точность
.
Следовательно, для решения этой задачи,
согласно признаку Лейбница, надо взять
сумму первых двух членов, что обеспечит
требуемую точность
 .
.
8.3. Приближённое решение дифференциальных уравнений
Если решение дифференциального уравнения не удаётся найти в элементарных функциях, то для их решения можно применять степенные ряды.
Пример.
Найти
первые три (отличные от нуля) члена
разложения в ряд Маклорена функции
 ,
являющейся частным решением
дифференциального уравнения
,
являющейся частным решением
дифференциального уравнения
 ,
если
,
если
 .
.
Решение.
Положим,
что
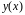 является решением данного дифференциального
уравнения при указанных начальных
условиях. Если
является решением данного дифференциального
уравнения при указанных начальных
условиях. Если
 допускает разложение в ряд Маклорена,
то имеем
допускает разложение в ряд Маклорена,
то имеем
 .
.
Свободный
член разложения, т. е.
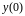 ,
дан по условию. Чтобы найти значения
,
дан по условию. Чтобы найти значения
 ,
можно данное уравнение последовательно
дифференцировать по переменной
,
можно данное уравнение последовательно
дифференцировать по переменной
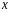 и затем вычислить значения производных
при величине
и затем вычислить значения производных
при величине
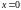 .
.
Значение
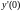 получаем, подставив начальные условия
в данное уравнение:
получаем, подставив начальные условия
в данное уравнение:
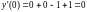 ,
т. е.
,
т. е.
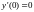 .
.
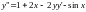 ,
,
 ,
т. е.
,
т. е.
 .
.
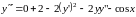 ,
,
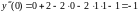 ,
т. е.
,
т. е.
 ,
…
,
…
Подставив
найденные значения производных при
значении
в ряд
 ,
получим разложение искомого частного
решения уравнения в ряд:
,
получим разложение искомого частного
решения уравнения в ряд:
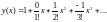 .
.
Окончательно,
 .
.
