40. Электромагнитные колебания. Колебательный контур. Добротность колебательного контура. Период электромагнитах колебаний в контуре. Получение электромагнитных волн. Излучение электрического диполя.

Электромагнитными колебаниями называются периодические изменения напряженности Е и индукции В. Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

Электромагнитные волны как универсальное явление были предсказаны классическими законами электричества и магнетизма, известными как уравнения Максвелла.

Колебательный контур – замкнутая электрическая цепь, состоящая из последовательно соединенных катушки индуктивности и конденсатора.

Колебательный контур — осциллятор (осцилля́тор — система, совершающая колебания, то есть показатели которой периодически повторяются во времени), представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

К олебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.

Резонансная частота контура определяется так называемой формулой Томсона:

Резонанс токов означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют.

Период – минимальный промежуток времени, через который процесс повторяется.

Простейшим излучателем электромагнит­ных волн является электрический диполь, электрический момент которого изменяет­ся во времени по гармоническому закону

р = р₀cost,

где р₀ — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительно­го заряда +Q и отрицательного заряда -Q, гармонически колеблющегося вдоль направления р с частотой .

Задача об излучении диполя имеет в теории излучающих систем важное зна­чение, так как всякую реальную излучаю­щую систему (например, антенну) можно рассчитывать рассматривая излучение ди­поля. Кроме того, многие вопросы взаимо­действия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармони­ческие колебания около их положений равновесия.

Характер электромагнитного поля ди­поля зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя — точ­ки пространства, отстоящие от диполя на расстояниях r, значительно превышающих длину волны (r>>),— так как в ней кар-

тина электромагнитного поля диполя силь­но упрощается. Это связано с тем, что в волновой зоне диполя практически оста­ются только «отпочковавшиеся» от дипо­ля, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области рас­стояний r<=.

В основе теории Максвелла лежат рас­смотренные выше четыре уравнения:

1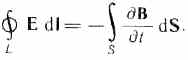 . Электрическое поле мо­жет быть как потенциальным (e_q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е_Q+Е_B. Так как циркуляция вектора e_q равна нулю, а циркуляция вектора Е_B оп­ределяется выражением, то цир­куляция вектора напряженности суммар­ного поля:

2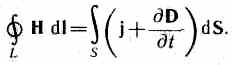 . Обобщенная теорема о циркуляции вектора Н:

Это уравнение показывает, что магнит­ные поля могут возбуждаться либо дви­жущимися зарядами (электрическими то­ками), либо переменными электрическими полями.

3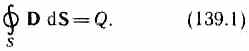 . Теорема Гаусса для поля D:

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью , то формула запишется в виде:

4. Теорема Гаусса для поля В :

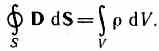
41. Энергия электромагнитных волн. Импульс электромагнитного поля. Вектор плотности потока энергии.

Энергия электрического и магнитного полей:

плотности энергии электрического и маг­нитного полей в каждый момент времени одинаковы, т. е. w_эл = w_м. Поэтому

Умножив плотность энергии w на скорость v распространения волны в среде, получим модуль плотности потока энергии:

Tax как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпада­ет с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга:

Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

w- энергия с- скорость света p=W/c - импульс электромагнитного поля p-импульс W- энергия

c-ск.света