34. Получение переменного тока. Устройство генератора переменного тока. Амплитудное и действующее значения напряжения и силы тока.

Получение переменного тока

Генератор переменного тока

Системы производящие переменный ток были известны в простых видах со времён открытия магнитной индукции электрического тока. Ранние машины были разработаны такими пионерами, как Майкл Фарадей и Ипполит Пикси.

Фарадей разработал «вращающийся треугольник», действие которого было многополярным — каждый активный проводник пропускался последовательно через область, где магнитное поле было в противоположных направлениях. Первая публичная демонстрация наиболее сильной «альтернаторной системы» имела место в 1886 году. Большой двухфазный генератор переменного тока был построен британским электриком Джеймсом Эдвардом Генри Гордоном в 1882 году. Лорд Кельвин и Себастьян Ферранти также разработали ранний альтернатор, производивший частоты между 100 и 300 герц. В 1891 году Никола Тесла запатентовал практический «высокочастотный» альтернатор (который действовал на частоте около 15000 герц). После 1891 года, были введены многофазные альтернаторы.

Принцип действия генератора основан на явлении электромагнитной индукции — возникновении электрического напряжения в обмотке статора, находящейся в переменном магнитном поле. Оно создается с помощью вращающегося электромагнита — ротора при прохождении по его обмотке постоянного тока. Переменное напряжение преобразуется в постоянное полупроводниковым выпрямителем.

Амплитудное и действующее значения напряжения и силы тока

35. Переменный ток. Активное сопротивление в цепи переменного тока. Графическое изображение переменного тока. Векторная диаграмма.

Переме́нный ток(англ. alternatingcurrent — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.

Активное сопротивление

Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.

К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.

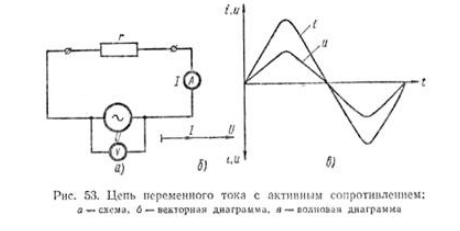
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.

Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.

Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (j=0), откладываем вектор тока I по направлению вектора напряжения.

Сила тока в такой цепи определяется по закону Ома:

В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.

Графическое изображение переменного тока

Рассмотрим подробнее кривую, изображающую зависимость мгновенного значения технического переменного тока (или напряжения) от времени (рис. 293). Прежде всего обращает на себя внимание тот факт, что этот ток (или напряжение) изменяется периодически, т. е. каждое мгновенное значение этих величин, например значение, соответствующее точке а (или точке b), повторяется через один и тот же промежуток времени. Другими словами, сила тока (или напряжение) пробегает за этот промежуток времени все возможные значения, возвращаясь к исходному, т. е. совершает полное колебание. Промежуток времени, в течение которого сила тока (или напряжение) совершает полное колебание и принимает прежнее по модулю и знаку мгновенное значение, называется периодом переменного тока. Его принято обозначать буквой Т. Для сетей СССР и большинства других стран Т=1/50 с, а так как изменение направления тока происходит два раза в течение каждого периода, то технический ток меняет свое направление 100 раз в секунду. Максимальное значение, которое может иметь переменный ток (или напряжение) в том или другом направлении, называется амплитудой этой величины. На рис. 293 амплитуда изображается отрезками АА\'. Амплитуду токов и напряжений обозначают Im или Um, а их мгновенные значения — i и u.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний итд.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) - фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда - длиной этого вектора, а фаза - углом его поворота относительно Ox.

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy - оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).

Тогда вектор длиной A, вращающийся в комплексной плоскости с постоянной угловой скоростью ω с начальным углом φ₀ запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω и начальной фазой φ₀.