Вопросы-ответы.

1. Электрический заряд. Единицы электрического заряда. Взаимодействие электрических зарядов. Закон сохранения электрических зарядов. Плотность электрических зарядов. Закон кулона.

1) Электри́ческийзаря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии

2) е=1.6х10(-19) Кулон

3)Эл заряды могут притягиваться(разноименные) и отталкиваться(одноименные).

4) закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними тела­ми) остается неизменной, какие бы процессы ни происходили внутри этой системы.

5) Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма

6 )Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

2. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции. Графическое изображение электрических полей. Напряженность электрического поля точечного заряда.

1)Электрическое поле — особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом.

2)напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда.  (В/м)

3)При́нципсуперпози́ции — результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

4)Графическое изображение электрических полей

Силовые линии напряженности электрического поля - линии, касательные к которым в каждой точке совпадают с вектором Е

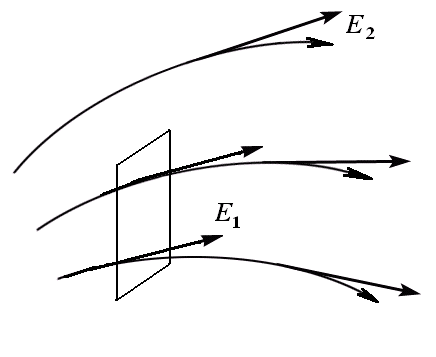
Направление вектора Е совпадает с направлением силы, действующей на положитель­ный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положи­тельного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 118).

5)напряженность эл.поля точечного заряда

3. Поток вектора напряженность. Теорема Гаусса. Применение теоремы Гаусса для расчета электрических полей: А) точечного заряда Б) бесконечно заряженной плоскости.

1) поток вектора напряженности через площадку dS. Здесь dS = dSn — век­тор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Единица потока вектора напряженности электростатического поля — 1 Вм.

2) Теорема Гаусса (закон Гаусса) — Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

3) А) для точечного заряда Б) бесконечно заряженная плоскость

4. Поток вектора напряженности. Теорема Гаусса. Применение теоремы Гаусса для расчета электрических полей. А) Равномерно заряженной сферической поверхности Б) объемно заряженного шара.

1) поток вектора напряженности через площадку dS. Здесь dS = dSn — век­тор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Единица потока вектора напряженности электростатического поля — 1 Вм.

2 ) Теорема Гаусса (закон Гаусса) — Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

3) А) Сферическая поверхность Б)для шара Е=ρR/3Ɛ˳

5. Работа по перемещению заряда в электрическом поле. Энергия взаимодействия точечных зарядов. Циркуляция вектора напряженности.

1) работа сил поля по перемещению эл. Зарядов вдоль замкнутого контура =0 Работа, совершаемая силами электростатического поля при перемещении заряда Q₀ из точки 1 в точку 2 может быть представлена как т.е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.

2)потенциальная энергия 2-х зарядов W=Q1*Q2/4πƐ˳r

3) Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

6. Потенциал поля. Разность потенциалов. Потенциал поля точечного заряда. Связь напряженности с потенциалом. Эквипотенциальные линии и поверхности. Вычисление разности потенциалов двух бесконечных параллельных разноименно заряженных плоскостей.

1)потенциал — физическая величина, определяемая работой по переме­щению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

2)Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду. В СИ единицей разности потенциалов является вольт (В).

3) 1)Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:   

4) Связь напряженности с потенциалом

5)Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков

6)Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой Е=σ/Ɛ˳,

где σ— поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d равна:

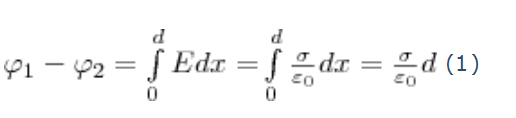d-расстояние между плоскостями

7. Проводники в электрическом поле. Электрическая индукция. Распределение зарядов в проводниках. Связь между напряженностью поля у поверхности проводников и поверхностной плотностью зарядов.

1) Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии.

2) Электростатическая индукция —перераспределение зарядов в проводнике под действием внешнего эл.стат. поля

4) взаимосвязь между напряженностью Е поля вблизи поверхности заряжен­ного проводника и поверхностной плотностью  зарядов на его поверхности. Для этого применим теорему Гаусса к бесконечно малому цилиндру с основаниями S, пересека­ющему границу проводник — диэлектрик. Ось цилиндра ориентирована вдоль вектора Е. Поток вектора электрического смещения через внутреннюю часть цилинд­рической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Со­гласно теореме Гаусса этот поток (DS) равен сумме зарядов (Q=S), охваты­ваемых поверхностью: DS=S т.е.

Или

где  — диэлектрическая проницаемость среды, окружающей проводник.

8. Электроемкость. Электроемкость уединенного проводника. Электроемкость заряженного шара. Конденсаторы. Соединения конденсаторов.

1)Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. 

2) Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу С=(1Ф)

3)электроемкость шара

4)Конденса́тор – с-ма из 2-х или нескольких проводников разделенных слоем диэлектрика и способных накапливать эл.заряды.

5) Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна _A – _B. Если емкости отдельных конденсаторов С₁, С₂, ..., С_n, то, согласно (94.1), их заряды равны

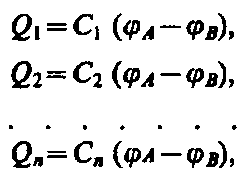
а заряд батареи конденсаторов

Полная емкость батареи

т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдель­ных конденсаторов.

2. Последовательное соединение конденсаторов (рис. 145). У последовательно соеди­ненных конденсаторов заряды всех обкладок равны по модулю, а разность потенци­алов на зажимах батареи

где для любого из рассматриваемых конденсаторов _i = Q/С_i. С другой стороны,

9.Виды конденсаторов. Электроемкость плоского, сферического и цилиндрического конденсатора.

1) Электроемкость плоского2)

3)

10. Энергия системы неподвижных точечных зарядов. Энергия заряженного конденсатора. Энергия электрического поля. Объемная плотность энергии.

1)Электростатические силы взаимодействия консервативны; следовательно, система зарядов обладает потенци­альной энергией. Найдем потенциальную энергию системы двух неподвижных точеч­ных зарядов Q₁иQ₂, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией: где φ₁₂ и φ₂₁ — соответственно потенциалы, создаваемые зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно , поэтому W₁ = W₂ = W и

Добавляя к системе из двух зарядов последовательно зарядыQ₃, Q₄, ... , можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна  где φ_i — потенциал, создаваемый в той точке, где находится заряд Q_i, всеми зарядами, кроме i-го.

2)Энергия заряженного конденсатора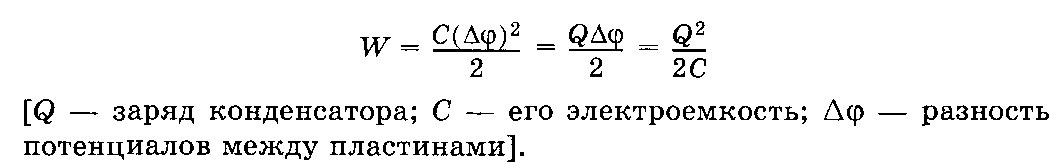

3)Энергия электростатического поля

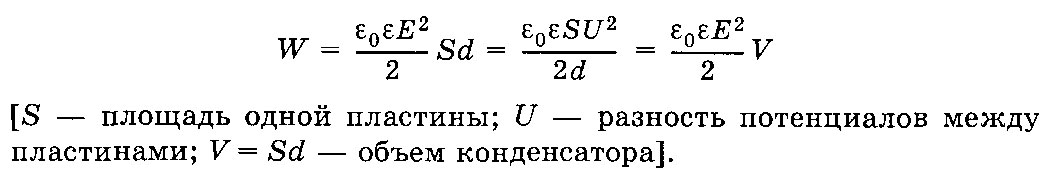
4) Объемная плотность энергии электростатического поля (энергия единицы объема)

11. Электрический ток. Ток проводимости и конвекционный ток. Сила и плотность тока. Условия возникновения и существования электрического тока. ЭДС и напряжение. КПД источников тока. Виды источников тока. Соединение источников тока в батарею.

1)Электри́ческий ток — упорядоченное нескомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля.

2)Ток проводимости – это направленное движение зарядов в проводящих телах: электронов – в металлах, электронов и дырок – в полупроводниках, ионов – в электролитах, ионов и электронов – в газах. Конвекционный ток – это движение заряженных тел и поток электронов или других заряженных частиц в вакууме.

3)Плотность тока – векторная характеристика электрического тока, численно равная отношению силы тока, проходящего сквозь малый элемент поверхности, нормальный к направлению движения заряженных частиц, образующих ток, к площади этого элемента:. j = dl/dS. Количественной мерой электрического тока служит сила тока I скалярная физи­ческая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:

4)Условия возникновения и существования электрического тока

1) наличие свободных носителей зарядов,2) наличие разности потенциалов, 3) замкнутая цепь,4) источник сторонних сил, который поддерживает разность потенциалов.

5)Электродвижущая сила (ЭДС) —— скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

Напряжением U на участке наз-ся физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторон­них сил при перемещении единичного положительного заряда на данном участке цепи.

12. Ток в металлах. Соединение проводников. Единицы сопротивления. Удельное сопротивление и удельная проводимость проводников. Параллельное и последовательное соединение проводников.

1)Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля.

2)Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

3)Единица измерения – Ом.

4)Удельное сопротивление электрическое (r), физическая величина, равная электрическому сопротивлению цилиндрического проводника единичной длины и единичной площади поперечного сечения. Обычно У. с. выражают в ом×см или ом×м.

Удельной проводимостью называют меру способности вещества проводить электрический ток.

13. Зависимость сопротивление проводников от материала, размеров и температуры. Температурный коэффициент сопротивления. Сверхпроводимость. Применение сверхпроводящих металлов.

Сопротивление проводников зависит от его размеров и формы, а также от материала,

1) Сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения: R = ρl/S; ρ - удельное сопротивление проводника.

У металлических проводников сопротивление с увеличением температуры возрастает ρ = ρ˳(1+αt); Здесь ρ˳ - сопротивление при нуле по Цельсию, α - термический коэффициент сопротивления. При очень низких температурах указанная зависимость не выполняется.

2)Температурный коэффициент электрического сопротивления — величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу.

3)Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура).

4)Явление сверхпроводимости используется для получения сильных магнитных полей, поскольку при прохождении по сверхпроводнику сильных токов, создающих сильные магнитные поля, отсутствуют тепловые потери.

14. Закон Ома для участка цепи в интегральной и дифференциальной форме.

Закон Ома в интегральной форме Закон Ома для участка электрической цепи имеет вид: U = RI где: U — напряжение или разность потенциалов,I — сила тока, R — сопротивление Закон Ома также применяется ко всей цепи, но в несколько изменённой форме: I=E/(R+r), где: e — ЭДС цепи, I — сила тока в цепи, R — сопротивление всех элементов цепи, r — внутреннее сопротивление источника питания. Закон Ома в дифференциальной форме Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: j=γ*E, где j- вектор плотности тока, γ — удельная проводимость, E — вектор напряжённости электрического поля.

15. Работа и мощность тока. Единицы работы и мощности. Закон Джоуля-Ленца в интегральной и дифференциальной формах.

Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения, где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.

Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле или P = IU.

Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж. 1 Дж = Кл·В = А·В·с.

Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.

Закон Джоуля-Ленца в интегральной и дифференциальной формах - если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. В любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна в интегральной форме

Используя дифференциальную форму закона Ома (j=Е) и соотношение =1/, получим в диффер. форме

16. Закон Ома для замкнутой электрической цепи. Режим короткого замыкания. Закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме.

Закон Ома для замкнутой электрической цепи

Режим коро́ткого замыка́ния в электротехнике — состояние двухполюсника, при котором его выводы соединены проводником с близким к нулевому сопротивлением.

Закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме.

.

, где представляет собой суммарное сопротивление участка цепи, первый интеграл в правой части - разность потенциалов на концах участка, а второй интеграл определяет ЭДС , действующую на участке цепи. Таким образом , в интегральной форме.

17. Разветвленные цепи. Первое и второе правило Кирхгофа. Применение правил Кирхгофа для расчета электрических цепей.

Разветвленные цепи- цепи, содержащие несколь­ко замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т. д.).

Первое правило (правило узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю (положительными считаются токи, втекающие в узел, отрицательными - токи, отходящие от узла).

Второе правило (правило контуров): в любом замкнутом контуре, произвольно выбранном в электрической цепи, алгебраическая сумма произведений токов на сопротивления соответствующих участков этого контура равна алгебраической сумме э.д.с. в контуре.

Возьмём следующую цепь:

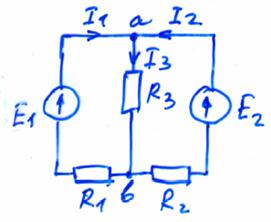
Для составления уравнений двух законов Кирхгофа при расчёте токов в подобной цепи сначала произвольно размечаем направление токов в ней. Затем при составлении уравнений для узлов следует иметь в виду, что число независимых уравнений будет на 1 меньше числа узлов m, т.е. число этих уравнений будет  m – 1.

Для узла а:    - I₁ – I₂ + I₃ = 0

Для узла b:    -I₃ + I₁ + I₂ = 0,

Т.е. второе уравнение содержит те же токи, что и первое уравнение и будет лишним. При составлении уравнений на основании второго закона Кирхгофа надо так выбрать контуры обхода, чтобы в каждый последующий контур входило не менее одной ветви, не включённой в ранее обойдённые контуры. Число ветвей  n  равно числу неизвестных токов. Для определения этих  n  токов уже составлено на основании первого закона Кирхгофа (m – 1) уравнений. Следовательно, для расчёта токов согласно второму закону Кирхгофа нужно составить ещё   n – m + 1  уравнений.

Для нашей схемы, где n = 3, а  m = 2, число уравнений второго закона Кирхгофа будет n – m + 1 = 3 – 2 + 1 =2. Эти уравнения будут:

E₁ = I₁·R₁ + I₃·R₃

E₂ = I₂·R₂ + I₃·R₃

(третий контур в этой цепи содержит ветви, уже вошедшие в первые 2 контура, поэтому уравнение E₁ – E₂ = I₁·R₁ – I₂·R₂ будет для расчётов ненужным).