39. Рангово-бисериальный коэффициент корреляции.

О корреляции вообще см. вопрос № 36 с. 56 (64) 063.JPG

harchenko-korranaliz.pdf с. 28

Рангово-бисериальный коэффициент корреляции, используемый в случаях, когда одна из переменных (Х) представлена в порядковой шкале, а другая (Y) – в дихотомической, вычисляется по формуле

.

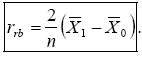
Здесь – средний ранг объектов, имеющих единицу по Y; – средний ранг объектов с нулем по Y, n – объем выборки.

Проверка гипотезы о значимости рангово-бисериального коэффи-циента корреляции осуществляется аналогично точечному биссериальному коэффициенту корреляции с помощью критерия Стьюдента с заменой в формулах rpb на rrb.

http://noleex.ru/0078.htm

В тех случаях, когда одна переменная измеряется в дихотомической шкале (переменная X), а другая в ранговой шкале (переменная У), используется рангово-бисериальный коэффициент корреляции. Мы помним, что переменная X, измеренная в дихотомической шкале, принимает только два значения (кода) 0 и 1. Особо подчеркнем: несмотря на то что этот коэффициент изменяется в диапазоне от –1 до +1, его знак для интерпретации результатов не имеет значения. Это еще одно исключение из общего правила.

Расчет этого коэффициента производится по формуле:

где `X1– средний ранг по тем элементам переменной Y, которым соответствует код (признак) 1 в переменной Х;

`X0– средний ранг по тем элементам переменной Y, которым соответствует код (признак) 0 в переменной Х\

N – общее количество элементов в переменной X.

Для применения рангово-бисериального коэффициента корреляции необходимо соблюдать следующие условия:

1.  Сравниваемые переменные должны быть измерены в разных шкалах: одна X – в дихотомической шкале; другая Y– в ранговой шкале.

2.  Число варьирующих признаков в сравниваемых переменных Xи Y должно быть одинаковым.

3.  Для оценки уровня достоверности рангово-бисериального коэффициента корреляции следует пользоваться формулой (11.9)и таблицей критических значений для критерия Стьюдентапри k = n – 2.

http://psystat.at.ua/publ/drugie_vidy_koehfficienta_korreljacii/1-1-0-38

Случаи, когда одна из переменных представлена в дихотомической шкале, а другая в ранговой (порядковой), требуют применения коэффициента рангово-бисериальной  корреляции: rpb=2 / n * (m1 - m0) где: n – число объектов измерения m1 и m0 - средний ранг объектов с 1 или 0 по второй переменной. Данный коэффициент также применяется при проверке валидности тестов.

40. Коэффициент линейной корреляции.

О корреляции вообще (и в частности о линейной как раз) см. вопрос № 36 с. 56 (64) 063.JPG

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ г-ПИРСОНА

r-Пирсона (Pearson r) применяется для изучения взаимосвязи двух метричес­ких переменных, измеренных на одной и той же выборке. Существует множество ситуаций, в которых уместно его применение. Влияет ли интеллект на успе­ваемость на старших курсах университета? Связан ли размер заработной пла­ты работника с его доброжелательностью к коллегам? Влияет ли настроение школьника на успешность решения сложной арифметической задачи? Для ответа на подобные вопросы исследователь должен измерить два интересую­щих его показателя у каждого члена выборки. Данные для изучения взаимо­связи затем сводятся в таблицу, как в приведенном ниже примере.

ПРИМЕР 6.1

В таблице приведен пример исходных данных измерения двух показателей интел­лекта (вербального и невербального) у 20 учащихся 8-го класса.

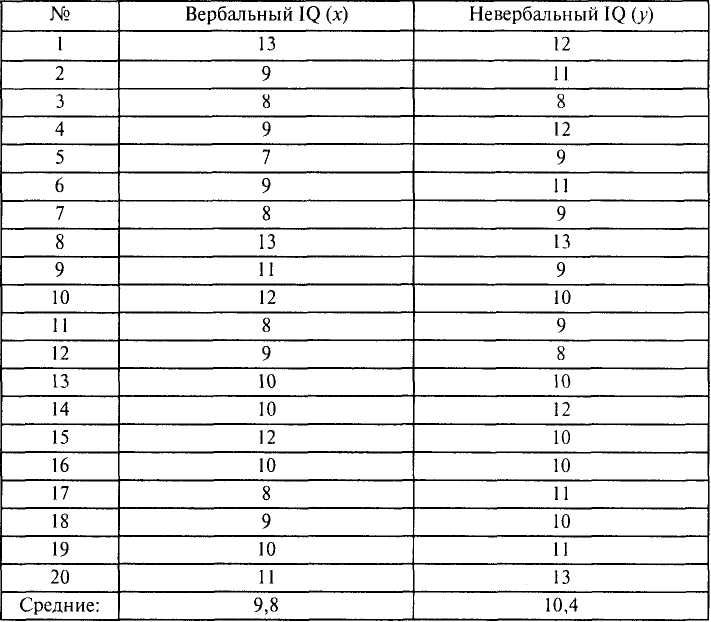
Связь между этими переменными можно изобразить при помощи диаграммы рас­сеивания (см. рис. 6.3). Диаграмма показывает, что существует некоторая взаимо­связь измеренных показателей: чем больше значения вербального интеллекта, тем (преимущественно) больше значения невербального интеллекта.

Прежде чем дать формулу коэффициента корреляции, попробуем просле­дить логику ее возникновения, используя данные примера 6.1. Положение каждой /-точки (испытуемого с номером /) на диаграмме рассеивания отно­сительно остальных точек (рис. 6.3) может быть задано величинами и знака­ми отклонений соответствующих значений переменных от своих средних ве­личин: (xj — MJ и (у, —М_у). Если знаки этих отклонений совпадают, то это свидетельствует в пользу положительной взаимосвязи (большим значениям по х соответствуют большие значения по у или меньшим значениям по х со­ответствуют меньшие значения по у).

Для испытуемого № 1 отклонение от среднего по х и по у положительное, а для испытуемого № 3 и то и другое отклонения отрицательные. Следовательно, данные того и другого свидетельствуют о положительной взаимосвязи изучаемых призна­ков. Напротив, если знаки отклонений от средних по х и по у различаются, то это будет свидетельствовать об отрицательной взаимосвязи между признаками. Так, для испытуемого № 4 отклонение от среднего по х является отрицательным, по у — положительным, а для испытуемого № 9 — наоборот.

Таким образом, если произведение отклонений (х,— М_х) х (у, — М_у) поло­жительное, то данные /-испытуемого свидетельствуют о прямой (положи­тельной) взаимосвязи, а если отрицательное — то об обратной (отрицатель­ной) взаимосвязи. Соответственно, если х w у ъ основном связаны прямо пропорционально, то большинство произведений отклонений будет поло­жительным, а если они связаны обратным соотношением, то большинство произведений будет отрицательным. Следовательно, общим показателем для силы и направления взаимосвязи может служить сумма всех произведений отклонений для данной выборки:

При прямо пропорциональной связи между переменными эта величина является большой и положительной — для большинства испытуемых откло­нения совпадают по знаку (большим значениям одной переменной соответ­ствуют большие значения другой переменной и наоборот). Если же х и у име­ют обратную связь, то для большинства испытуемых большим значениям одной переменной будут соответствовать меньшие значения другой перемен­ной, т. е. знаки произведений будут отрицательными, а сумма произведений в целом будет тоже большой по абсолютной величине, но отрицательной по знаку. Если систематической связи между переменными не будет наблюдать­ся, то положительные слагаемые (произведения отклонений) уравновесятся отрицательными слагаемыми, и сумма всех произведений отклонений будет близка к нулю.

Чтобы сумма произведений не зависела от объема выборки, достаточно ее усреднить. Но мера взаимосвязи нас интересует не как генеральный параметр, а как вычисляемая его оценка — статистика. Поэтому, как и для формулы дис­персии, в этом случае поступим также, делим сумму произведений отклоне­ний не на N, а на TV— 1. Получается мера связи, широко применяемая в физи­ке и технических науках, которая называется ковариацией (Covahance):

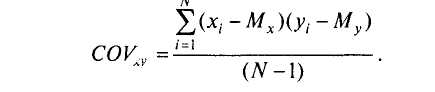
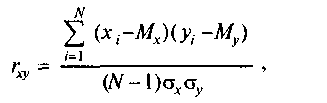В психологии, в отличие от физики, большинство переменных измеряют­ся в произвольных шкалах, так как психологов интересует не абсолютное зна­чение признака, а взаимное расположение испытуемых в группе. К тому же ковариация весьма чувствительна к масштабу шкалы (дисперсии), в которой измерены признаки. Чтобы сделать меру связи независимой от единиц изме­рения того и другого признака, достаточно разделить ковариацию на соот­ветствующие стандартные отклонения. Таким образом и была получена фор­мула коэффициента корреляции К. Пирсона:

(6.1)

или, после подстановки выражений для о_х и

Если значения той и другой переменной были преобразованы в г-значения по формуле

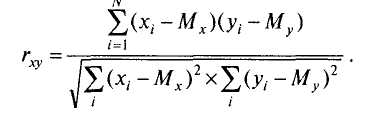
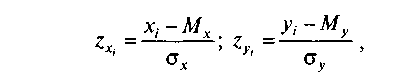
то формула коэффициента корреляции r-Пирсона выглядит проще (071.JPG):

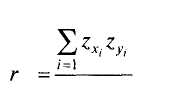
N-l

http://slovari.yandex.ru/dict/sociology/article/soc/soc-0525.htm

КОРРЕЛЯЦИЯ ЛИНЕЙНАЯ - статистическая линейная связь непричинного характера между двумя количественными переменными х и у. Измеряется с помощью "коэффициента К.Л." Пирсона, который является результатом деления ковариации на стандартные отклонения обеих переменных:

,

где s_xy - ковариация между переменными х и у;

s_x, s_y - стандартные отклонения для переменных х и у;

x_i, y_i - значения переменных х и у для объекта с номером i;

x, y - средние арифметические для переменных х и у.

Коэффициент Пирсона r может принимать значения из интервала [-1; +1]. Значение r = 0 означает отсутствие линейной связи между переменными х и у (но не исключает статистической связи нелинейной). Положительные значения коэффициента (r > 0) свидетельствуют о прямой линейной связи; чем ближе его значение к +1, тем сильнее связь статистическая прямая. Отрицательные значения коэффициента (r < 0) свидетельствуют об обратной линейной связи; чем ближе его значение к -1, тем сильнее обратная связь. Значения r = ±1 означают наличие полной линейной связи, прямой или обратной. В случае полной связи все точки с координатами (x_i, y_i) лежат на прямой y = a + bx.

"Коэффициент К.Л." Пирсона применяется также для измерения тесноты связи в модели регрессии линейной парной.