
- •Адгезионный
- •Тепловой
- •Усталостный
- •Фреттинговый
- •20. Материалы и термическая обработка зубчатых колес
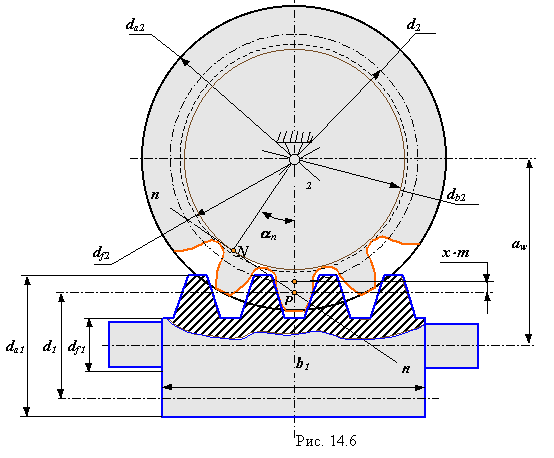
- •23. Расчет на прочность зубчатых цилиндрических эвольвентных передач внешнего зацепления (по гост 21354-87)
- •101. Нагрузочная способность поверхностей зубьев
- •102. Нагрузочная способность зуба при изгибе
- •26. Таблица 17. Геометрические параметры прямозубой конической передачи
- •28. Расчет на контактную прочность
- •31. Расчет геометрии зацепления.
31. Расчет геометрии зацепления.
Исходные данные:
m - модуль осевой; q - коэффициент диаметра червяка; z1 - число витков червяка; aw - межосевое расстояние; x - коэффициент смещения червяка; u - передаточное число.
Параметры инструмента:
h* = (h*w + c*1) - коэффициент высоты витка; h*a - коэффициент высоты головки; s* - коэффициент расчетной толщины; r*f - коэффициент радиуса кривизны переходной кривой;
c*1,2 = 0.25 ... 0.5 ; s* = 0.75 Ч p ; r*f = 0.3 ... 0.45 .
Расчет геометрических параметров.
Число зубьев колеса
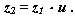
Коэффициент смещения ( если задано межосевое расстояние )
![]()
Межосевое расстояние ( если задан коэффициент смещения )
![]()
Делительные диаметры
![]()
Начальные диаметры
![]()
Делительный угол подъема витка червяка
![]()
Начальный угол подъема витка червяка
![]()
Основной угол подъема витка червяка ( только для червяков ZI )
![]()
и
основной диаметр червяка
![]()
Высота витка червяка
![]()
Высота головки витка червяка
![]()
Диаметры вершин
витков
червяка
![]()
зубьев
червячного колеса в средней торцовой
плоскости
![]()
Диаметры впадин
червяка
![]()
червячного
колеса
![]()
Наибольший диаметр червячного колеса
![]()
Ширина венца червячного колеса
![]()
Длина нарезанной части червяка ( при х= 0 )
![]()
Геометрические показатели качества зацепления.
Подрезание зубьев червячного колеса отсутствует если
![]()
Заострение зубьев в средней торцовой плоскости отсутствует, если
![]()
Заострение зубьев в средней торцовой плоскости отсутствует, если
![]()
3 2.
2.
а) б)
Рис. 38. Шевронная зубчатая передача
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется шевронным (см. рис.1.52, в). Часть венца с зубьями одинакового направления называется полушевроном. Из технологических соображений шевронные колеса изготовляют двух типов (рис.1.60): с дорожкой посередине колеса (а) и без дорожки (б).В шевронном колесе осевые силы Faна полушевронах, направленные в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы, и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах β = 25...40°, в результате чего повышаются прочность зубьев, плавность работы передачи и ее нагрузочная способность. Шевронные колеса применяют в мощных быстроходных закрытых передачах. Недостатком шевронных колес является высокая трудоемкость и себестоимость изготовления. Геометрические, кинематические и прочностные расчеты шевронной и косозубой передач аналогичны.
Нетрудно показать, что если ер – целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что благоприятно для работы передачи, так как нагрузка на зубья в процессе зацепления будет оставаться постоянной, а шум и динамические нагрузки уменьшатся. Суммарная длина контактных линий в этом случае равна
/s=6ea/cosp.
Силу нормального давления Fnв зацеплении косозубых колес можно разложить на три взаимно перпендикулярные составляющие (рис. 7.10,6): окружную силу tv, радиальную силу.Рги осевую силу Fa, равные:
Ft=2T/d; Fr=Fctga/cosp; Fa= F,tg|3,
где Т– передаваемый вращающий момент; a– угол зацепления.
Наличие осевой силы – существенный недостаток косозубых передач. Во избежание больших осевых сил в косозубой передаче угол наклона линии зуба ограничивают значениями р = 8... 20°, несмотря на то, что с увеличением р увеличивается прочность зубьев, плавность работы передачи, ее нагрузочная способность.
Расчет шевронной передачи
Исходные данные:
Мощность на валу шестерни и колеса Р1=7,06 кВт
Р1=6,78 кВт
Вращающий момент на шестерне и колесе Т1=388 Нм
Т2=1964 Нм
Передаточное число U=4,5
Частота вращения шестерни и колеса n1=174 об/мин
n2=38,7 об/мин
Угловая скорость вращения шестерни и колеса ω1=18,2 рад/с
ω3=4 рад/с
Угол наклона зубьев β=45˚
Расположение колес относительно опор симметричное.
Материал
зубчатых колес сталь 45 с термообработкой
– улучшение; для колеса твердость
235…262 НВ2
(248 НВ2ср),
sТ
= 540 Н/мм2,
наибольшая толщина сечения заготовки
![]() ;
для шестерни 269…302 НВ1
(285 НВ1ср),
sТ
= 650 Н/мм2,
при диаметре заготовки шестерни
;
для шестерни 269…302 НВ1
(285 НВ1ср),
sТ
= 650 Н/мм2,
при диаметре заготовки шестерни
![]() .
.
При
этом обеспечивается прирабатываемость
зубьев:
![]() .
.
Интерполированием, т.е. находим промежуточные значения функции по известным ее частным значениям, [1,табл.4.15] находим число циклов напряжений, соответствующее пределу выносливости:
для колеса – NHO2 = 16,2´106,
для шестерни – NHO1 = 22,5´106 .
Рекомендуется NF0 = 4´106 – наработка.
Находим число циклов нагружения зубьев (колеса и шестерни) за весь срок службы:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
где
![]() -
ресурс (срок службы) передачи, примерно
три года при двухсменной работе.
-
ресурс (срок службы) передачи, примерно
три года при двухсменной работе.
Принимаем значения коэффициентов:
KHL = 1, учитывает влияние срока службы и режима нагрузки передачи,
KFL = 1, учитывает долговечность работы.
Определяем допускаемые контактные напряжения [s]HO и напряжения изгиба [s]FO, соответствующие числу циклов напряжений NHO и NFO [3, табл. 4.6] для материалов зубьев колеса и шестерни:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Определяем допускаемые напряжения с учетом ресурса (срока службы) передачи:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Чтобы
рассчитать межосевое расстояние,
принимаем расчетные коэффициенты:
![]() –
коэффициент ширины венца [1,табл. 4.6],
–
коэффициент ширины венца [1,табл. 4.6],
![]() ,
,
![]() –
коэффициент неравномерности нагрузки
по длине зуба (табл. 4.18; 4.20).
–
коэффициент неравномерности нагрузки
по длине зуба (табл. 4.18; 4.20).
Тогда межосевое расстояние передачи равно:
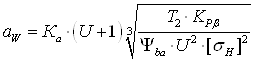
где Ка =43 – числовой коэффициент для шевронной передачи;
Т2=232Нм.
Подставив значения в формулу (5.1) получим:
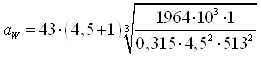 ;
;
![]() мм;
мм;
Принимаем окончательно по ГОСТ2185-66 [1,c.36]
![]() мм.
мм.
Определяем модуль [1,c.36]:
![]()
![]() ;
;
![]() ;
;
Принимаем по ГОСТ9563-60 модуль mn=4,0мм [1,c.36]
Определяем суммарное число зубьев по формуле:
![]()
β=45º, тогда cosβ=0,707
![]() ;
;
![]() ;
;
Принимаем
![]() зуба.
зуба.
Определяем число зубьев шестерни и колеса по формулам [1,c.37]:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Уточняем фактическое передаточное число
![]() ;
;
![]() ;
;
![]()
Отклонения передаточного числа от номинального нет.
Определяем делительные диаметры шестерни и колеса по формуле (3.11):
![]()
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм.
мм.
Проверяем межосевое расстояние
![]()
![]() ;
мм.
;
мм.
Определяем остальные геометрические параметры шестерни и колеса по формулам (2.10)
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() мм;
мм;
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм;
принимаем b2=80мм;
мм;
принимаем b2=80мм;
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм
мм
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм;
мм;
![]() ;
;
![]() мм.
мм.
Проверяем соблюдение условия (т.к. Ψba<0,4)
![]() ;
;
![]() ;
;
![]() ;
;
0,315>0,056
Значит, условие выполняется.
Определяем окружные скорости колес
![]()
![]() ;
;
![]() м/с;
м/с;
![]() ;
;
![]() ;
;
![]() м/с;
м/с;
Принимаем
для расчетов
![]() м/с.
м/с.
Определяем силы в зацеплении
- окружная
![]() ;
;
![]() ;
;
![]() Н;
Н;
- радиальная
![]() ;
;
![]() ;
;
![]() Н;
Н;
- осевого усилия нет.
Принимаем 9-ую степень точности изготовления колес [1,табл.4.5].
Принимаем коэффициенты динамической нагрузки: KHV=1,2 (Н≤350HB); КFV=1,02 [1,табл. 4.13]. Принимаем коэффициенты формы зуба некорригированного зацепления: для шестерни z1 = 16, YF1 = 4,4; а для колеса z2 = 72, YF2 = 3,61. Проверяем зубья колеса по контактным напряжениям и по напряжениям изгиба:
Расчетное контактное напряжение:
;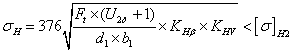
![]() ;
;
Определяем ∆σН
![]() ;
;
![]() ;
;
![]() недогрузки,
что допускается.
недогрузки,
что допускается.
Расчетные напряжения изгиба в основании ножки зубьев колеса и шестерни:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Прочность зубьев на изгиб обеспечивается
Все вычисленные параметры заносим в табл.3.
Параметры закрытой шевронной передачи Таблица 3
Параметр |
Шестерня |
Колесо |
mn,мм |
4 |
|
z |
16 |
72 |
βº |
45º |
|
ha,мм |
4 |
|
hf,мм |
5 |
|
h,мм |
10 |
|
с, мм |
0,5 |
|
d,мм |
90,5 |
409,5 |
dа,мм |
98,5 |
422,5 |
df,мм |
80,5 |
399,6 |
b, мм |
80 |
62 |
ω, рад |
18,2 |
4 |
аW,мм |
250 |
|
v, м/с |
0,8 |
|
Т, Нм |
388 |
1964 |
Ft, Н |
9593 |
|
Fr, Н |
4938 |
|
33. Планетарная передача (дифференциальная передача) — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую (коронную) шестерню, имеющую внутреннее зацепление с планетарными шестернями. Планетарные зубчатые передачи — такие, в которых имеются зубчатые колеса с перемещающимися геометрическими осями. Простейшая планетарная передача (рис. 7.3, а) состоит из вращающегося центрального (солнечного) колеса 1 с наружным зацеплением, неподвижного центрального колеса 3 с внутренним зацеплением и водила Н, на котором закреплены оси сателлитов 2 (3—6 штук). Колеса 1 и 3 называют центральными. Сателлиты совершают планетарное движение, т. е. вращаются вокруг своих осей и вокруг колеса 7. При неподвижном колесе 3 движение может передаваться от колеса 1 к водилу Н и наоборот. При неподвижном водиле получается простая зубчатая передача. Если в планетарной передаче подвижны оба центральных колеса и водило, то такую передачу называют дифференциальной. Передаточное число планетарных передач удобнее всего определять методом остановки водила. По этому методу всем звеньям передачи условно сообщается дополнительное вращение с угловой скоростью водила, но обратной по знаку. Тогда получают так называемый приведенный механизм с неподвижным водилом, представляющий собой простую зубчатую передачу. При определении передаточного числа принимают знак «плюс», если все звенья передачи вращаются в одну сторону, и знак «минус»— если в разные стороны.Основными достоинствами планетарных передач являются возможность осуществления значительных передаточных чисел, компактность, небольшая масса и пр.Однако планетарные передачи требуют повышенной точности изготовления и сложны в сборке. К. п. д. их резко падает с повышением передаточного числа. Планетарные передачи применяют в автомобилях, металлорежущих станках, приборах и т. п.
Дифференциальная пара состоит из двух линий передачи. Каждая линия может представляет собой, например, обычную полосковую или микрополосковую линию передачи, рассмотренную в предыдущих главах книги. Расположенные в непосредственной близости друг от друга, две линии образуют дифференциальную пару. В принципе, из любых двух линий передачи можно образовать дифференциальную пару. Подобно тому, как существует ряд конфигураций поперечных сечений для одиночных линий передач, так же есть разновидности поперечных сечений и для дифференциальных пар линий передач. На рис. 6.4 представлены наиболее распространенные виды поперечных сечений дифференциальных пар, реализуемых на печатных платах.

Рис. 6.4. Наиболее распространенные виды поперечных сечений дифференциальных пар: I — компланарная; 2 — микрополосковая, 3 — полосковая; 4 — развернутосвязанная полосковая.
Хотя, в общем случае, любые две линии передачи могут образовать дифференциальную пару, существует пять особенностей, которые важны при передаче широкополосных сигналов.
1. Наиболее важная особенность дифференциальной пары состоит в том, что она должна иметь однородное поперечное сечение по всей длине и обеспечивать постоянное волновое сопротивление для разных сигналов. Это гарантирует минимальные отражения и искажения сигнала.
2. Вторым важным свойством является то, что временная задержка линии должна быть согласована так, чтобы фронт и спад сигналов в отдельных линиях были точно и четко определены. Любое различие во временной задержке между двумя линиями или иное рассогласование между ними приведут к тому, что дифференциальный сигнал будет преобразован в сигнал общего вида.
3. Обе линии передачи должны быть конструктивно полностью идентичны. Ширина сигнальных проводников и толщина диэлектрического слоя между двумя линиями должны быть одинаковы. Эта свойство называется симметрией. Не должно быть никаких асимметрий, вроде наличия контактной площадки для тестирования или сужений только на одной линии и т. п. Любая асимметрия преобразует дифференциальные сигналы в сигнал общего вида.
35. Червя́чная переда́ча (зубчато-винтовая передача) — механическая передача, Червяки различают по следующим признакам:
по форме поверхности, на которой образуется резьба
цилиндрические
глобоидные
по направлению линии витка
правые
левые
по числу заходов резьбы
однозаходные
многозаходные
по форме винтовой поверхности резьбы
с архимедовым профилем
с конволютным профилем
с эвольвентным профилем
Зубчатые колёса различают по следующим признакам:
по профилю зуба
прямой — (контакт по точке, не нагруженные передачи)
вогнутый — «охватывающий» червяк (контакт по линии)
роликовый — зубы вырожденного сектора заменены на винтовой ролик
по типу зубчатого колеса
полное колесо (полный оборот, непрерывное вращение)
зубчатый сектор (поворот сектора от одного крайнего положения до другого)
вырожденный сектор (в паре с глобоидным червяком — рабочая длина сектора меньше рабочей длины червяка)
осуществляющаяся зацеплением червяка и сопряжённого с ним червячного колеса[1].
36. . Червячные, в которых крутящий момент передается червяком на червячное колесо. Червячные передачи, в свою очередь, подразделяются на передачи с нижним и верхним расположением червяка. Червячные главные передачи иногда применяются в многоосных транспортных средствах с проходной главной передачей (или с несколькими проходными главными передачами) и в автомобильных вспомогательных лебедках.
В червячных передачах ведомое шестеренчатое колесо имеет однотипное устройство (всегда большого диаметра, который зависит от заложенного в конструкцию редуктора передаточного отношения, всегда выполняется с косыми зубьями). А червяк может иметь различную конструкцию. По форме червяки разделяются на цилиндрические и глобоидные. По направлении линии витка - на левые и правые. По числу канавок резьбы - на однозаходные и многозаходные. По форме резьбовой канавки - на червяки с архимедовым профилем, с конволютным профилем и эвольвентным профилем.
2. Цилиндрические главные передачи, в которых крутящий момент передается парой цилиндрических шестерен - косозубых, прямозубых или шевронных. Цилиндрические главные передачи устанавливаются в переднеприводные автомобили с поперечно расположенным двигателем.
3. Гипоидные (или спироидные) главные передачи, в которых крутящий момент передается парой шестерен с косыми или криволинейными зубьями. Пара шестерен гипоидной передачи либо соосна (встречается реже), либо оси шестерен смещены относительно друг друга - с нижним или верхним смещением. За счет сложной формы зубьев площадь зацепления увеличена, и шестеренчатая пара способна передавать больший крутящий момент, чем шестерни главной передачи других типов. Гипоидные передачи устанавливаются в легковые и грузовые автомобили классической (заднеприводной с передним расположением двигателя) и заднемоторной компоновок.
37. Силы в червячном зацеплении определяют для случая контакта рабочих поверхностей в полюсе зацепления и раскладывают по трем взаимно перпендикулярным осям.
Окружная сила на колесе равна по модулю осевой силе на червяке:
![]()
Окружная сила на червяке равна осевой силе на колесе:
![]()
Радиальная сила, раздвигающая червяк и колесо:
![]()
В этих зависимостях T2 и T1 – вращающие моменты на валах колеса и червяка, α – угол профиля витка червяка, d2 – делительный диаметр колеса, dw1 – начальный диаметр червяка.
38. Тепловой расчет червячной передачи
В червячной передаче имеют место сравнительно большие потери передаваемой мощности на трение, передача работает с большим тепловыделением.
Если отвод тепла будет недостаточен, передача перегреется. Так как смазочные свойства масла при нагреве резко ухудшаются, то возникает опасность заедания передачи и выхода ее из строя. При установившемся режиме работы червячного редуктора количество тепла, выделяемого в нем, равно количеству отводимого от него тепла. Этот тепловой баланс устанавливается при определенном перепаде температур между находящимся в редукторе маслом и окружающим корпус воздухом. Тепловой режим работы редуктора нормальный, если перепад температур находится в допустимых пределах. Для обеспечения нормальной работоспособности для червячных редукторов (закрытой передачи) производят тепловой расчет. Тепловой расчет червячной передачи при установившемся режиме работы производят на основе теплового баланса, т. е. приравнивания тепловыделения теплоотводу.
Условие нормального теплового режима:
![]() (13)
(13)
где
![]() —
температура
масла в корпусе редуктора;
—
температура
масла в корпусе редуктора;
![]() — допускаемая температура масла в
корпусе редуктора. Допускаемое значение
зависит
от сорта масла, его способности сохранять
смазывающие свойства при повышении
температуры. Для обычных редукторных
масел допускают t1=
60...70°С,
в исключительных случаях
=
90 °С;
-
определяют из условия теплового баланса,
а именно:
выделяемое червячной парой тепло должно
полностью отводиться в окружающую среду
— допускаемая температура масла в
корпусе редуктора. Допускаемое значение
зависит
от сорта масла, его способности сохранять
смазывающие свойства при повышении
температуры. Для обычных редукторных
масел допускают t1=
60...70°С,
в исключительных случаях
=
90 °С;
-
определяют из условия теплового баланса,
а именно:
выделяемое червячной парой тепло должно
полностью отводиться в окружающую среду
![]()
![]() —
количество
теплоты, выделяемое передачей при
непрерывной работе;
—
количество
теплоты, выделяемое передачей при
непрерывной работе;
![]() — количество теплоты, отводимое свободной
поверхностью корпуса передачи за то
же время.
— количество теплоты, отводимое свободной
поверхностью корпуса передачи за то
же время.
Количество теплоты, выделяющейся в передаче в секунду, или тепловая мощность
![]()
где
P1
– мощность на входном валу передаваемая
червяком, Вт;
![]() – КПД передачи
– КПД передачи
Количество тепла, отводимое через поверхность охлаждения корпуса редуктора,
![]()
где
А
–
площадь поверхности корпуса передачи,
соприкасающаяся с воздухом, м2.
В площадь поверхности охлаждения
А
входит площадь наружной поверхности
корпуса редуктора без днища. Если корпус
снабжен охлаждающими ребрами, то
учитывают только 50% площади их поверхности.;
–
внутренняя температура редуктора или
температура масла, °С;
![]() –
температура окружающей среды (воздуха),
°С (при проектировании обычно принимают
=
20°С);
–
температура окружающей среды (воздуха),
°С (при проектировании обычно принимают
=
20°С);
![]() –
коэффициент
теплопередачи — количество теплоты,
передаваемое в окружающую среду с
единицы поверхности в 1
с
при разности.
температур
в 1°С,
Вт/(м2
°С). При нормальной циркуляции воздуха
вокруг корпуса
=
(14-17,5) Вт/(м2
0С),
при плохой –
=
(8-10,5)
Вт/(м2
°С).
–
коэффициент
теплопередачи — количество теплоты,
передаваемое в окружающую среду с
единицы поверхности в 1
с
при разности.
температур
в 1°С,
Вт/(м2
°С). При нормальной циркуляции воздуха
вокруг корпуса
=
(14-17,5) Вт/(м2
0С),
при плохой –
=
(8-10,5)
Вт/(м2
°С).
Итак, на основании теплового баланса можно определить температуру масла
![]() (14)
(14)
Тепловой расчет червячной передачи выполняют как проверочный.
При
![]() необходимо предпринять меры от перегрева.
необходимо предпринять меры от перегрева.
