Метод Ньютона — Рафсона

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.

48. Классификация задач на условный экстремум. Особенности решения задач на условный экстремум, возможные варианты положения экстремума в задаче математического программирования. Решение классической задачи на условный экстремум методом множителей Лагранжа.

Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно ограничений , меняется от единицы до .

Составим функцию Лагранжа в виде линейной комбинации функции f и функций , взятых с коэффициентами, называемыми множителями Лагранжа — λ_i:

где .

Составим систему из n + m уравнений, приравняв к нулю частные производные функции Лагранжа по x_j и λ_i.

Если полученная система имеет решение относительно параметров x'_j и λ'_i, тогда точка x' может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

49. Распространение метода множителей Лагранжа на задачу математического программирования. Активные и неактивные ограничения. Условия Куна-Такера в задаче математического программирования.

50. Задачи выпуклого программирования. Понятие выпуклой области, выпуклой (вогнутой) функции. Применение условий Куна-Такера при решении задачи выпуклого программирования.

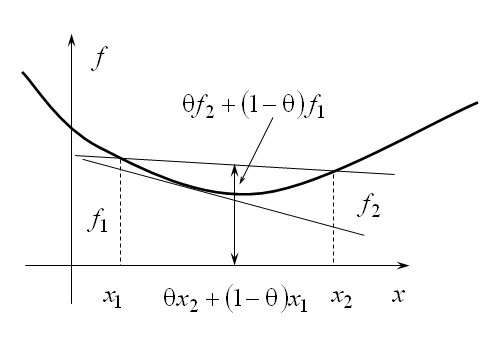
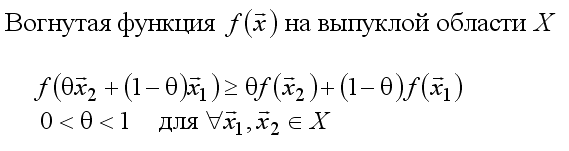
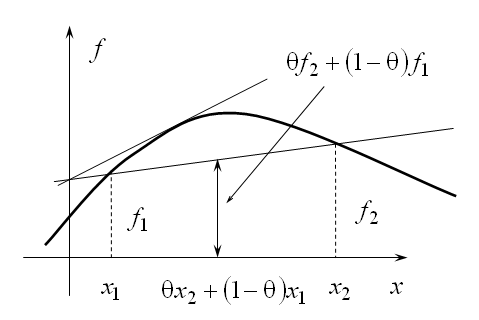
51. Численный методы решения задач условной оптимизации – комплексный метод Бокса.

52. Последовательная оптимизация без ограничений – метод штрафной функции. Численный алгоритм реализации метода штрафной функции - метод Кэрролла-Фиакко-Маккормика.