44. Задача многомерной безусловной оптимизации. Градиентные методы:

Основная идея методов заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом  :

где λ^[j] выбирается

• постоянной, в этом случае метод может расходиться;

• дробным шагом, то есть длина шага в процессе спуска делится на некое число;

• наискорейшим спуском: 

Метод наискорейшего спуска (метод градиента)

Выбирают  , где все производные вычисляются при  , и уменьшают длину шага λ^[j] по мере приближения к минимуму функции F.

Для аналитических функций F и малых значений f_i тейлоровское разложение F(λ^[j]) позволяет выбрать оптимальную величину шага

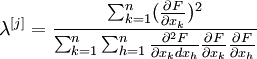(5)

где все производные вычисляются при  .

Алгоритм

1. Задаются начальное приближение и точность расчёта 

2. Рассчитывают  , где 

3. Проверяют условие останова:

   • Если  , то j = j + 1 и переход к шагу 2.

   • Иначе   и останов.

45. Задача многомерной безусловной оптимизации. Метод Флетчера-Ривса (сопряженных градиентов). Метод оврагов.

Метод оврагов

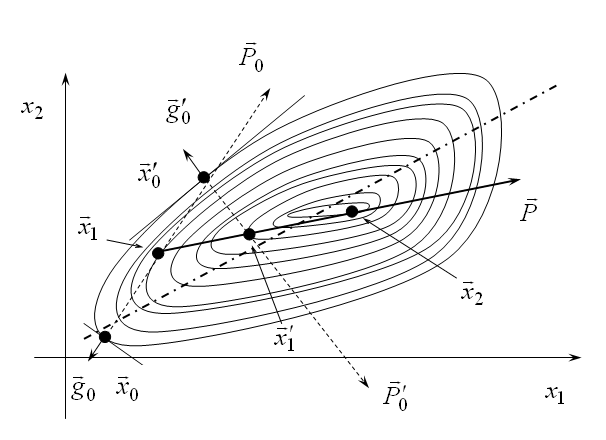
Метод Флетчера-Ривса.

Позволяет найти минимум не линейной целевой функции многих переменных вида

M=F(x1 , x2, . . ., xN)

при отсутствии ограничений. Метод основан на применении частных

производных целевой функции по независимым переменным и предназначен для

исследования унимодальных функций. С его помощью можно исследовать и

мультимодальные функции, однако в этом случае следует брать несколько

исходных точек и проверять, одинаково ли во всех случаях решение

46. Задача многомерной безусловной оптимизации. Семейство методов с переменной метрикой: основная идея всех методов, общий цикл вычислений, метод Давидона-Флетчера-Пауэлла, метод Гольдфарба.

й

47. Задача многомерной безусловной оптимизации. Методы II порядка: Ньютона и Ньютона-Рафсона. Сравнение методов решения задачи многомерной безусловной оптимизации.

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции

Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства. Пусть необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:

где  — гессиан функции .

В более удобном итеративном виде это выражение выглядит так:

Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.