
- •36. Задача нелинейной безусловной оптимизации (одномерная, многомерная). Классический метод решения – условия оптимальности.
- •38. Задача одномерной безусловной оптимизации. Метод деления отрезка пополам (дихотомии). Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.
- •39. Задача одномерной безусловной оптимизации. Метод золотого сечения. Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.
- •40. Задача одномерной безусловной оптимизации. Метод чисел Фибоначчи. Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.
- •41. Задача одномерной безусловной оптимизации. Методы спуска к минимуму из некоторой начальной точки: метод последовательного перебора, метод квадратичной параболы, метод кубической параболы.
- •42. Задача многомерной безусловной оптимизации. Классификация численных методов поиска решения. Покоординатные методы: общий подход, метод Гаусса-Зейделя, метод Розенброка, метод Пауэлла.
- •43. Задача многомерной безусловной оптимизации. Симплексный метод Нельдера-Мида.
- •Алгоритм
- •44. Задача многомерной безусловной оптимизации. Градиентные методы:
- •Метод наискорейшего спуска (метод градиента)
- •Алгоритм
- •45. Задача многомерной безусловной оптимизации. Метод Флетчера-Ривса (сопряженных градиентов). Метод оврагов.
- •46. Задача многомерной безусловной оптимизации. Семейство методов с переменной метрикой: основная идея всех методов, общий цикл вычислений, метод Давидона-Флетчера-Пауэлла, метод Гольдфарба.
- •47. Задача многомерной безусловной оптимизации. Методы II порядка: Ньютона и Ньютона-Рафсона. Сравнение методов решения задачи многомерной безусловной оптимизации.
- •Метод Ньютона — Рафсона
36. Задача нелинейной безусловной оптимизации (одномерная, многомерная). Классический метод решения – условия оптимальности.




37. Задача одномерной безусловной оптимизации. Общая схема интервальных методов одномерного поиска. Унимодальные функции, интервал неопределённости (локализации) минимума, уменьшение интервала неопределённости – пассивный и последовательный поиск. Понятие оптимального поиска.




38. Задача одномерной безусловной оптимизации. Метод деления отрезка пополам (дихотомии). Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.
В данном разделе рассматривается метод дихотомического поиска и метод золотого сечения. В обоих методах на интервале а<х<Ь ищется максимум функции f(x), имеющей на этом интервале только один максимум. (Такая функция называется одновершинной.) Начальный интервал неопределенности состоит из исходного интервала I[0] = (а, Ь).
Пусть I[i-1] =(xL, xR) — интервал неопределенности на шаге i (на нулевом шаге
X[L] = а и x[R] = b). Далее определяем x1 и х2 такие, что
хL<х1<х2<х[R].
Следующий интервал неопределенности I[i] определяется после вычисления значений f(x1) и f(x2). При этом возможны три варианта.
1. Если f(x1) > f(x2), то точка экстремума х* должна лежать между x[L] и х2:
Х[L] < х* < х2. Тогда положим x[R] = х2 и получим новый интервал неопределенности I[i] = (x[L], x2)(рис. а).
2. Если f(x1) < f(x2), то x1< x* < x[R]. Тогда x[L] = х1 и I[i] = (x1, х[R]) (см. рис. 21.1, б).
3. Если f(x1) = f(x2), то х1 < х* < х2 Положим x[L] = x1 и x[R] = х2, тогда I[i] = (х1, х2).




![]()

39. Задача одномерной безусловной оптимизации. Метод золотого сечения. Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.
Пред вопрос до формул x1 и x2




40. Задача одномерной безусловной оптимизации. Метод чисел Фибоначчи. Величина интервала неопределенности после вычисления значения целевой функции в n промежуточных точках.



41. Задача одномерной безусловной оптимизации. Методы спуска к минимуму из некоторой начальной точки: метод последовательного перебора, метод квадратичной параболы, метод кубической параболы.
Метод перебора (метод равномерного поиска) — простейший из методов поиска значений действительно-значных функций по какому-либо из критериев сравнения (на максимум, на минимум, на определённую константу).
Проиллюстрируем суть метода равномерного поиска посредством рассмотрения задачи нахождения минимума.
Пусть
задана функция ![]() .
И задача
оптимизации выглядит
так:
.
И задача
оптимизации выглядит
так: ![]() Пусть
также задано число наблюдений n.
Пусть
также задано число наблюдений n.
Тогда отрезок ![]() разбивают
на
разбивают
на ![]() равных
частей точками деления:
равных
частей точками деления:
![]()
Вычислив
значения ![]() в
точках
в
точках ![]() ,
найдем путем сравнения точку
,
найдем путем сравнения точку ![]() ,
где
,
где ![]() —
это число от
—
это число от ![]() до
до ![]() такую,
что
такую,
что
![]() для
всех
для
всех ![]() от
до
.
от
до
.
Тогда интервал
неопределённости составляет
величину ![]() ,
а погрешность определения
точки минимума
функции
соответственно
составляет :
,
а погрешность определения
точки минимума
функции
соответственно
составляет :![]() .
.
Модификация
Если заданное количество измерений чётно (n = 2k), то разбиение можно проводить другим, более изощрённым способом:
![]()
![]() ,
где δ — некая константа из
интервала
,
где δ — некая константа из
интервала  .
.
Тогда
в худшем случае интервал
неопределённости имеет
длину ![]() .
.
Метод квадратичной параболы


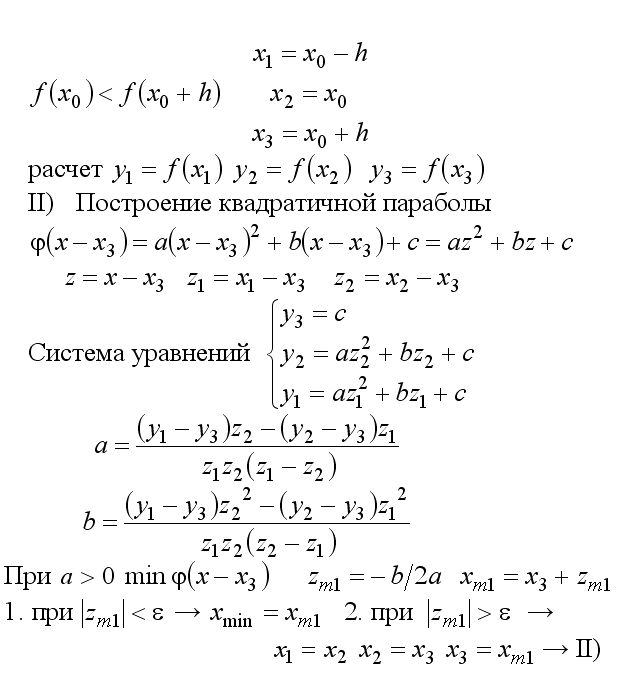
Метод кубич параболы



