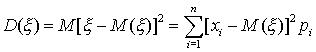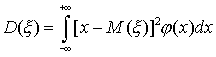8.1.2. Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку  :

Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2.   —неубывающая функция, т.е.

, если 

Доказательство. Пусть  . Событие, состоящее в том, что   примет значение, меньшее  , можно подразделить на следующие два несовместных события: 1)   примет значение, меньшее  , с вероятностью  ; 2)   примет значение, удовлетворяющее неравенству  , с вероятностью  .

По теореме сложения имеем

Отсюда

или

(8.1)

Так как любая вероятность есть число неотрицательное, то  , или , что и требовалось доказать.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале  , равна приращению функции распределения на этом интервале:

(8.2)

Это важное следствие вытекает из формулы (8.1), если положить   и  .

Пример 8.1. Случайная величина   задана функцией распределения

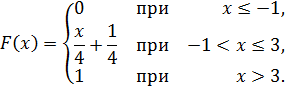
Найти вероятность того, что в результате испытания   примет значение, принадлежащее интервалу 

Решение. Так как на интервале  , по условию,

то

Итак,

Следствие 2. Вероятность того, что непрерывная случайная величина   примет одно определенное значение, равна нулю.

Действительно, положив в формуле (8.2)    , имеем

Устремим   к нулю. Так как   — непрерывная случайная величина, то функция   непрерывна. В силу непрерывности   в точке   разность   также стремится к нулю; следовательно,   Используя это положение, легко убедиться в справедливости равенств

(8.3)

Например, равенство   доказывается так:

Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство нулю вероятности   означает, что событие   невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений; в частности, это значение может оказаться равным  .

Свойство 3. Если возможные значения случайной величины принадлежат интервалу  , то: 1)   при  ; 2)   при  .

Доказательство.

1) Пусть  . Тогда событие   невозможно (так как значений, меньших   величина   по условию не принимает) и, следовательно, вероятность его равна нулю.

2) Пусть  . Тогда событие   достоверно (так как все возможные значения   меньше  ) и, следовательно, вероятность его равна единице.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси  , то справедливы следующие предельные соотношения:

Билет 27

Плотность распределения и её свойства.

Определение 3. Производная от функции распределения не­прерывной случайной величины Х называется плотностью рас­пределения вероятностей X:

Из этого определения следует, что функция распределения является первообразной для плотности распределения или не­определенным интегралом от нее. Плотность распределения — это "скорость" изменения вероятности Р(Х < х). Из свойства 2 функции распределения следует справедливость следующей фундаментальной теоремы.

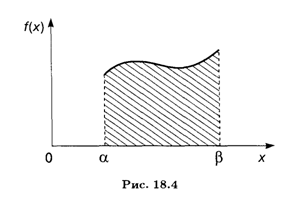
ТЕОРЕМА 5. Вероятность того, что непрерывная случай­ная величина Х примет значение на интервале [α, β), опре­деляется по формуле

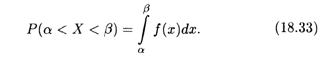
Вспоминая геометрический смысл определенного интеграла (см. п. 7.5), можно сказать, что вероятность того, что непрерывная случайная величина Х примет значение, при­надлежащее интервалу (α, β), равна площади криволинейной трапеции, ограниченной сверху кривой плотности распределе­ния F(X), снизу — осью Ох, а с краев — вертикальными пря­мыми Х = α и Х = β (рис. 18.4).

Связь между функцией распределения и плотностью рас­пределения вероятностей устанавливается, согласно (18.32), формулой

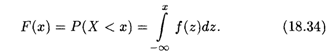
Билет 28

22Математическое ожидание случайной величины.

Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины.

Для вычисления математического ожидания для ДСВ каждое значение x_iучитывается с «весом», пропорциональным вероятности этого значения.

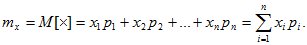(6.1)

M[X]-оператор математического ожидания;

m_x -- число, полученное после вычислений по формуле.

Для НСВ заменим отдельные значения   непрерывно изменяющимся параметром  , соответствующие вероятности  - элементом вероятности  , а конечную сумму – интегралом: 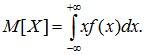 (6.2)

Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами  , в которых сосредоточены соответственно массы р₁, р₂,...., причем  . Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью  .

Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.

, (6.3)

где сумма распространяется на все значения x_i, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.

Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.

Свойства математического ожидания.

1. Математическое ожидание неслучайной величины с равно самой величине с:

M[c] = c. (6.4)

Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1:

M[c]=c∙1=c.

2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание:

M[c×X] = c×M[X]. (6.5)

Доказательство:

3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:

(6.6)

Доказательство: следует из свойств 1 и 3.

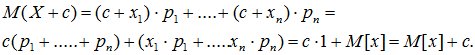
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

M[X+Y] = M[X]+M[Y]. (6.6)

Билет 29

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.     2. Дисперсия и ее свойства. Среднее квадратическое отклонение.     Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения   случайной величины от ее математического ожидания.     Предварительно рассмотрим пример. Пусть две случайные величины   и   заданы следующими рядами распределения  

Значения	-0,2	-0,1	0,1	0,2
Вероятности p(x)	0,25	0,25	0,25	0,25

 

Значения	-50	-40	40	50
Вероятности p(x)	0,25	0,25	0,25	0,25

   Легко убедится в том, что математические ожидания этих величин одинаковы и равны нулю:  

   Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной  , близки к ее математическому ожиданию, а во втором случае далеки от него. Для оценки разброса (рассеяния) значений случайной величины около ее математического ожидания вводится новая числовая характеристика - дисперсия.     Дисперсией   случайной величины   называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

(43)

   Пусть   - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина   принимает значения

с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

(44)

   Если же   - случайная величина с плотностью распределения  , то по определению

(45)

   Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

   Так как   и   - постоянные, то используя свойства математического ожидания, получим

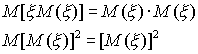
   Следовательно,

   Откуда окончательно находим

(46)

   Рассмотрим теперь свойства дисперсии.     1°. Дисперсия постоянной равна нулю. (Доказательство)     2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(47)

(Доказательство)

   3°. Если   и   - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

(48)

(Доказательство)

   Средним квадратическим отклонением   случайной величины   называется корень квадратный из ее дисперсии:

(49)

   Среднее квадратическое отклонение   имеет ту же размерность, что и случайная величина  . 

Билет 30