Независимые испытания

В вероятностных моделях процедур принятия решений с помощью понятия независимости событий можно придать точный смысл понятию «независимые испытания». Для этого рассмотрим сложный опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события   и  , из которых   определяется по исходу первого испытания, а   — по исходу второго, являются независимыми.

Пример 4. Опишем вероятностное пространство, соответствующее бросанию двух монет независимо друг от друга.

Разбор примера. Пространство элементарных событий состоит из четырёх элементов:   (запись  означает, что первая монета выпала орлом и вторая — тоже орлом; запись   — первая — решкой, а вторая — орлом, и так далее). Поскольку события «первая монета выпала решкой» и «вторая монета выпала орлом» являются независимыми по определению независимых испытаний и вероятность каждого из них равна  , то вероятность   равна  . Аналогично, вероятность каждого из остальных элементарных событий также равна  .

Пример 5. Опишем вероятностное пространство, соответствующее проверке качества двух единиц продукции независимо друг от друга, если вероятность дефектности равна х.

Разбор примера. Пространство элементарных событий состоит из четырёх элементов:

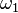•  — обе единицы продукции годны;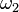

•  — первая единица продукции годна, а вторая — дефектна;

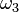•  — первая единица продукции дефектна, а вторая — годна;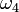

•  — обе единицы продукции являются дефектными.

Вероятность того, что единица продукции дефектна, есть  , а потому вероятность того, что имеет место противоположное событие, то есть единица продукции годна, есть  . Поскольку результат проверки первой единицы продукции не зависит от такового для второй, то

,

,

.

Билет 20

Формула полной вероятности

Предположим, что событие   может осуществиться с одним и только с одним из   попарно несовместных событий  . Тогда

,

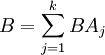где события   и   с разными индексами   и   несовместны. По теореме сложения вероятностей

.

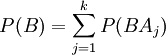Воспользовавшись теоремой умножения, находим, что

.

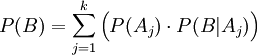Получена так называемая формула полной вероятности. Она широко использовалась математиками при конкретных расчётах ещё в начале XVIII века, но впервые была сформулирована как одно из основных утверждений теории вероятностей Пьером-Симоном Лапласом лишь в конце того века. Она применяется, в частности, при нахождении среднего выходного уровня дефектности в задачах статистического обеспечения качества продукции.

Формулы Байеса

Применим формулу полной вероятности для вывода так называемых формул Байеса, которые иногда используют при проверке статистических гипотез. Требуется найти вероятность события  , если известно, что событие   произошло. Согласно теореме умножения,

.

Следовательно

.

Используя формулу полной вероятности для знаменателя, находим, что

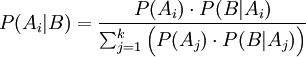Две последние формулы и называют обычно формулами Байеса. Общая схема их использования такова. Пусть событие  может протекать в различных условиях, относительно которых может быть сделано   гипотез  . Априорныевероятности этих гипотез суть  . Известно также, что при справедливости гипотезы  вероятность   равна  . Произведён опыт, в которым произошло  . Естественно после этого уточнить оценки вероятностей гипотез. Апостериорные оценки вероятностей гипотез   даются формулами Байеса. В прикладной статистике существует направление байесовская статистика, в которой, в частности, на основе априорного распределения параметров после проведения измерений, наблюдений, испытаний, опытов анализов вычисляют уточнённые оценки параметров.

Билет 21

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведенииn испытаний событие A появится ровно k раз.

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Билет 22

Предельные теоремы для схемы Бернулли

Так как ν_n число успехов в последовательности из n независимых испытаний Бернулли, можно представить в виде:

 (1)

где   - независимые одинаково распределенные бернуллиевские случайные величины. Мы знаем в явном виде распределение ν_n, а именно:  , где p - вероятность успеха в единичном испытании. Вместе с тем, во многих задачах приходится находить вероятности P_n,p(k) при больших значениях n. Это может вызвать значительные вычислительные трудности ввиду громоздкости биномиальных коэффициентов   и необходимости возводить числа p и (1 − p) в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями.

Теорема Пуассона:

Пусть  ,   таким образом, что , где a > 0 - заданное число. Тогда для любого фиксированного k

.

Другими словами, в описанном предельном переходе биномиальные вероятности P_n,p(k) аппроксимируются пуассоновским распределением.

Доказательство:

Для краткости будем считать, что  , p = a / n.Тогда   , поскольку выражение в квадратных скобках стремится к единице, если k фиксировано, а  .

Билет 23

Теорема Муавра-Лапласа:

Пусть ν_n – число успехов в последовательности из n независимых испытаний Бернулли с вероятностью успеха в единичном испытании p. Пусть  .При 

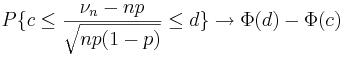 (2), где  .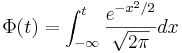

Замечание 1.

Функция Φ(t), появившаяся в этой теореме, называется функцией распределения стандартного нормального закона. Длязначений этой функции существуют подробные таблицы. Отметим, что онане зависит ни от каких параметров. Следовательно, предел в теореме Муавра-Лапласа является универсальным, так как он не зависит отпараметра p, который имеется в допредельном выражении.На самомделе, эта теорема является частным случаем другой, еще более универсальнойцентральной предельной теоремы.

Замечание 2.

Чтобы понять смысл выражения 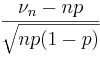  (3), необходимо вспомнить, что   и  . Таким образом, это выражение имеет вид  . Легко видеть, что  , а  .

Преобразование(3) называется центрированием и нормированием случайной величины ν_n.

Замечание 3.

В предельном переходе « , «p фиксировано» каждая «индивидуальная» вероятность P_n,p(k) стремится к нулю. Асимптотика этого стремления описывается так называемой локальной предельной теоремой. Что же касается интегральной предельной теоремы Муавра-Лапласа, то можно сказать, что она описывает предельное поведение сумм большого числа таких малыхвероятностей. Действительно,

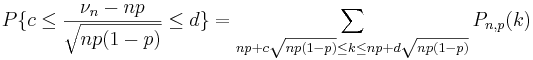
таким образом, в последней сумме содержится много (порядка  ) слагаемых.

Замечание 4.

Скорость сходимости в (2) хорошо изучена. Имеет место так называемая оценка Берри-Эссеена: Cуществует такое D > 0, что

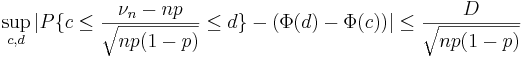.Билет 24

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Формальное математическое определение следующее: пусть   — вероятностное пространство, тогда случайной величиной называется функция  , измеримая относительно   и борелевской σ-алгебры на  . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения прерывной случайной величины Х может быть задан в следующих формах: • табличной; • аналитической; • графической.

Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Такую таблицу называют рядом распределения случайной величины Х.

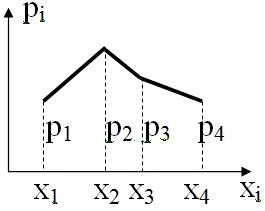
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению.

Для непрерывной случайной величины такой характеристики построить нельзя!!!

Для непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и есть некоторая функция от х.

Эта функция называется функцией распределения случайной величины Х и обозначается F(х): F(x) = P(X< x)

Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения.

Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Сформулируем некоторые общие свойства функции распределения: 1.F(x) – неубывающая функция своего аргумента т.е. при x₂ > x₁ F(x₂) > F(x₁); 2. F(–∞) = 0; 3. F(+∞) = 1.

Билет 25