Билет 2

§3. Необходимый признак сходимости ряда

Теорема. Если ряд сходится, то   un=0. Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел  =S. Тогда имеет место также равенство  =S, так как при n  и (n-1) . Вычитая почленно из первого равенства второе, получаем  -  =  = un=0, что и требовалось доказать. Следствие. Если  un≠0, то ряд u1+u2+…+un… расходится. Пример. Ряд   расходится, так как un= . Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что  un=0 не следует, что ряд сходится. Позже докажем, что так называемый гармонический ряд          (6) расходится, хотя  un= Этот ряд часто будет использоваться в дальнейшем.

Гармонический ряд

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

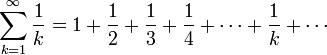
называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а₀ и знаменателем прогрессии, равным q.

Если |q| < 1, то существует предел суммы n первых членов этой прогрессии при неограниченном увеличении количества этих членов n:

В этом случае говорят о бесконечно убывающей геометрической прогрессии.

Ряд назван гармоническим, так как каждый его член, начиная со второго, является гармоническим средним двух соседних.

Обобщенный гармонический ряд

Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд^[1][3]

.

Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1^[3].

Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана:

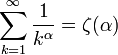
Для чётных это значение явно выражается через число пи, например,  , а уже для α=3 его значение аналитически неизвестно.

Билет 4.

Признаки сходимости числовых рядов

Необходимый признак сходимости числового ряда:  Если ряд   сходится, то  . Данный признак означает, что если  , то ряд расходится. Например,   расходится, так как  . Из выполнения условия   в общем случае не следует сходимость ряда  . Например, для ряда   (гармонический ряд), условие   выполнено, но данный ряд расходится. Достаточные признаки сходимости знакоположительных числовых рядов

Признаки сравнения

        Если  , и ряд   сходится, то сходится и ряд  .         Если  , и ряд   расходится, то расходится и ряд  . Признаки сравнения можно сформулировать в такой форме:         Если заданы ряды   и существует  , то ряды   сходятся либо расходятся одновременно. Признак Д’Аламбера Если существует   то:          при   ряд   сходится;         при   ряд   расходится. Радикальный признак Коши Если существует   то:          при   ряд   сходится;         при   ряд   расходится. Интегральный признак Коши Пусть задан ряд  , члены которого являются значениями непрерывной, положительной и монотонно убывающей функции f(x) на промежутке  . Тогда ряд   сходится, если сходится несобственный интеграл  . Если же   расходится, то ряд   также будет расходящимся. Знакочередующиеся и знакопеременные ряды

Признак Лейбница (достаточный признак сходимости знакочередующихсярядов) Ряд   сходится, если: . Знакопеременный ряд   называют абсолютно сходящимся, если сходится ряд  . Если ряд   сходится, а ряд   расходится, то ряд   называютсходящимся условно. Очевидно, что если ряд   сходится, то ряд   также сходится. Обратное утверждение в общем случае неверно.

Билет 6

Степенные ряды.

1. Основные понятия. Область сходимости.

Определение 1.1. Степенным рядом называется функциональный ряд вида

 (1.1) где a₀, a₁, a₂, …,a_n,…, а также x₀ – постоянные числа. Точку x₀ называют центром степенного ряда.

Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида

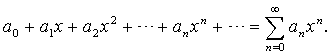 (1.2)

Такой ряд всегда сходится при x=0 и, значит, его область сходимости есть непустое множество.

Теорема 1.1. (теорема Абеля). Если степенной ряд (1.2) сходится при некотором  , где -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что   Наоборот, если ряд (12) расходится при  , то он расходится при всех значениях x таких, что   

Доказательство. Пусть числовой ряд

 (1.3) 

сходится. Поэтому   Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что   для всех n=0,1,2,…

Рассмотрим теперь ряд

 (1.4) 

предполагая, что   Так как 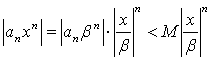  и при этом   то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда

 

(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.

Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при    Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.

Теорема Абеля позволяет дать описание области сходимости степенного ряда.

Теорема 1.2. Для степенного ряда (1.2) возможны только три случая:

1)    ряд сходится в единственной точке x=0;

2)    ряд сходится при всех значениях x;

3)    существует такое R>0, что ряд сходится при всех значениях x, для которых   и расходится при всех x, для которых   

Билет 7.

Определение 1.2. Интервал (-R,R), где число R определено в теореме 1.2, называется интервалом сходимости ряда (1.2), а число R – радиусом сходимости этого ряда.

Понятие радиуса сходимости будет распространяться на все три случая в теореме (3.2): для этого в случае 1 условимся считать R=0, а в случае 2 

На практике радиус сходимости степенного ряда чаще всего определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда (1.2) отличны от нуля и существует предел 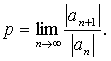  Тогда радиус сходимости находится по формуле 

Действительно, в силу признака Даламбера ряд

сходится, если число

 

меньше 1, и расходится, если этот предел больше 1. Иначе говоря, ряд сходится для всех x таких, что 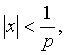  и расходится при   Это и означает, что число   является радиусом сходимости ряда (1.2).

Билет 9.

Страница: 6 из 7;   <<назад ^ вперед>> §8. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена 1. Разложение функции f(x)=ex в ряд Маклорена. f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex. f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1. Составим для функции f(x)=ex формально ряд Маклорена: 1+  . Найдём области сходимости этого ряда.  при любых x, следовательно, областью сходимости ряда является промежуток  (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то    при любых х и тем более   при любых х. Так как f(n+1)(x)=ex и f(n+1)(с)=eс, то  =ec =0. Таким образом, имеет место разложение при x (-∞;+∞) ex=1+  .     (32) 2. Разложение функции f(x)=sinx в ряд Маклорена. Вычислим производные данной функции. f′(x)=cosx=sin(x+ ), f″(x)=-sinx=sin(x+ ), f″′(x)=-cosx=sin(x+ ), f(4)(x)=sinx=sin(x+ ), …, f(n)(x)=sin(x+ ), … . Вычислим значения f(x) и производных в точке 0:f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f(4)(0)=0, …, f(2n-1)(0)=(-1)n-1, f(2n)(0)=0. Исследуем остаточный член ряда. |Rn(x)|= =  так как |sin(c+(n+1) |≤1. Переходя к пределу при n→∞, получаем   следовательно,   и  . Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x (-∞;+∞): sinx=x-  .             (33) 3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при        x (-∞;+∞): cosx=1-  .            (34) 4. Биномиальный ряд. Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные:f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1,f′(0)=m, f″(0)=(m-1)m,  f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … . Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что  . Таким образом, при x (-1;1) имеет место разложение: (1+x)m=1+ + + + +…+  .            (35) Ряд (35) называется биномиальным рядом. 5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3,f(4)(x)=-1.2.     .3.x-4=-3!x-4, …,  f(n)(x)=(-1)n-1.  .(n-1)!x-n, … . При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … . Можно показать, что областью сходимости ряда является промежуток (0;2] и что  . Таким образом, при x (0;2] имеет место разложение: lnx= .             (36) Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.   Примеры. 1. Разложить в степенной ряд функцию  . В формуле (32) сделаем замену переменной x=-t2, получим  при            t (-∞;+∞). Переобозначая t на x, получим нужное разложение:  при            x (-∞;+∞).

Билет 10.

4 Некоторые приложения степенных рядов

4.1 Приближенное вычисление значений функции Пусть требуется вычислить значение функции  при   с заданной точностью  . Если функцию   в интервале (-R; R) можно разложить в степенной ряд и  , то точное значение   равно сумме этого ряда при  , т.е. ,а приближенное – частичной сумме  , т.е. .Точность этого равенства увеличивается с ростом п. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т. е. , где . Таким образом, ошибку   можно найти, оценив остаток ряда  . Для рядов лейбницевского типа .В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки   берут величину остатка этого нового ряда. Пример 15. Найти значение sin1с точностью до 0,001. Решение: Согласно формуле (3.5) . Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Taк как  , а  , то для нахождения значения   с точностью до 0,001 достаточно первых трех слагаемых: . Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin 1 примерно равно 0,84147.

4.2 Приближенное вычисление определенных интегралов Бесконечные ряды применяются также для приближенного вычисления определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции или нахождение первообразной сложно. Пусть требуется вычислить   с точностью до  . Если подынтегральную функцию  можно разложить в ряд по степеням х и интервал сходимости (-R;R) включит в себя отрезок [ а; ], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и ошибку при вычислении значений функций. Пример  17.  Вычислить интеграл  с точностью до  . Решение: Разложим подынтегральную функцию в ряд Маклорена, за­меняя х на  в формуле (3.4): ,  . 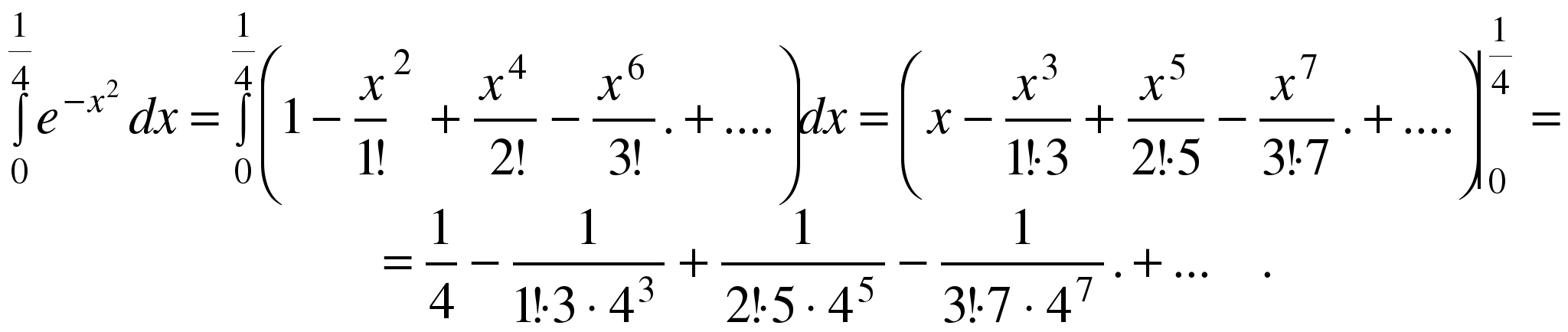Интегрируя обе части равенства (3.4) на отрезке  , лежащем внутри интервала сходимости  , получим: Получили ряд лейбницевского типа. Так как  , а  , то с точностью до 0,001 имеем: .

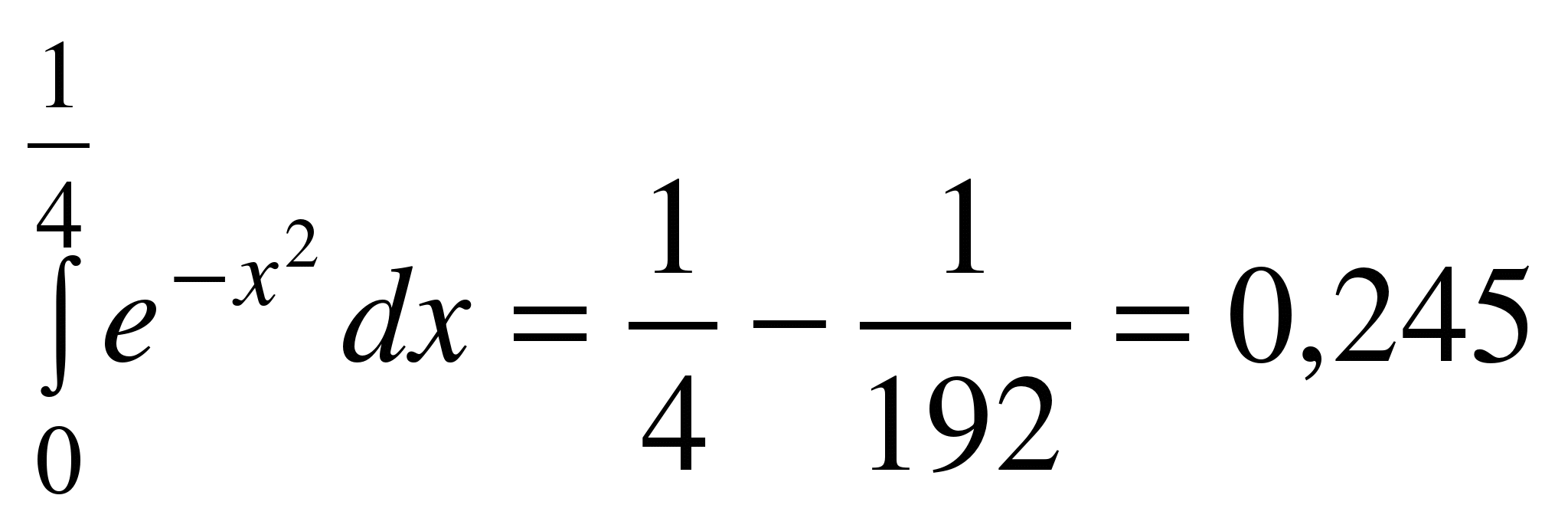Билет 11.

  Приближенное решение дифференциальных уравнений Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора. Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов. Пусть, например, требуется найти решение уравнения , (4.1) удовлетворяющее начальным условиям: ,  . (4.2)

Билет 12.

Пусть мы провели испытание N раз, R раз выпала решка, O = N – R раз выпал орел.

Предположим, что при большом числе испытаний N отношение   стремится к некоторой постоянной величине. Назовём её вероятностью p наступления события.

Часто вероятность, которая в нашем определении заключена в интервале 0 ≤ p ≤ 1, выражают в процентах, умножая число p на 100 %.

Иногда вероятность события можно предсказать из соображений симметрии. Например, при бросании «идеального» игрального кубика выпадение любой грани равновозможно (равновероятно). Всего граней 6, значит, вероятность выпадения i-й грани p (A_i) = p (A₁) = p (A₂) = p (A₃) = p (A₄) = p (A₅) = p (A₆) = 1/6.

Если мы имеем дело с измеримыми случайными величинами, например, измеряем в течение нескольких лет количество снега, выпавшего за день, то понятие вероятности тоже можно ввести. Для этого запишем результаты измерения в таблицу с точностью, например, в сантиметр и подсчитаем относительную частоту появления того или иного значения. Например, вероятность того, что выпадет 3 см снега, – 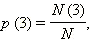  где N (3) – количество дней, в каждый из которых выпало 3 см, N – общее количество дней, в которые проводились измерения.

Для того чтобы найти вероятность события A, происходящего в серии испытаний, нужно:

1. найти число N всех возможных исходов (элементарных событий);

2. принять предположение о равновероятности этих исходов;

3. найти количество N (A) тех исходов, в которых наступает событие A;

4. найти частное   оно и будет равно вероятности p (A) наступления события A.

В этой очевидной инструкции есть очень важный пункт о равновероятности исходов. Проиллюстрируем его на примерах.

Билет 13.

.2.1 Схема выбора без возвращений

Упорядоченные совокупности (последовательный выбор)

Допустим, что эксперимент состоит в том, что из генеральной сово-

купности последовательно выбирают k элементов и располагают их в по-

рядке выбора. Отобранный элемент перед отбором следующего не возвра-

щается в генеральную совокупность. Такой выбор называется размеще-

нием k элементов из n элементов, размещением из n элементов по k

элементов, или последовательным выбором k элементов из n элементов

без возвращения.

Определение 6. Произведение всех натуральных чисел от 1 до n назы-

вается факториалом и обозначается n! (читается "n факториал"):

n! = 1 · 2 · 3 · . . . · n

Для удобства условились считать, что 0! = 1. Факториал есть стремительно

возрастающая функция натурального аргумента, действительно

n = 1 n! = 1! = 1

n = 2 n! = 2! = 1 · 2 = 2

n = 3 n! = 3! = 1 · 2 · 3 = 6

n = 4 n! = 4! = 1 · 2 · 3 · 4 = 24

n = 5 n! = 5! = 1 · 2 · 3 · 4 · 5 = 120

n = 6 n! = 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720

n = 7 n! = 7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5 040

n = 8 n! = 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40 320

10n = 9 n! = 9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362 880

n = 10 n! = 10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3 628 800

Определение 7. Перестановкой из n элементов называется размещение

из n элементов по n элементов.

Так как каждая перестановка содержит все n элементов

множества, то различные перестановки отличаются друг от друга

только порядком следования элементов.

Число всех перестановок множества из n элементов, обозначаемое

Pn, вычисляется по формуле:

Pn = n! (2)

Действительно, Pn = An

Билет 15.

Случайные события и действия над ними. Виды случайных событий. Комбинации событий Пространство элементарных событий.

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра — но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.

Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:

а) достоверное событие — событие, которое всегда происходит при проведении опыта;

б) невозможное событие — событие, которое в результате опыта произойти не может;

в) случайное событие — событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным — выпадение 10 очков, а случайным — выпадение 3 очков.

Билет 16

Вероятность событий

При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.

Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.

Если все события, которые могут произойти в результате данного опыта,

а) попарно несовместны;

б) равновозможны;

в) образуют полную группу,

то говорят, что имеет место схема случаев.

Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов).

Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:

- классическое определение вероятности.

Свойства вероятности.

Из определения 1.8 вытекают следующие свойства вероятности:

1. Вероятность достоверного события равна единице.

Доказательство. Так как достоверное событие всегда происходит в результате опыта, то все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно,

Р(А) = 1.

2. Вероятность невозможного события равна нулю.

Доказательство. Для невозможного события ни один исход опыта не является благопри-ятным, поэтому т = 0 и р(А) = 0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Доказательство. Случайное событие происходит при некоторых исходах опыта, но не при всех, следовательно,  0 < m < n, и из (1.1) следует, что 0 < p(A) < 1.

Билет 17