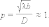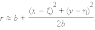Описание

Принцип Гюйгенса — Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Густав Кирхгоф придал принципу Гюйгенса — Френеля строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа (см. метод Кирхгофа).

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Дальнейшим обобщением и развитием принципа Гюйгенса — Френеля является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.

Дифракция Френеля. Размер препятствия порядка размера зоны Френеля. Их отношение оказывается порядка единицы:

(2.10)

Безразмерный параметр p называют волновым параметром. В этом случае справедливо френелевское приближение - в фазовом множителе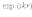 расстояние r заменяют приближенным выражением

(2.11)

Амплитудный множитель заменяют приближенным выражением 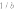, не зависящим от переменных интегрирования (при условии, что размер препятствия мал по сравнению с расстоянием до плоскости наблюдения). Указанные выше приближения используются при рассмотрении дифракции на экранах с осевой симметрией и на одномерных препятствиях.

Таким образом, в области френелевской дифракции (так называемая ближняя волновая зона) выражение (2.9) записывается в виде

(2.12)

2. Дифракция Фраунгофера. Размер препятствия много меньше размера зоны Френеля и, следовательно,

(2.13)

Неравенство (2.13) означает, что дифракционная картина наблюдается на достаточно удаленном экране (в пределе – на бесконечности). В этом случае радиусы-векторы , проведенные от различных точек экрана к точке наблюдения практически параллельны друг другу. Это обстоятельство резко упрощает фазовые соотношения. В области дифракции Фраунгофера в фазовом множителе можно приближенно положить

(2.14)

где 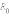– расстояние от центра экрана до точки наблюдения Р. В амплитудном множителе, как и в случае френелевской дифракции, выражение заменяют на . В области дифракции Фраунгофера

(2.15)

Следует подчеркнуть, что выражение (2.15) имеет вид двумерного преобразования Фурье функции 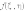(см. главу 1.2.3) - граничного возмущения в плоскости z = 0. Область дифракции Фраунгофера принято называть дальней волновой зоной.

Таким образом, критерием наблюдения дифракционных картин различного вида может служить значение волнового параметра 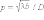. При наблюдается френелевская дифракция. Характерная качественная особенность френелевских дифракционных картин состоит в том , что область наблюдения дифракции приблизительно совпадает с границами геометрической тени. Например, при освещении плоской волной отверстия диаметра D в непрозрачном экране, размер дифракционной картины в плоскости z = b окажется порядка D. 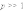При наблюдается дифракция Фраунгофера. В этом случае дифракционная картина значительно шире размеров геометрической тени. Второй важной особенностью фраунгоферовских дифракционных картин, в отличие от френелевской дифракции, является то, что при разных положениях плоскости наблюдения дифракционные картины подобны друг другу; при переходе к другой плоскости наблюдения изменяется только масштаб картины. По этому признаку наблюдаемые на экране дисплея дифракционные картины легко можно отнести к френелевской или фраунгоферовой дифракции.

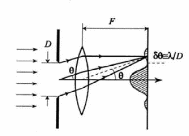
Отметим здесь, что фраунгоферова дифракция может наблюдаться в фокальной плоскости линзы (см. главу 8). Параллельный пучок лучей, распространяющийся под углом к оси (рис. 2.11), сводится линзой в некоторой точке фокальной плоскости без нарушения фазовых соотношений (таутохронизм). Поэтому распределение поля в фокальной плоскости в некотором масштабе воспроизводит дифракционную картину, которую можно наблюдать в отсутствие линзы на достаточно удаленной плоскости наблюдения. В оптических инструментах, как правило, наблюдается дифракция Фраунгофера.

Рисунок 2.11. Наблюдение дифракции Фраунгофера в фокальной плоскости линзы.

Положение точки наблюдения при дифракции Фраунгофера удобно задавать с помощью угловых координат. В частности при дифракции на щели ширины D распределение интенсивности, рассчитанное с помощью (2.15), имеет вид

(2.16)

Это распределение качественно изображено на рис. 2.11.

Первый нуль функции наблюдается при условии . Полагая дифракционные углы достаточно малыми и обозначая полуширину главного дифракционного максимума через , получаем соотношение

(2.17)

Соотношение (2.17) является классическим аналогом соотношения неопределенности Гейзенберга в квантовой физике .

Отметим в заключение, что неравенство можно рассматривать как критерий геометрической оптики. В этом случае плоскость наблюдения располагается достаточно близко от препятствия (например, экрана с отверстием). Дифракционные явления практически незаметны, и в плоскости наблюдения возникает геометрическая тень препятствия с четко обозначенными границами.

_25. Разбиение волнового фронта на зоны Френеля. Дифракция Френеля на круглом отверстии. Спираль Френеля.