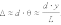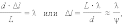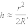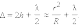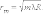Описание

Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).

Классическое объяснение явления

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

 — max, где -   любое целое число,   -  длина волны.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

 — min, где -   любое целое число,   -  длина волны.

Для учета того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода. Разность оптических длин пути называется оптической разностью хода.

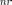 — оптическая длина пути,

 — оптическая разность хода.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на , этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы. Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

где

R — радиус кривизны линзы;

k = 2, 4, …;

λ — длина волны света в вакууме;

n — показатель преломления среды между линзой и пластинкой.

Использование

Кольца Ньютона используются для измерения радиусов кривизны поверхностей, для измерения длин волн света и показателей преломления. В некоторых случаях (например, при сканировании изображений на плёнках или оптической печати с негатива) кольца Ньютона представляют собой нежелательное явление.

_23. Классическая схема интерференции и примеры ее реализации. Ширина интерференционной полосы.

классические интерференционные схемы: зеркало Ллойда, бизеркала и бипризма Френеля. В этих схемах реализуется идея опыта Юнга: получить два когерентных источника для наблюдения интерференции путем деления пучка света, испускаемого одним источником, на два пучка.

Максимумы интерференции наблюдаются в тех точках, в которые интерферирующие волны приходят в одинаковой фазе, т.е. при d = 2pn, где n – целое число, положительное или отрицательное. Тогда разность хода равна:

D = nl.                                                                                                         

Минимумы наблюдаются в тех точках, в которые волны приходят в противофазе. Для этих точек разность фаз , что соответствует разности хода

.                                                                                             

Для того чтобы максимумы и минимумы были более четкими, амплитуды складываемых колебаний должны быть равными. При наблюдении интерференции необходимо, чтобы разность хода волн была менее длины цуга. Иначе будут складываться колебания, создаваемые разными цугами, и условие когерентности выполняться не будет.

Рассмотрим схему Юнга. Источниками света в оригинальном опыте Юнга являлись две узкие щели, интерференция наблюдалась на удаленном экране. На рис. 1 S₁ и S₂ – источники света, S₁М и S₂М – расстояния от источников до точки наблюдения М. Проведем S₁А перпендикулярно S₂М. Треугольники S₁S₂А и ВМО подобны. В практически применяемых интерференционных схемах угол между интерферирующими лучами S₁МS₂ мал (порядка долей градуса), т.е. расстояние от источников до экрана гораздо больше расстояния между самими источниками. Поэтому S₂А приближенно равна разности хода D = S₂М - S₁М.

Из подобия треугольников имеем: D/d » x/L, откуда

x = LD/d,                                                                                                      

где х = ОМ – координата точки наблюдения на экране, d = S₁S₂ – расстояние между источниками, L = ВО – расстояние от источников до экрана.

Если в точке М наблюдается максимум, то разность хода лучей в этой точке равна целому числу длин волн. Тогда согласно (5) координаты точек максимумов равны  (n – целое число: n = 0, ±1, ±2, ±3,…, называемое порядком интерференционного максимума). Между максимумами находятся минимумы. Расстояние между соседними максимумами и между соседними минимумами одинаково и равно

.                                                                                                    

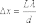Если на пути одного из лучей, например, верхнего, поставить тонкую прозрачную пластинку с показателем преломления n и толщиной h, то между лучами возникнет дополнительная оптическая разность хода , т.к. один из лучей проходит путь h в воздухе, а второй это расстояние проходит в веществе пластинки. Вследствие этого вся интерференционная картина сместится в ту сторону, где находится пластина, т.е. в нашем примере вверх. Если дополнительная разность хода равна длине волны, то произойдет смещение на ширину одной интерференционной полосы. Если произошло смещение картины на N полос (N может быть и дробным), то дополнительная оптическая разность хода:

.                                                                                             

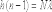Эта формула позволяет, зная λ, определить как показатель преломления пластины (если известна толщина), так и ее толщину при известном показателе преломления.

Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:

При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,

где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S₁ и S₂ равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 10⁵ нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.

Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек.

В эксперименте Ньютона (рис. 3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h, можно приближенно получить:

где r – смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло–воздух, а вторая – от границы воздух–стекло. Во втором случае происходит изменение фазы колебаний отраженной волны на π, что эквивалентно увеличению разности хода на λ / 2. Поэтому

При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум – темное пятно. Радиусы r_m последующих темных колец определяются выражением

Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы.

_24. Дифракция света. Принцип Гюйгенса-Френеля. Два вида дифракции (Френеля и Фраунгофера).

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и размером ширины волнового фронта , либо непрозрачного экрана на пути его распространения, либо неоднородностей структуры самой волны.

Поскольку в большинстве случаев, имеющих практическое значение, это ограничение ширины волнового фронта имеет место всегда, постольку явление дифракции всегда сопровождает любой процесс распространения волн.

Так, именно явлением дифракции задаётся предел разрешающей способности любого оптического прибора, создающего изображение, который невозможно преступить принципиально при заданной ширине спектра используемого для построения изображения излучения^.

В ряде случаев, в особенности при изготовлении сложных оптических систем, разрешающая способность ограничивается не дифракцией, но аберрациями, как правило, возрастающими при увеличении диаметра объектива. Отсюда происходит известное фотографам явление увеличения до определённых пределов качества изображения при диафрагмировании объектива.

При распространении излучения в оптически неоднородных средах дифракционные эффекты заметно проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды сравним с длиной волны, в таком случае дифракция проявляет себя в виде эффекта рассеяния волн.

Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.

Дифракция волн может проявляться:

• в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;

• в разложении волн по их частотному спектру;

• в преобразовании поляризации волн;

• в изменении фазовой структуры волн.

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.