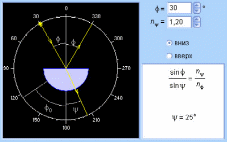
Свойства электромагнитной волны.
Частота - количество оборотов биона в единицу времени. Скорость света - скорость передачи вращений от одного биона к другому. Фаза - расположение одного из полюсов биона относительно линии распространения электромагнитной волны.
Электромагнитные волны поперечны
– векторы
и
перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны
Электромагнитные волны распространяются в веществе с конечной скоростью
|
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Длина волны λ в синусоидальной волне свявзана со скоростью υ распространения волны соотношением λ = υT = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
|
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
Вывод Максвелла о конечной скорости распространения электромагнитных волн находился в противоречии с принятой в то время теорией дальнодействия, в которой скорость распространения электрического и магнитного полей принималась бесконечно большой. Поэтому теорию Максвелла называют теорией близкодействия.
3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм.
|
Отсюда следует, что в электромагнитной волне модули индукции магнитного поля и напряженности электрического поля в каждой точке пространства связаны соотношением
|
4. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (wэ + wм)υSΔt. |
Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:
|
Подставляя сюда выражения для wэ, wм и υ, можно получить:
|
Поток энергии в электромагнитной волне
можно задавать с помощью вектора
направление
которого совпадает с направлением
распространения волны, а модуль равен
EB / μμ0. Этот вектор называют
вектором Пойнтинга.
В синусоидальной (гармонической) волне в вакууме среднее значение Iср плотности потока электромагнитной энергии равно
|
где E0 – амплитуда колебаний напряженности электрического поля.
Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м2).
Существование давления электромагнитных волн позволяет сделать вывод о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля в единичном объеме выражается соотношением
|
где wэм – объемная плотность электромагнитной энергии, c – скорость распространения волн в вакууме. Наличие электромагнитного импульса позволяет ввести понятие электромагнитной массы.
Для поля в единичном объеме
|
Отсюда следует:
|
Это соотношение между массой и энергией электромагнитного поля в единичном объеме является универсальным законом природы. Согласно специальной теории относительности, оно справедливо для любых тел независимо от их природы и внутреннего строения.
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.
Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент p (t) которого быстро изменяется во времени.
Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ
КОГЕРЕНТНОСТЬ
Важным свойством двух одновременно протекающих волновых процессов является их когерентность.
По определению когерентностью двух волновых процессов называется их согласованное протекание. В соответствии с этим определением две монохроматические волны одной частоты всегда будут когерентными. Другой пример когерентных волн представлен на рис. 4.4, изображающем две волны от одного источника монохроматических колебаний , одна из которых от источника распространяется в точку наблюдения по прямому пути, а вторая после отражения от границы раздела. Согласованность колебаний двух волн в точке наблюдения обусловлена тем, что они излучаются одним источником. Если поместить на пути распространения этих волн экран, то на нём, при определённых условиях о которых будет сказано ниже, будет можно наблюдать интерференционную картину, которая будет представлять собой чередование тёмных и светлых полос.
|
Рис. 4.4. |
Итак, согласованность протекания двух волновых процессов связывается с возможностью наблюдать их интерференционную картину волн, излучаемых их источниками. С другой стороны, как мы установили выше, при наблюдении интерференции в каждой точке экрана, с помощью которого она наблюдается, разность фаз должна иметь определённое значение и не меняться со временем. Предположим, что разность фаз колебаний интерферирующих источников волн меняется со временем. Для определённости будем полагать, что она увеличивается пропорционально времени. Тогда в точке экрана, где в какой то момент времени наблюдался интерференционный максимум, со времен разность фаз изменит своё значение за некоторый промежуток времени и в этой точке окажется выполненным условие минимума интерференционной картины. В результате зависимости разности фаз колебаний интерферирующих источников от времени их интерференционная картина будет меняться во времени, т. е. не будет стабильной. Это может затруднить наблюдение интерференции волн источников, а в ряде случаев наблюдение интерференции вообще может стать невозможным.
Таким
образом, два волновых процесса называются
когерентными, если средняя разность их
полных фаз
в
точке наблюдения
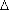с
координатами
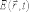не
зависит от времени наблюдения
:
|
(4.12) |
,где
-
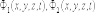соответственно полные фазы первой и
второй волны; черта над разностью фаз
означает её среднее значение по времени,
для определения которой может быть
использована формула (1.31).
В
соответствии с этим определением две
монохроматические электромагнитные
волны являются когерентными. Действительно,
рассмотрим для простоты две плоские
одинаково поляризованные монохроматические
электромагнитные волны одой частоты
,
распространяющиеся вдоль оси
выбранной
системы координат
с
колебаниями вдоль оси
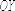векторов
напряжённости электрического поля
и
,
описываемых следующими выражениями:
|
Рис. 4.5. |
,
где
-
амплитуды волн;
-
их начальные фазы;
-
волновое число;
-
длина волны.
В
соответствии с этим выражением, используя
(4.12), найдём полные фазы
волн:
.
Определяя
разность полных фаз , получим
:
,
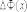убеждаемся, что она не зависит от времени. Следовательно, в соответствии с определением когерентности (4.12) рассматриваемые две плоские монохроматические волны одной частоты являются когерентными.
_18. Шкала электромагнитных волн. Оптический диапазон, видимый свет.
Наименование |
Длина, м |
Частота, Гц |
Сверхдлинные |
106-104 |
3*102- 3*104 |
Длинные (радиоволны) |
104-103 |
3*104- 3*105 |
Средние(радиоволны) |
103 -102 |
3*105- 3*106 |
Короткие(радиоволны) |
102-101 |
3*106- 3*107 |
Ультракороткие |
101-10-1 |
3*107- 3*109 |
Телевидение (СВЧ) |
10-1-10-2 |
3*109- 3*1010 |
Радиолокация (СВЧ) |
10-2-10-3 |
3*1010- 3*1011 |
Инфракрасное излучение |
10-3-10-6 |
3*1011- 3*1014 |
Видимый свет |
10-6-10-7 |
3*1014- 3*1015 |
Ультрафиолетовое излучение |
10-7-10-9 |
3*1015- 3*1017 |
Рентгеновское излучение(мягкое) |
10-9-10-12 |
3*1017- 3*1020 |
Гамма-излучение (жесткое) |
10-12-10-14 |
3*1020- 3*1022 |
Космические лучи |
≤10-14 |
≤3*1022 |
Спектр электромагнитных волн.
Электромагнитные
волны классифицируются по длине волны
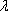или
связанной с ней частотой волны
.
Отметим также, что эти параметры
характеризуют не только волновые, но и
квантовые свойства электромагнитного
поля. Соответственно в первом случае
электромагнитная волна описывается
классическими законами, изучаемыми в
данном томе, а во втором - квантовыми
законами, изучаемыми в томе 5 настоящего
пособия.
Рассмотрим понятие спектра электромагнитных волн. Спектром электромагнитных волн называется полоса частот электромагнитных волн, существующих в природе.
Спектр электромагнитного излучения в порядке увеличения частоты составляют:
1) Радиоволны;
2) Инфракрасное излучение;
3) Световое излучение;
4) Рентгеновское излучение;
5) Гамма излучение.
Различные участки электромагнитного спектра отличаются по способу излучения и приёма волн, принадлежащих тому или иному участку спектра. По этой причине, между различными участками электромагнитного спектра нет резких границ.
Радиоволны изучает классическая электродинамика. Инфракрасное световое и ультрафиолетовое излучение изучает как классическая оптика, так и квантовая физика. Рентгеновское и гамма излучение изучается в квантовой и ядерной физике.
Рассмотрим спектр электромагнитных волн более подробно.
Радиоволны.
Радиоволны представляют собой электромагнитные волны, длины которых превосходят 0.1мм( частота меньше 3 1012гц = 3000 Ггц).
Радиоволны делятся на:
1. Сверхдлинные волны с длиной волны больше 10км( частота меньше 3 104гц=30кгц);
2. Длинные волны в интервале длин от10км до 1км( частота в диапазоне 3 104 гц -3 105гц=300кгц);
3. Средние волны в интервале длин от1км до 100м(частота в диапазоне 3 105 гц -3106гц=3мгц);
4. Короткие волны в интервале длин волн от 100м до 10м (частота в диапазоне 3106гц-3107гц=30мгц);
5. Ультракороткие волны с длиной волны меньше 10м(частота больше 3107гц=30Мгц).
Ультракороткие волны в свою очередь делятся на :
а) метровые волны;
б) сантиметровые волны;
в) миллиметровые волны;
г) субмиллиметровые или микрометровые.
Волны с длиной волны меньше, чем 1м(частота меньше чем 300мгц) называются микроволнами или волнами сверхвысоких частот(СВЧ - волны).
Из-за больших значений длин волн радиодиапазона по сравнению с размерами атомов распространение радиоволн можно рассматривать без учета атомистического строения среды, т.е. феноменологически, как принято при построении теории Максвелла. Квантовые свойства радиоволн проявляются лишь для самых коротких волн, примыкающих к инфракрасному участку спектра и при распространении т.н. сверхкоротких импульсов с длительностью порядка 10-12сек- 10-15сек, сравнимой со временем колебаний электронов внутри атомов и молекул.
Инфракрасное и световое излучения.
Инфракрасное, световое, включая ультрафиолетовое, излучения составляют оптическую область спектра электромагнитных волн в широком смысле этого слова. Близость участков спектра перечисленных волн обусловило сходство методов и приборов, применяющихся для их исследования и практического применения. Исторически для этих целей применяли линзы, дифракционные решетки, призмы, диафрагмы, оптически активные вещества, входящие в состав различных оптических приборов (интерферометров, поляризаторов, модуляторов и пр.).
С другой стороны излучение оптической области спектра имеет общие закономерности прохождения различных сред, которые могут быть получены с помощью геометрической оптики, широко используемой для расчетов и построения, как оптических приборов, так и каналов распространения оптических сигналов.
Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 210-6м= 2мкм до 10-8м=10нм (по частоте от1.51014гц до 31016гц). Верхняя граница оптического диапазона определяется длинноволновой границей инфракрасного диапазона, а нижняя коротковолновой границей ультрафиолета (рис.2.14).
|
Рис. 1.14. |
Ширина оптического диапазона по частоте
составляет примерно 18 октав1,
из которых на оптический диапазон
приходится примерно одна октава(
);
на ультрафиолет - 5 октав (
),
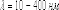на инфракрасное излучение - 11 октав (
).
В оптической части спектра становятся существенными явления, обусловленные атомистическим строением вещества. По этой причине наряду с волновыми свойствами оптического излучения проявляются квантовые свойства.
Рентгеновское и гамма излучение.
В области рентгеновского и гамма излучения на первый план выступают квантовые свойства излучения.
Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов.
Гамма излучение является следствием
явлений, происходящих внутри атомных
ядер, а также в результате ядерных
реакций. Граница между рентгеновским
и гамма излучением определяются условно
по величине кванта энергии
2,
соответствующего данной частоте
излучения.
Рентгеновское излучение составляют электромагнитные волны с длиной от50 нм до 10-3нм, что соответствует энергии квантов от 20эв до 1Мэв.
Гамма излучение составляют электромагнитные волны с длиной волны меньше 10-2нм, что соответствует энергии квантов больше 0.1Мэв.
Электромагнитная природа света.
Свет представляет собой видимый участок спектра электромагнитных волн, длины волн которых занимают интервал от 0.4мкм до 0.76мкм. Каждой спектральной составляющей оптического излучения может быть поставлен в соответствие определённый цвет. Окраска спектральных составляющих оптического излучения определяется их длиной волны. Цвет излучения изменяется по мере уменьшения его длины волны следующим образом: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Красный свет, соответствующий наибольшей длине волны, определяет красную границу спектра. Фиолетовый свет - соответствует фиолетовой границе.
Естественный свет не окрашен и представляет суперпозицию электромагнитных волн из всего видимого спектра. Естественный свет появляется в результате испускания электромагнитных волн возбужденными атомами. Характер возбуждения может быть различным: тепловой, химический, электромагнитный и др. В результате возбуждения атомы излучают хаотическим образом электромагнитные волны примерно в течении 10-8сек. Поскольку энергетический спектр возбуждения атомов достаточно широкий, то излучаются электромагнитные волны из всего видимого спектра, начальная фаза, направление и поляризация которых имеет случайный характер . По этой причине естественный свет не поляризован. Это означает, что "плотность" спектральных составляющих электромагнитные волны естественного света, имеющих взаимно перпендикулярные поляризации одинаково.
Гармонические электромагнитные волны
светового диапазона называются
монохроматическими. Для световой
монохроматической волны одной из главных
характеристик является интенсивность.
Интенсивность световой волны
представляет собой среднее значение
величины плотности потока энергии
(1.25)
переносимого волной:
|
(1.42) |
,
где
-
вектор Пойнтинга.
Расчет интенсивности световой, плоской,
монохроматической волны с амплитудой
электрического поля
в
однородной среде с диэлектрической
и
магнитной
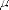проницаемостями
по формуле (1.35)
с учетом (1.30)
и (1.32)
дает :
|
(1.43) |
,
где
-
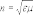коэффициент преломления среды;
-
волновое сопротивление вакуума.
Традиционно оптические явления рассматриваются с помощью лучей. Описание оптических явлений с помощью лучей называется геометрооптическим. Правила нахождения траекторий лучей, разработанные в геометрической оптике, широко используются на практике для анализа оптических явлений и при построении различных оптических приборов.
Дадим определение луча, исходя из
электромагнитного представления
световых волн. Прежде всего, лучи - это
линии, вдоль которых распространяются
электромагнитные волны. По этой причине
луч - это линия, в каждой точке которой
усредненный вектор Пойнтинга
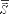электромагнитной
волны направлен по касательной к этой
линии.
В однородных изотропных средах направление
среднего вектора Пойнтинга
совпадает
с нормалью к волновой поверхности
(эквифазной поверхности), т.е. вдоль
волнового вектора
.
Таким образом, в однородных изотропных средах лучи перпендикулярны соответствующему волновому фронту электромагнитной волны.
Для примера рассмотрим лучи, испускаемые точечным монохроматическим источником света. С точки зрения геометрической оптики из точки источника исходит множество лучей в радиальном направлении. С позиции электромагнитной сущности света из точки источника распространяется сферическая электромагнитная волна. На достаточно большом расстоянии от источника кривизной волнового фронта можно пренебречь, считая локально сферическую волну плоской. Разбивая поверхность волнового фронта на большое количество локально плоских участков, можно через центр каждого участка провести нормаль, вдоль которого распространяется плоская волна, т.е. в геометрооптической интерпретации луч. Таким образом, оба подхода дают одинаковое описание рассмотренного примера.
Основная задача геометрической оптики состоит в нахождении направления луча (траектории). Уравнение траектории находится после решения вариационной задачи нахождения минимума т.н. действия на искомых траекториях. Не вдаваясь в подробности строгой формулировки и решения указанной задачи, можно полагать, что лучи представляют собой траектории с наименьшей суммарной оптической длиной. Данное утверждение является следствием принципа Ферма.
Вариационный подход определения
траектории лучей может быть применен
и к неоднородным средам, т.е. таким
средам, у которых показатель преломления
является
функция координат точек среды. Если
описать функцией
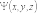форму
поверхности волнового фронта в
неоднородной среде, то её можно найти
исходя из решения уравнения в частных
производных, известного как уравнение
эйконала, а в аналитической механике
как уравнение Гамильтона - Якоби:
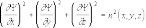
Таким образом, математическую основу геометрооптического приближения электромагнитной теории составляют различные методы определения полей электромагнитных волн на лучах, исходя из уравнения эйконала или каким - либо другим способом. Геометрооптическое приближение широко используется на практике в радиоэлектронике для расчета т.н. квазиоптических систем.
В заключение заметим, что возможность описать свет одновременно и с волновых позиций путем решения уравнений Максвелла и с помощью лучей, направление которых определяется из уравнений Гамильтона - Якоби, описывающих движение частиц, является одним из проявлений дуализма света, приведшего, как известно, к формулировке основных принципов квантовой механики.
1) Октавой по определению называется диапазон частот между произвольной частотой w и её второй гармоникой, равной 2w.
2) h=6.6310-34 Джсек - постоянная Планка.
Оптика
_19. Основные законы геометрической оптики и отклонения от них. Волновые свойства света.
Геометрическая оптика рассматривает излучение как тонкие пучки света – лучи, в однородной среде распространяющиеся прямолинейно. Геометрическая оптика базируется на четырех аксиомах.
Лучи света распространяются независимо друг от друга. Суммарная интенсивность двух пучков равна сумме интенсивностей каждого пучка в отсутствие другого (принцип суперпозиции). Нарушение этой аксиомы сопровождается интерференцией, изучение которой выходит за рамки геометрической оптики.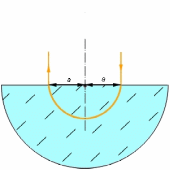
Рисунок 2.1.2.1.
Геометрическая оптика допускает искривление лучей света в оптически неоднородных средах. На приведенном рисунке показатель преломления вещества в полусфере зависит от расстояния до ее центра по формуле n = n0 / (1 + (r/r0)2). Луч, падающий нормально на расстоянии r0 от центра полусферы, выйдет с другой стороны полусферы на том же расстоянии от центра
В однородной среде лучи света распространяются прямолинейно. В начале XIX века было открыто явление огибания светом препятствий, получившее название дифракции.
Закон отражения света: угол падения светового луча равен углу его отражения. Падающий и отраженный лучи, а также перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
Закон Снеллиуса: отношение синуса угла падения к синусу угла преломления есть величина, постоянная для двух сред:
Падающий и преломленный лучи, а также перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
|
Модель 2.1. Законы геометрической оптики |
Для упрощения расчетов в геометрической оптике часто используется приближение параксиального пучка лучей. Суть его в том, что рассматриваются только лучи, распространяющиеся вблизи оптической оси системы и образующие очень малые углы с этой осью и нормалями к отражающим и преломляющим поверхностям системы. Когда угол между оптической осью и падающим лучом мал, можно считать, что sin φ ≈ tg φ ≈ φ. Отклонения от законов параксиальной оптики в оптических приборах приводят к появлению различных аберраций.
|
Рисунок 2.1.2.2. Пучок параллельных лучей в приближении параксиальной оптики собирается в фокусе сферического зеркала |
Пучок параллельных лучей, распространяющийся
вдоль оптической оси, в приближении
параксиальной оптики после отражения
от сферического зеркала соберется в
одной точке, называемой фокусом
сферического зеркала. Эта точка отстоит
от центра сферы на расстояние
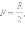где
R – радиус сферы. Связь между расстоянием
до предмета (f) и расстоянием до изображения
(d) дается формулой:
|
|
Рисунок 2.1.2.3. При прохождении через положительную (выпуклую) линзу пучок параллельных лучей собирается в одной точке |
Параллельные пучки собирает в точку не только зеркало, но и выпуклая линза. Если расстояние до фокуса линзы равно F, то формула линзы записывается следующим образом:
|
|
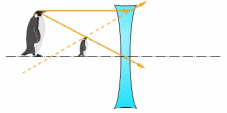
Рисунок 2.1.2.4. Рассеивающая (вогнутая) линза дает прямое мнимое изображение предмета |
Если изображение источника стало мнимым и находится с той же стороны от линзы, что и источник, то предыдущая формула примет вид:
|
|
Рисунок 2.1.2.5. Угловое увеличение линзы |
Линейным увеличением оптической системы называется отношение величины изображения предмета к величине самого предмета. В астрономии чаще применяют понятие угловое увеличение:
|
Отражение света от гладких полированных поверхностей называется зеркальным. Альбедо – доля упавшего излучения, отраженного поверхностью. Поскольку доля отраженного излучения всегда меньше падающего, альбедо всегда меньше 1. Чем больше альбедо, тем большая часть излучения отражена.
Белые тела (например, снег) почти полностью отражают свет, а черные (например, уголь) – почти полностью поглощают.
Самый светлый астероид – 44 Низа – имеет альбедо 0,38, а почти черный астероид – 52 Европа – имеет альбедо 0,03.
|
Рисунок 2.1.2.6. Планета Меркурий отражает в несколько раз больше света, чем каменный уголь. Ее альбедо 0,11 |
Границы применимости геометрической оптики. Если длина волны излучения много меньше линейных размеров тех объектов, с которыми взаимодействует свет ( << L), то можно рассматривать свет как совокупность лучей, распространение которых подчиняется простым законам:
Лучи света распространяются прямолинейно.
Справедлив закон отражения.
Справедлив закон преломления.
При этих условиях можно не учитывать волновые свойства света (явления дифракции и интерференции). Основные понятия геометрической оптики. Геометрическая оптика изучает изображения объектов, получаемые после прохождения отраженных от объекта лучей света через оптические устройства. Эти устройства могут быть двух типов: отражательные (зеркала) и преломляющие (линзы). Конечно, сложное оптическое устройство может быть произвольной комбинацией зеркал и линз. Всякий предмет, изображение которого дает оптическое устройство, может быть представлен как совокупность светящихся точек, испускающих лучи света. Таким образом, чтобы в рамках геометрической оптики построить изображение предмета, следует понять, как распространяются отдельные лучи от точечных источников. Ось симметрии оптического устройства, соединяющая точечный объект с центром кривизны зеркала или линзы, называется главной оптической осью. Геометрическая оптика рассматривает отображение пучка лучей, идущих вблизи от главной оптической оси (если это условие не выполнено, возникают отклонения от законов геометрической оптики - оптические аберрации). Если изображение точки, находящейся над оптической осью, также находится над оптической осью, оно называется прямым. В противном случае изображение называется обратным. Увеличением оптического устройства m называется отношение размера изображения к размеру объекта, причем по соглашению увеличение считается положительным, если изображение прямое, и отрицательным - если изображение обратное. Сферические зеркала.
Правила:
Расстояние до объекта s считается положительным, если объект находится на той же стороне относительно поверхности зеркала, что и падающий свет. В противном случае расстояние s считается отрицательным.
Расстояние до изображения s' считается положительным, если изображение находится на той же стороне зеркала, что и отраженный свет. Такое изображение называется действительным. В противном случае s' считается отрицательным, а изображение называется мнимым.
Радиус кривизны зеркала R положителен, если центр кривизны находится на той же стороне по отношению к поверхности зеркала, что и отраженный свет. В ином случае радиус кривизны отрицателен. Знак фокусного расстояния сферического зеркала f = R/2 определяется знаком R.
Применяя
закон отражения света, можно вывести
формулу сферического зеркала, связывающую
расстояния от объекта и от изображения
до зеркала с фокусным расстоянием или
радиусом кривизны зеркала:
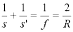(3.1)
Особенности хода главных лучей:
Луч, проходящий через центр кривизны зеркала, отражается назад.
Луч, проходящий через фокус зеркала, отражается и идет параллельно главной оптической оси.
Луч, идущий параллельно главной оптической оси, отражаясь от зеркала, проходит через фокус.
Формула
для зеркала справедлива во всех случаях:
а)
- вогнутое зеркало; увеличение
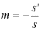(3.2)
б)
- выпуклое зеркало; изображение прямое
и мнимое;
в)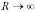
- плоское зеркало, т.е. изображение
обратное; в этом случае из формулы
следует, что s' = - s. Так как изображение
в плоском зеркале мнимое, то расстояние
от зеркала до изображения следует
считать отрицательным. Поэтому увеличение
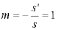Линзы.
Для того, чтобы можно было применять
законы геометрической оптики к
преломляющим линзам, эти линзы должны
быть тонкими (в противном случае возникают
сильные искажения изображения,
обусловленные разностью хода лучей в
разных частях линзы).
Два главных типа линз:
Собирающая линза, которая собирает падающий на нее пучок света, параллельный оптической оси, в одной точке по другую сторону линзы, называемой главным фокусом; расстояние от центра линзы до этой точки называется фокусным расстоянием f > 0;
Рассеивающая линза, которая рассеивает падающий на нее пучок света, параллельный главной оптической оси так, что при продлении всех лучей они собираются в одной точке - фокусе, расположенном на той же стороне линзы, что и падающий пучок света; при этом фокусное расстояние f < 0.
В
отличие от зеркал, линзы имеют два фокуса
по обе стороны линзы. Основная формула
для линзы любого типа имеет тот же вид,
что и для зеркала:
Все
соглашения о знаках величин s, s'
и f сохраняют силу, если только
дополнить их условием, что s' > 0,
когда действительное изображение
находится по другую сторону линзы.
Увеличение линзы также определяется
прежней формулой
Особенности хода главных лучей в собирающей линзе:
Луч, проходящий через центр линзы, не искажается.
Луч, проходящий через передний фокус линзы (тот фокус, который находится по ту же сторону, что источник), идет после преломления параллельно главной оптической оси.
Луч, идущий параллельно главной оптической оси, после преломления проходит через задний фокус линзы.
Величина, обратная фокусному расстоянию
линзы, называется оптической силой
линзы D:
Размерность:
[D] = диоптрия (дптр). Линза с фокусным
расстоянием 1 м имеет оптическую силу
1 дптр.
Волновые свойства света. Электромагнитная
теория света.
Свет
— это электромагнитные волны в интервале
частот
,
воспринимаемых человеческим глазом,
т. е. длин волн в интервале 380 - 770
нм.
Свету присущи все свойства электромагнитных
волн: отражение, преломление, интерференция,
дифракция, поляризация. Свет может
оказывать давление на вещество,
поглощаться средой, вызывать явление
фотоэффекта. Имеет конечную скорость
распространения в вакууме 300 000 км/с, а
в среде скорость убывает.
Наиболее наглядно волновые свойства
света обнаруживаются в явлениях
интерференции и дифракции. Интерференцией
света называют пространственное
перераспределение светового потока
при наложении двух (или нескольких)
когерентных световых волн, в результате
чего в одних местах возникают максимумы,
а в других минимумы интенсивности
(интерференционная картина). Интерференцией
света объясняется окраска мыльных
пузырей и тонких масляных пленок на
воде, хотя мыльный раствор и масло
бесцветны. Световые волны частично
отражаются от поверхности тонкой пленки,
частично проходят в нее. На второй
границе пленки вновь происходит частичное
отражение волны (рис. 46). Световые волны,
отраженные двумя поверхностями тонкой
пленки, распространяются в одном
направлении, но проходят разные пути.
При разности хода I, кратной целому числу
длин волн,
При разности хода, кратной нечетному
числу полуволн,
,
наблюдается интерференционный минимум.
Когда выполняется условие максимума
для одной длины световой волны, то оно
не выполняется для других волн. Поэтому
освещенная
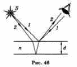белым светом тонкая цветная прозрачная
пленка кажется окрашенной. Явление
интерференции в тонких пленках применяется
для контроля качества обработки
поверхностей просветления оптики.
При прохождении света через малое
круглое отверстие на экране вокруг
центрального светлого пятна наблюдаются
чередующиеся темные и светлые кольца;
если свет проходит через узкую щель, то
получается картина из чередующихся
светлых и темных полос.
Явление отклонения света от прямолинейного
направления распространения при
прохождении у края преграды называют
дифракцией света. Дифракция объясняется
тем, что световые волны, приходящие в
результате отклонения из разных точек
отверстия в одну точку на экране,
интерферируют между собой. Дифракция
света используется в спектральных
приборах, основным элементом которых
является дифракционная решетка.
Дифракционная решетка представляет
собой прозрачную пластинку с нанесенной
на ней системой параллельных непрозрачных
полос, расположенных на одинаковых
расстояниях друг от друга.
Пусть на решетку (рис. 47) падает
монохроматический (определенной длины
волны) свет. В результате дифракции на
каждой щели свет распространяется не
только в первоначальном направлении,
но и по всем другим направлениям. Если
за решеткой поставить собирающую линзу,
то на экране в
фокальной плоскости все лучи будут
собираться в одну полоску.
Параллельные лучи, идущие от краев
соседних щелей, имеют разность хода I =
d sin ф, где d — постоянная решетки —
расстояние между соответствующими
краями соседних щелей, называемое
периодом решетки, ср — угол отклонения
световых лучей от перпендикуляра к
плоскости решетки. При разности хода,
равной целому числу длин волн , наблюдается
интерференционный максимум для данной
длины волны. Условие интерференционного
максимума выполняется для каждой длины
волны при своем значении дифракционного
угла ф. В результате при прохождении
через дифракционную решетку пучок
белого света разлагается в спектр. Угол
дифракции имеет наибольшее значение
для красного света, так как длина волны
красного света больше всех остальных
в области видимого света. Наименьшее
значение угла дифракции для фиолетового
света.
Опыт показывает, что интенсивность
светового пучка, проходящего через
некоторые кристаллы, например исландского
шпата, зависит от взаимной ориентации
двух кристаллов. При одинаковой ориентации
кристаллов свет проходит через второй
кристалл без ослабления.
Если же второй кристалл повернут на
90°, то свет через него не проходит.
Происходит явление поляризации, т. е.
кристалл пропускает только такие волны,
в которых колебания вектора напряженности
электрического поля совершаются в одной
плоскости — плоскости поляризации.
Явление поляризации доказывает волновую
природу света и поперечность световых
волн.
Узкий параллельный пучок белого света
при прохождении через стеклянную призму
разлагается на пучки света разного
цвета, при этом наибольшее отклонение
к основанию призмы имеют лучи фиолетового
цвета. Объясняется разложение белого
света тем, что белый свет состоит из
электромагнитных волн с разной длиной
волны, а показатель преломления света
зависит от длины его волны. Показатель
преломления связан со скоростью света
в среде, следовательно, скорость света
в среде зависит от длины волны. Это
явление и называют дисперсией
света.
На основании совпадения экспериментально
измеренного значения скорости
электромагнитных волн Максвелл высказал
предположение, что свет — это
электромагнитная волна. Эта гипотеза
подтверждена свойствами, которыми
обладает свет.
_20. Интерференция света. Оптическая разность хода, связь разности фаз с оптической разностью хода. Условия максимумов и минимумов интерференции. Интерференционная картина.
Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.
Разность хода лучей, разность
оптических
длин путей двух световых
лучей, имеющих общие начальную и конечную
точки. Понятие Р. х. играет основную роль
в описании интерференции
света и дифракции
света. Расчёты распределения
световой энергии в оптических
системах основаны на
вычислении Р. х. проходящих через них
лучей (или пучков лучей).
^
Оптическая разность хода.
Вместо
разности фаз
интерферирующих
волн удобно ввести в рассмотрение
пропорциональную ей величину
-
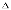оптическую разность хода, которая
отличается множителем
,
где
-
длина световой волны.
Изменению
разности фаз на
соответствует
изменение разности хода на
.
В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
ин
терпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода - это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.
Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:
.
В
изотропной среде скорость света в n раз
меньше, чем в вакууме, здесь n - показатель
преломления среды. Частота света в среде
и в вакууме одинакова, поэтому длина
волны в среде в n раз меньше. В соответствии
с соотношением
вместо
реального уменьшения длины волны
можно
рассматривать неизменную
и
соответствующее увеличение длины пути
луча. С этой целью вводится понятие
оптической длины пути, которая в n раз
больше геометрической длины. Далее,
употребляя термин "разность хода",
всегда будем иметь в виду оптическую
разность хода.
Заменяя разность
фаз интерферирующих волн оптической
разностью хода, получаем следующее
выражение для интенсивности
интерференционной картины:
.
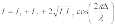Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.
Отметим, что разность
хода лучей можно отсчитывать не только
как разность длин путей от источника
до точки наблюдения, но и как разность
длин путей от двух точек любой поверхности
равной фазы волны до точки наблюдения.
При этом, конечно, две точки на поверхности
равной фазы - не произвольные точки, а
должны быть точками, через которые
реально проходят лучи, попадающие в
точку наблюдения. Так на рис. 18
,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
.
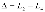Этот прием часто используется при
решении задач.
18.1.2.1. Условия
максимума и минимума на разность фаз
δ
Оптическая разность хода
Пусть
для простоты, начальные фазы α1
и α2 интерферирующих волн
равны нулю, тогда:
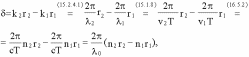здесь
λ0 = cT - длина световой
волны в вакууме.
Оптической
разностью хода называют величину:
.
Тогда:
.
^ 18.1.2.3. Условия максимума
и минимума на оптическую разность
хода
Из (18.1.2.1.) и (18.1.2.2.):
По
сле
сокращения получим условия на Δ:
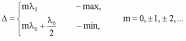
Получить устойчивую интерференционную
картину для света от двух разделённых
в пространстве и независящих друг от
друга источников света не так легко,
как для источников волн
на воде. Атомы испускают свет цугами
очень малой продолжительности, и
когерентность нарушается. Сравнительно
просто такую картину можно получить,
сделав так, чтобы интерферировали волны
одного и того же цуга. Так, интерференция
возникает при разделении первоначального
луча света на два луча при его прохождении
через тонкую плёнку, например плёнку,
наносимую на поверхность линз у
просветлённых
объективов.
Луч света, проходя через плёнку толщиной
,
отразится дважды — от внутренней и
наружной её поверхностей. Отражённые
лучи будут иметь постоянную разность
фаз, равную удвоенной толщине плёнки,
отчего лучи становятся когерентными и
будут интерферировать. Полное гашение
лучей произойдет при
,
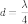где
—
длина
волны. Если
нм,
то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
—
условие максимума;
—
условие минимума,
где k=0,1,2… и
—
оптическая
длина пути первого и второго луча,
соответственно.
Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
_21. Понятие о когерентности световых волн. Сложение амплитуд двух когерентных световых волн с помощью векторной диаграммы. Интенсивность света при интерференции, условия максимумов и минимумов.
Интерференцию света можно объяснить, рассматривая интерференцию волн. Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Taк как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек.
Понять физическую причину немонохроматичности, а следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время ( 10–8с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени 10–8с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом.
Описанная модель испускания света справедлива и для любого макроскопического источника, так как атомы светящегося тела излучают свет также независимо друг от друга. Это означает, что начальные фазы соответствующих им волновых цугов не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы разных цугов отличаются для двух последующих актов излучения. Следовательно, свет, испускаемый макроскопическим источником, некогерентен.
Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга ког называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. ког < . Прибор обнаружит четкую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн.
Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течение времени когерентности ког. За это время волна распространяется в вакууме на расстояние lког =ског, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.
Чем ближе волна к монохроматической, тем меньше ширина спектра ее частот и, как можно показать, больше ее время когерентности ког, а следовательно, и длина когерентности lког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временнóй когерентностью.
Наряду с временнóй когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной пространственной когерентности) называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Таким образом, пространственная когерентность определяется радиусом когерентности. Радиус когерентности
где — длина волны света, — угловой размер источника. Так, минимально возможный радиус когерентности для солнечных лучей (при угловом размере Солнца на Земле 10–2 рад и 0,5 мкм) составляет 0,05 мм. При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза на расстоянии наилучшего зрения составляет лишь 0,1 мм. Отметим, что первое наблюдение интерференции провел в 1802 г. Т. Юнг именно с солнечным светом, для чего он предварительно пропускал солнечные лучи через очень малое отверстие в непрозрачном экране (при этом на несколько порядков уменьшался угловой размер источника света и тем самым резко увеличивался радиус когерентности (или длина пространственной когерентности)).
Пусть в некоторую точку пространства,
обычно называемую точкой наблюдения,
приходят от разных источников две
волны с одинаковой частотой
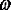и
с одинаковым направлением колебаний
электрических векторов
и
.
Тогда, согласно принципу суперпозиции,
результирующее колебание в точке P
будет иметь вид
,
причем
начальные фазы колебаний
и
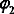будут
зависеть от координат источников и
точки наблюдения.
Для сложения колебаний применим метод
векторной диаграммы.
,
так
как
.
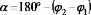Волны называются некогерентными, если
их разность фаз
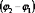зависит
от времени. Тогда среднее значение
быстропеременной гармонической функции
за время наблюдения
,
и среднее значение квадрата амплитуды
результирующего колебания
.
Интенсивность (или энергия) волны (а для
света - освещенность экрана) пропорциональна
квадрату ее амплитуды, т.е.
.
Поэтому
при наложении некогерентных волн их
интенсивности складываются, и
результирующая (усредненная) интенсивность
будет
одинакова во всех точках
пространства :
.
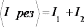Когерентными называются волны, для
которых разность фаз постоянна во
времени
.
В тех точках пространства (экрана), где
разность фаз когерентных волн равна
нечетному числу
,
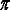т.е.
,
где m- целое число ( условие
минимума ), результирующая амплитуда
будет минимальной и равной
.
В
тех же точках, где разность фаз когерентных
волн равна четному числу , т.е.
,
где m- целое число (условие
максимума ), результирующая амплитуда
будет максимальной:
.
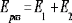Таким образом, при сложении когерентных
волн наблюдается интерференционная
картина, состоящая из устойчивых
максимумов и минимумов интенсивности
(освещенности) экрана.
Если амплитуды
интерферирующих волн одинаковы:
,
в точках минимума освещенность падает
до нуля, а в точках максимума
возрастает в четыре раза:
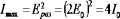
Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
|
|
(*) |
где Δ = r2 – r1 – так называемая разность хода.
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
_22. Примеры наблюдения интерференции света: интерференция в тонких пленках. Кольца Ньютона.
Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цугами. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, отчего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где — длина волны. Если нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей
— условие максимума;
— условие минимума,
где k=0,1,2… и — оптическая длина пути первого и второго луча, соответственно.
Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину.
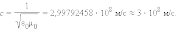
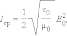
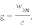
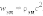