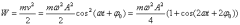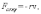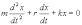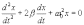Определения

• — угол отклонения маятника от равновесия;

• — начальный угол отклонения маятника;

• — масса маятника;

• — расстояние от точки подвеса до центра тяжести маятника;

• — радиус инерции относительно оси, проходящей через центр тяжести.

• — ускорение свободного падения.

Момент инерции относительно оси, проходящей через точку подвеса:

.

Уравнение динамики вращательного движения для физического маятника в проекции на ось вращения в случае его малых колебаний запишем в виде:

M_z = ·'' = - m·g·l·sin = - m·g·l·.

Решение этого уравнения имеет следующий вид:

(t) = _max·sin(w₀·t + ₀), где w₀ = (m·g·l/I)^1/2.

Для математического маятника момент инерции и значение собственной частоты колебаний будут равны: 

I = m·l² и  w₀ = (g/l)^1/2.

Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:

w₀ = (g/l_прив)^1/2,  где l_прив = I/(m·l) - приведенная длина маятника.

_3. Гармонические колебания: возвращающая сила и энергия колебаний. Необходимое условие гармонических колебаний.

При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

(Скорость тела v = ds/dt)

        Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

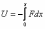
где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

        Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

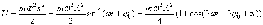
для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях: 2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника. 3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

        В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.

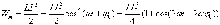
        Сравнивая эти формулы, можно сделать следующие выводы:

1. Полная энергия в контуре остается неизменной:

2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре. 3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.

        Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.

тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.  Такая сила называется квазиупругой.

На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:

|F(x)| = k·x + k₁·x² + k₂·x³ + ...

и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.

При максимальном отклонении грузика от положения равновесия вся энергия системы сосредоточена в потенциальной, и поэтому полная энергия колеблющейся системы может быть выражена через амплитуду колебаний и частоту:

E = kx_max²/2 = kA²/2 = mω²A²/2

Оказывается, этим свойстром обладают любые системы, колебание в которых происходит по гармоническому закону: энергия гармонического колебания (или волны) пропорциональна квадрату амплитуды этого колебания.

Единственным условием возникновения гармонических колебаний в рассмотренной системе оказалась линейная зависимость возвращающей силы от смещения. Такое условие выполняется при колебаниях многих (и не только механических) систем: это и малые колебания тела на длинной нерастяжимой нити в поле тяжести Земли (математический маятник), и колебания молекул, и электрические колебания в LC-контуре. Каждая из этих систем, обладающая свойством линейного возрастания возвращающей силы по мере удаления системы от положения равновесия, носит название линейного осциллятора (слово «осциллятор» происходит от латинского глагола, означающего «качаться»).

_4. Затухающие колебания: уравнение затухающих колебаний и его решение. Амплитуда, циклическая частота и период затухающих колебаний.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ

или

(7.18)

Перепишем это уравнение в следующем виде: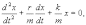

и обозначим:

где 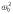представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение 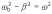тогда С вещественным ω решением этого уравнения, как мы знаем, является функция

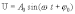
Таким образом, в случае малого сопротивления среды 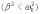, решением уравнения (7.19) будет функция

(7.20)

График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

_5. Основные характеристики затухающих колебаний: циклическая частота, период, коэффициент затухания, время затухания, логарифмический декремент затухания.

(см.4 вопрос).

_6. Логарифмический декремент затухания и добротность. Энергия при затухающих колебаниях. Формула для добротности через потери энергии.

Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:

Логарифмический декремент колебаний равен декременту, умноженному на период колебаний:

Добро́тность — свойство колебательной системы, определяющее полосу резонанса и показывающее, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

где:

•  — резонансная частота колебаний

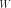•  — энергия, запасённая в колебательной системе

•  — рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.

Для последовательного Колебательного контура в RLC цепях, в котором все три элемента включены последовательно:

,

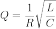где , и  — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.

Для параллельного контура, в котором индуктивность, емкость и сопротивление включены параллельно:

,

Для электрической цепи гораздо проще измерить амплитуду (ток или напряжение), чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды осцилляции, полоса на АЧХ будет от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой по уровню с круговой частотой резонанса :

,

где:  — коэффициент затухания, равный полуширине резонансной кривой, 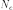 — число колебаний за время релаксации.

Рассмотрим процесс превращения энергии при гармоническом колебательном движении на примере идеального (F_тр=0) горизонтального пружинного маятника. Выводя тело из положения равновесия, например сжимая пружину на х=А, мы сообщаем ему некоторый запас потенциальной энергии  Wn0=kA22 (горизонтальный уровень, на котором находится маятник, выбираем за нулевой уровень отсчета потенциальной энергии маятника в поле силы тяжести, тогда W_п = 0). При движении тела к положению равновесия его потенциальная энергия Wn=kx22 убывает, а кинетическая Wk=mυ22 возрастает, так как деформация пружины уменьшается, а скорость движения тела увеличивается. В момент прохождения телом положения равновесия его потенциальная энергия равна нулю, а кинетическая Wk0=mυ2max2 — максимальна. После прохождения положения равновесия скорость тела уменьшается, а пружина растягивается. Следовательно, кинетическая энергия тела убывает, а потенциальная — возрастает. В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна. Таким образом, при колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно. Полная механическая энергия пружинного маятника равна сумме его кинетической и потенциальной энергий W=Wk+Wn.

Если смещение материальной точки, совершающей гармонические колебания, изменяется с течением времени по закону  x=Acosωt, то проекция скорости на ось х  υx=−ωAsinωt (см. § 13.2). Следовательно, кинетическая энергия в любой момент времени может быть задана функцией Wk=mυ22=mω2A2sin2ωt2=mω2A24(1−cos2ωt), а потенциальная энергия — функцией Wn=kx22=kA2cos2ωt2=mω2A24(1+cos2ωt), так как ω2=km, то  k=mω2.

Полная энергия W=mω2A2sin2ωt2+mω2A2cos2ωt2=mω2A22=kA22.

Из этих формул видно, что W_к и W_п изменяются тоже по гармоническому закону, с одинаковой амплитудой mω2A24 и в противофазе друг с другом и с частотой  2ω (рис. 13.13), а полная механическая энергия не изменяется со временем. в момент максимального Она равна либо потенциальной энергии тела отклонения, либо его кинетической энергии в момент прохождения положения равновесия:

W=kA22=mυ2m2=mω2A22.

Виды потерь и парциальные добротности. При расчете потерь в резонаторе приходится учитывать следующие факторы:

• потери в заполняющем диэлектрике – Р_Д;

• потери в металлических стенках резонатора – Р_М;

• потери на излучение (например, через отверстие в стенке) - Р ;

Очевидно, что мощность потерь Р_п = Р_Д + Р_М + Р . Для характеристики каждого вида потерь вводят парциальные добротности:

. (8.5)

Из (8.5) следует, что

.

8.3.4 Потери в диэлектрике. В большинстве случаев магнитные потери в заполняющей резонатор среде отсутствуют и необходимо учитывать только диэлектрические потери. Для расчета Р_Д воспользуемся выражением для средней мощности потерь гармонического поля из (5.11):

,(8.6)

где V – объем резонатора.

Энергию W определим как удвоенную среднюю энергию гармонического электрического поля:

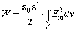.(8.7)

Подставив (8.5) и (8.7) в (8.5), получим выражение для парциальной добротности:

,

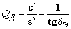где  _Э – угол диэлектрических потерь в заполняющей среде.

Если потери связаны только в наличием проводимости  в диэлектрике, то tg _Э= /  ₀  , т.е. Q_Д увеличивается с ростом резонансной частоты  .

8.3.5 Потери в стенках резонатора. Для определения парциальной добротности Q_М будем вычислять потери в стенках исходя из теории сильного скин-эффекта (5.12):

,

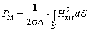где S – внутренняя поверхность всех стенок резонатора.

Электромагнитную энергию выразим через магнитное поле резонатора:

.

Подставляя Р_М и W в соответствующее выражение из (8.5), получим:

,(8.8)

где учтено, что толщина скин-слоя 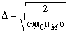. Обычно магнитные проницаемости диэлектрика и металла  _Д =  _М = 1.

Отношение интегралов в (8.8) при фиксированных форме резонатора и типе колебаний пропорционально линейному размеру резонатора, т.е. обратно пропорционально резонансной частоте. С учетом частотной зависимости  , мы получаем характер зависимости парциальной добротности от частоты: . С ростом резонансной частоты Q_М уменьшается.

Обычно потери в объемных резонаторах весьма малы, поэтому при расчете мощностей потерь в диэлектрике и металле можно в качестве приближения для поля реального резонатора использовать выражения для полей собственных частот (аналогично рассчитывалась погонная мощность потерь волновода в п. 5.4.1).

Вычисление парциальной добротности Q не сводится к применению некоторой общей формулы. В каждом конкретном случае, исходя из заданной формы, размеров и местоположения излучающего отверстия, ставится и решается численно-аналитическими методами граничная задача электродинамики. Резонатор и связанная с ним через отверстие структура рассматриваются как единая электродинамическая система.

 

_7. Вынужденные колебания, уравнение вынужденных колебаний. Амплитуда установившихся вынужденных колебаний. Сдвиг фаз между вынуждающей силой и смещением.

  ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы).

        Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.

        Рассмотрим вынужденные колебания на примере реального (с трением) пружинного маятника. Будем отталкиваться от уравнения движения (второй закон Ньютона), которое мы написали для затухающих колебаний. При наличии дополнительной вынуждающей силы F(t) необходимо дописать ее в правую часть уравнения. В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:

Для пружинного маятника:

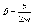     и    

        Для того, чтобы возникли периодические колебания, вынуждающая сила сама должна быть периодической. Пусть (писать здесь начальную фазу смысла нет, поскольку нас будут интересовать только установившиеся вынужденные колебания, то есть "забывшие" свое начало).  - частота вынуждающей силы. Для нахождения уравнения установившихся колебаний необходимо найти решение дифференциального уравнения:

     при     .

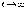        Общее решение этого неоднородного дифференциального уравнения представляет собой, как известно из теории дифференциальных уравнений, сумму общего решения однородного уравнения и любого частного решения неоднородного. Общее решение однородного уравнения нам известно, это - уравнение затухающих колебаний. Оно нас не интересует, так как при   оно исчезает. В качестве частного решения неоднородного уравнения выберем очевидное - мы знаем, что вынужденные установившиеся колебания совершаются с частотой вынуждающей силы. Поэтому нашим искомым решением будет являться:

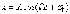
где А - амплитуда вынужденных колебаний, ۪  - сдвиг фаз между смещением и приложенной силой.

        Получившиеся колебания подчиняются закону синуса (или косинуса), то есть являются синусоидальными или гармоническими. Но это не свободные колебания в системе без трения; здесь вынуждающая сила постоянно поставляет энергию в систему, в точности компенсирующую потери на преодоление сил трения.

        Необходимо теперь найти амплитуду вынужденных колебаний и сдвиг фаз. Для этого необходимо подставить выражение для х в дифференциальное уравнение вынужденных колебаний. Обратите внимание, что необходимо найти два неизвестных из одного уравнения. Это возможно, если в процессе вычислений воспользоваться дополнительным (очевидным в процессе выкладок) условием. Попытайтесь проделать это.

Для амплитуды и сдвига фаз получаются следующие выражения:

здесь _- частота свободных (незатухающих) колебаний маятника;  - коэффициент затухания.

        Обратите внимание, что амплитуда вынужденных колебаний зависит от соотношения частоты вынуждающей силы и собственной частоты маятника. Максимальное значение амплитуды получается, если

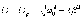
        Частота называется резонансной частотой, а достижение максимума амплитуды колебаний при изменении частоты называется явлением резонанса. График зависимости А() носит название резонансной кривой. Обратите внимание, что резонансная частота механических колебаний зависит от коэффициента затухания (а с ним и от коэффициента силы трения). Если силы трения отсутствуют, амплитуда колебаний стремится к бесконечности.

        Помимо поведения амплитуды при резонансной частоте рассмотрим ещё два предельных случая: 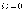и

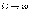
        В первом мы получим обычное статическое смещение маятника под действием постоянной силы F₀ (статическое растяжение пружины):

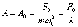
        Во втором случае амплитуда равна нулю: инерция маятника не может успевать реагировать на бесконечную частоту.

        Зависимость сдвига фаз от соотношения частот представлена на рисунке. Сдвиг фаз между смещением и вынуждающей силой обусловлен инерцией маятника.

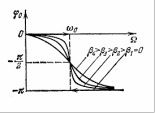
_8. Резонансная кривая при вынужденных колебаниях. Явление резонанса. Резонансная частота и резонансная амплитуда.

Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Исследуем зависимость амплитуды колебаний от частоты со вынуждающей силы. При малом затухании у эта зависимость имеет очень резкий характер. Если, то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом. При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Для нахождения частоты резонанса сорез, нужно найти, при каком со подкоренное выражение в формуле имеет минимум. Приравнивая производную этого выражения по со нулю или дополняя его до полного квадрата, убеждаемся, что максимум амплитуды вынужденных колебаний имеет место при Резонансная частота оказывается меньше частоты свободных колебаний системы. При малых у резонансная частота практически совпадает. При стремлении частоты вынуждающей силы к бесконечности при , амплитуда а, как видно, стремится к нулю при действии постоянной внешней силы. Это есть статическое смещение осциллятора из положения равновесия под действием постоянной силы.Максимальная амплитуда. Амплитуду вынужденных колебаний в резонансе находим, подставляя частоту из в выражение.Амплитуда колебаний в резонансе тем больше, чем меньше постоянная затухания. При изучении вынужденных колебаний вблизи резонанса трением пренебрегать нельзя, как бы мало оно ни было: только при учете затухания амплитуда в резонансе яре, получается конечной.Интересно сравнить значение со статическим смещением под действием силы. Составляя отношение, получаем при малом затуханииПодставляя сюда и учитывая, что есть время жизни собственных затухающих колебаний для той же системы в отсутствие внешних сил, находимНо есть число колебаний, совершаемых затухающим осциллятором за время жизни колебаний. Таким образом, резонансные свойства системы характеризуются тем же параметром, что и собственные затухающие колебания.Фазовые соотношения. Формула дает возможность проанализировать изменение сдвига фазы между внешней силой и смещением, при вынужденных колебаниях. При значение д близко к нулю. Это означает, что при низких частотах смещение осциллятора происходит в фазе с внешней силой. При медленном вращении кривошипа на рис. 178 маятник движется в такт с правым концом шатуна.Если стремится к нулю со стороны отрицательных значений,сдвиг фазы равен и смещение осциллятора происходит в противофазе с вынуждающей силой. В резонансе, как видно из, смещение отстает по фазе от внешней силы. Вторая из формул показывает, что при этом внешняя сила изменяется в фазе со скоростью все время действует в направлении движения. Что именно так и должно быть, ясно из интуитивных соображений.Резонанс скорости. Из формулы видно, что амплитуда колебаний скорости при установившихся вынужденных колебаниях равна. С помощью получаемЗависимость амплитуды скорости от частоты внешней силы показана на рис. 184. Резонансная кривая для скорости хотя и похожа на резонансную кривую для смещения, но отличается от нее в некоторых отношениях. Так, при при действии постоянной силы, осциллятор испытывает статическое смещение из положенияравновесия и скорость его после того, как закончится переходный процесс, равна нулю. Из формулы видно, что амплитуда скорости при обращается в нуль. Резонанс скорости имеет место при точном совпадении частоты внешней силы с частотой свободных колебаний.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет немонотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении частоты со вынуждающей силы к собственной частоте со0 осциллятора называется резонансом.Формула дает выражение для амплитуды вынужденных колебаний в пренебрежении трением. Именно с этим пренебрежением связано обращение амплитуды колебаний в бесконечность при точном совпадении частот. Реально амплитуда колебаний в бесконечность, конечно же, обращаться не может.Это означает, что при описании вынужденных колебаний вблизи резонанса учет трения принципиально необходим. При учете трения амплитуда вынужденных колебаний при резонансе получается конечной. Она будет тем меньше, чем больше трение в системе. Вдали от резонанса формулой можно пользоваться для нахождения амплитуды колебаний и при наличии трения, если оно не слишком сильное. Более того, эта формула, полученная без учета трения, имеет физический смысл только тогда, когда трение все же есть. Дело в том, что само понятие установившихся вынужденных колебаний применимо только к системам, в которых есть трение.

Если бы трения совсем не было, то процесс установления колебаний продолжался бы бесконечно долго. Реально это означает, что полученное без учета трения выражение для амплитуды вынужденных колебаний будет правильно описывать колебания в системе только спустя достаточно большой промежуток времени после начала действия вынуждающей силы. Слова «достаточно большой промежуток времени» означают здесь, что уже закончился переходный процесс, длительность которого совпадает с характерным временем затухания собственных колебаний в системе. При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при со и в противофазе при, как и в отсутствие трения. Однако вблизи резонанса фаза меняется не скачком, а непрерывно, причем при точном совпадении частот смещение отстает по фазе от вынуждающей силы на (на четверть периода). Скорость изменяется при этом в фазе с вынуждающей силой, что обеспечивает наиболее благоприятные условия для передачи энергии от источника внешней вынуждающей силы к осциллятору.

Будем рассматривать зависимость амплитуды А вынужденных колебаний от частоты ω. Будем рассматривать механические и электромагнитные колебания одновременно, при этом называя колеблющуюся величину либо смещением (х) тела, испытавающего колебания, из положения равновесия, либо зарядом (Q) конденсатора. Из формулы (8) предыдущего раздела следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту ω_rez , — частоту, при которой амплитуда А смещения (заряда) будет максимальна, — нужно найти максимум функции (8) предыдущего раздела, или, что равносильно, минимум подкоренного выражения. Продифференцировав выражение под корнем по ω и приравняв его нулю, получим условие, из которого найдем ω_rez : Это равенство верно при 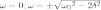, у которых только выражение со знаком плюс имеет физический смысл. Значит, резонансная частота (1) Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При ω₀² >> δ² значение ω_rez практически равно собственной частотой ω₀ колебательной системы. Подставляя (1) в формулу (8) предыдущего раздела, найдем 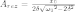(2)

Из формулы (2) следует, что при малом затухании (ω₀² >> δ²) резонансная амплитуда смещения (заряда) где Q — добротность колебательной системы, x₀/ω₀² - рассмотренное выше статическое отклонение. Значит, добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А_rez. На рис. 2 даны резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока) достигает максимального значения при ω_rez=ω₀ и равна x₀/(2δ) , т. е. чем больше коэффициент затухания δ , тем ниже максимум резонансной кривой. Применяя выражения для циклического частоты свободных колебаний пружинного маятника, формулы δ=r/(2m) и и выражение для циклической частоты свободно колеблющегося колебательного контура вместе с δ=r/(2m), получим, что амплитуда скорости при механическом резонансе равна а амплитуда тока при электрическом резонансе будет Из выражения tgφ = 2δω/(ω₀² - ω²) вытекает, что если в системе отсутствует затухание (δ=0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях φ≠0.

_9. Колебательный контур. Уравнение колебаний в контуре. Период и частота колебаний, коэффициент затухания, добротность колебательного контура.

КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных незатухающих колебаний

, где w₀ = - СОБСТВЕННАЯ ЧАСТОТА контура .

ПЕРИОД Т = 2p .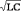

Его решение q(t) = q_v cos(w₀ t + a), где a - начальная фаза.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний

, где b = 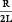- коэффициент затухания.

Его решение q(t) = q_v0 е^-bt cos(wt + a), где - частота затухающих колебаний..

ПОСТОЯННАЯ ВРЕМЕНИ ЗАТУХАНИЯ в контуре t есть время, за которое амплитуда колебаний уменьшается в е = 2.73 раз. На графике зависимости амплитуды затухающих колебаний от времени касательная, проведенная к этому графику в начальный момент времени, пересекает ось времени в точке t = t.

ЛОГАРИФМИЧЕСКИМ ДЕКРЕМЕНТНОМ ЗАТУХАНИЯ называется величина, определяемая формулой 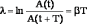. ДОБРОТНОСТЬ контура равна Q = .

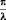_10. Сложение колебаний происходящих в одном направлении с помощью векторной диаграммы.

Пусть складывается два колебания:

строим векторные диаграммы и складываем векторы:

По теореме косинусов .

Так как

,

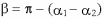то

.

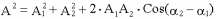начальная фаза результирующего колебания определяется соотношением:

.

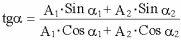Волны

_11. Волновые процессы, классификация волн. Уравнение плоской волны.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и попереч­ные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.

Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением  частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции (x, t) похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы от времени.

Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны  (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.

или, учитывая, что T= 1/, где  — частота колебаний,

Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени — один. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.

уpавнение плоской волны без диспеpсии имеет следующий вид:

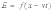или

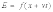
Здесь v есть фазовая скоpость волны, а вид функции f может быть любым.

_12. Уравнение плоской волны. Основные характеристики волн: частота, фазовая скорость, длина волны и волновой вектор.

уpавнение плоской волны без диспеpсии имеет следующий вид:

или

Здесь v есть фазовая скоpость волны, а вид функции f может быть любым.

Частота Волны - ЧАСТОТА ВОЛНЫ, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в ГЕРЦАХ. Ее можно вычислить, разделив скорость распространения волны на длину волны. Согласно КВАНТОВОЙ ТЕОРИИ, частота любого ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ (включая свет, радиоволны, рентгеновское излучение) пропорциональна энергии составляющих его фотонов. Многие характеристики электромагнитного излучения зависят от частоты.

Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Ее можно рассматривать при желании как векторную величину.

Основная формула, определяющая фазовую скорость (монохроматической) волны в одномерном пространстве или фазовую скорость вдоль волнового вектора для волны в пространстве большей размерности:

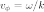
которая является прямым следствием того факта, что фаза плоской волны в однородной среде есть

для одномерного случая

или для размерности, большей единицы.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой . По аналогии с волнами, возникающими в воде от брошенного камня, длиной волны является расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина 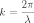, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Получить соотношение, связывающее длину волны с фазовой скоростью ( ) и частотой ( ) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний , поэтому

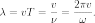
Для определения длины волны электромагнитного излучения в какой-либо среде следует использовать формулу:

где — показатель преломления среды для излучения с данной частотой.

Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:

• частота:

• длина волны:

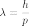
где h — постоянная Планка.

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.

Волновой вектор обычно обозначается латинской буквой и величина его измеряется в обратных метрах (СИ) или обратных сантиметрах (СГС) (т.е. радианах на метр или радианах на сантиметр). Следует быть внимательным, т.к. иногда может использоваться определение в оборотах, отличающееся множителем , но дающее ту же физическую размерность.

Волновое число связано с длиной волны λ соотношением:

.

Связь между волновым вектором и частотой задаётся законом дисперсии. Все возможные значения волновых векторов образуют обратное пространство или k-пространство.

Наиболее общим определением волнового вектора можно считать такое: волновой вектор есть градиент фазы волны:

_13. Фаза волны и волновые поверхности. Фазовая скорость упругой волны и её физический смысл. Формулы для фазовой скорости волн в различных средах.

Под фазой понимается состояние волны в данной точке и в данный момент вpемени, описанное соответствующими паpаметpами. Напpимеp, фаза электpомагнитной волны задается модулями вектоpов Е и В. Фаза от точки к точке меняется. Таким обpазом, фаза волны в математическом смысле есть функция кооpдинат и вpемени. С понятием фазы связано понятие волновой повеpхности. Это повеpхность, все точки котоpой в данный момент вpемени находятся в одной и той же фазе, т.е. это повеpхность постоянной фазы.

В жидкостях и газах, к-рые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения-сжатия, где колебания частиц среды происходят в направлении распространения волны. Фазовая скорость их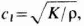 где К-модуль всестороннего сжатия, р - плотность среды. Пример таких У. в.- звуковые волны.

В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в. только двух типов - продольные и сдвиговые. В продольных У. в. движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. В безграничной среде распространяются продольные и сдвиговые волны трёх типов - плоские, сферические и цилиндрические. Их особенность - независимость фазовой и групповой скоростей от амплитуды и геометрии волны. Фазовая скорость продольных волн в неограниченной твёрдой среде 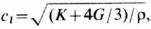сдвиговых волн- (G - модуль сдвига). Величины с_i и c_t для разных сред колеблются в пределах от сотен до неск. тысяч м/с.

На границе твёрдого полупространства с вакуумом, газом, жидкостью или с др. твёрдым полупространством могут распространяться упругие поверхностные волны (см. Поверхностные акустические волны ),являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды к-рых экспоненциально убывают при удалении от границы.

В ограниченных твёрдых телах (пластина, стержень), представляющих собой твёрдые волноводы акустические, могут распространяться только нормальные волны ,каждая из к-рых является комбинацией неск. продольных и сдвиговых волн, распространяющихся под острыми углами к оси волновода и удовлетворяющих граничным условиям: отсутствию механич. напряжений на поверхности волновода. Число п нормальных волн в пластине или стержне определяется толщиной или диаметром d, частотой w и модулями упругости среды. При увеличении число нормальных волн возрастает, и при . Нормальные волны характеризуются дисперсией фазовой и групповой скоростей.

_14. Энергетические характеристики волн, вектор Умова. Амплитуда сферической волны. Поглощение волн в среде.

a) Плотность потока энергии (количество энергии, переносимое волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны):

S(t) = W0(t)V.  (7.9)

б) Интенсивность волны (среднее по времени значение плотности потока энергии):

I = <S(t)> = <W0(t)>V. (7.10)

При усреднении по времени плотности энергии волны учтем, что среднее по времени значение квадрата гармонической функции равно 1/2, поэтому, например, для электромагнитной волны – см. (7.8):

 I = E0B0/20,  (7.10,a)

где E0 и B0 – амплитудные значения напряженности электрического и индукции магнитного полей, соответственно.

  в) Векторы Умова (для упругих волн) и Пойнтинга (для электромагнитных волн):

  S(t) = W0(t)V. (7.11)

В частности, вектор Пойнтинга можно записать в виде:

 S(t) = [EB]/0.  (7.11,a)

 г) Средние по времени значения векторов Умова и Пойнтинга («векторная интенсивность»):

<S(t)> = <W0(t)>V.  (7.12)

В частности, для электромагнитной волны

<S(t)> = [E0B0]/20.  (7.12,а)

д) Поток энергии волны через некоторую поверхность s и среднее по времени значение этого потока:

Ф(t) =  = 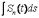,  (7.13)

<Ф(t)> =  = . (7.14)

Здесь ds – вектор, модуль которого равен элементарной площадке ds, а направление совпадает с направлением нормали к этой площадке; Sn – нормальная к площадке ds составляющая вектора S.

Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846—1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

При наличии поглощения в среде энергия С. в. убывает в направлении её распространения. Для гармонии. С. в. поглощение может быть учтено заменой k на k' + k'', где k'' - мнимая часть волнового числа. Это означает, что амплитуда волны затухает по экспоненте:

Существуют и несимметричные С. в., амплитуды к-рых зависят от полярной q и азимутальной j угл. координат, но фазовые фронты по-прежнему остаются сферическими:

где U(r, t)отвечает симметричной С. в., напр. в форме (1) или (2), a D(q, j) описывает угл. зависимость поля (эту ф-цию можно представить в виде суперпозиции т. н. сферич. гармоник). В однородных изотропных средах волновое поле на больших расстояниях от центра почти всегда имеет вид (3). Подбором D можно концентрировать поле около заданных направлений, поэтому ф-ция D(q, j) наз. диаграммой направленности излучения источника.

ПОГЛОЩЕНИЕ ВОЛН - превращение энергии волны в др. виды энергии в результате её взаимодействия с др. волнами или со средой, в к-рой она распространяется, или с телами, к-рые расположены на пути её распространения. В зависимости от природы волн и свойств среды механизм П. в. может быть различным (напр., при поглощении звука и поглощении света), но во всех случаях П. в. приводит к ослаблению интенсивности волны. Ослабление волн при распространении может быть вызвано не только собственно поглощением, но и др. явлениями, при к-рых энергия падающей волны переходит в энергию др. типов волн, возникающих под действием падающей волны (напр., при рассеянии волн)

_15. Образование стоячей волны как результат сложения прямой и отраженной волн. Узлы и пучности стоячей волны. Граничные условия для закрепленной струны, собственные частоты струны.

Рассмотрим образование стоячей волны в результате сложения падающей и отраженной волн, их можно наглядно показать на веревке. Если резко качнуть незакрепленный конец веревки, то вдоль нее побежит волна. Дойдя до конца веревки, она отразится, и в обратном направлении побежит отраженная волна. Если непрерывно качать веревку, то движения прямой и отраженной волн заметить уже нельзя. На веревке образуются узлы, в которых она неподвижна, и пучности, в которых амплитуда ее колебаний максимальна. Узлы и пучности по веревке не перемещаются. Стоячая волна в разомкнутой линии. Отражение волн тока и напряжения в разомкнутой линии происходит следующим образом. При распространении волны тока вдоль линии по ее проводам перемещаются электрические заряды. Заряды, дошедшие до конца линии, не могут дальше двигаться, на мгновение останавливаются и начинают двигаться в обратном направлении. Так как в самом конце линии движения электрических зарядов быть не может, то ток в этом месте линии всегда равен нулю, т. е. на конце линии образуется узел тока. Вследствие того что заряды на конце линии на мгновение останавливаются, там происходит скопление электрических зарядов и напряжение повышается. Поэтому в конце линии всегда образуется пучность напряжения. Итак, на разомкнутом конце линии всегда образуются узел тока и пучность напряжения. Так как узлы и пучности чередуются между собой через каждые четверть волны, то на расстоянии от конца линии будут пучность тока и узел напряжения, на некотором расстоянии - снова узел тока и пучность напряжения и т. д.

Пучность — участок стоячей волны, в котором колебания имеют наибольшую амплитуду. Противоположностью пучности является узел — участок волны, в котором амплитуда колебаний минимальна.

В натянутой струне, закрепленной с обоих концов, при возбуждении какого-либо произвольного поперечного возмущения возникнет довольно сложное нестационарное движение. Стационарное же движение в виде стоячей волны возможно лишь при вполне определенных частотах. Это связано с тем, что на закрепленных концах струны должны выполняться определенные граничные условия: в них смещение u все время должно равняться нулю. Значит, если в струне возбуждается стоячая волна, то концы струны должны быть ее узлами. Отсюда следует, что на длине струны  должно укладываться целое число п полуволн:  = n∙λ/2.

Найдем собственные частоты стержня, закрепленного на одном конце, если длина стержня , модуль Юнга материала стержня E и его плотность ρ.

Поскольку свободный конец стержня должен быть пучностью, на длине стержня установится целое число полуволн и еще четверть волны, т. е.  = nλ/2 + λ/4 = (2n + 1)λ/4. Отсюда найдем возможные значения λ_n, а затем, учитывая (1.26), и собственные частоты:

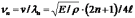,    n=0,1,2.

_16. Уравнения бегущей и стоячей волны. Сравнительная характеристика бегущей и стоячей волн.

Если колебания точек, лежащих в плоскости х=0, описываются функцией (0, t) = A cos t, то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на , так как для прохождения волной расстояния х требуется время  = x/v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид

                                                         (154.1)

откуда следует, что (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

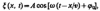                                     (154.2)

где А = const — амплитуда волны,  — циклическая частота, ₀ — начальная фаза вол­ны, определяемая в общем случае выбором начал отсчета х и t, [ (t—x/v)+ ₀] — фаза плоской волны.

Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны:

Преобразовав это уравнение, получим упрощенное уравнение стоячей волны:

В отличие от бегущих волн, стоячие волны не переносят энергии, а точки колеблющейся системы (тела, среды) находятся в одинаковой фазе колебания, но с разными амплитудами. Образующиеся пучности и узлы разделены расстоянием, равным 1/2 длине волны.

_17. Электромагнитные волны и их свойства.

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве. Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Электромагнитные волны возникают всегда, когда в пространстве есть изменяющееся электрическое поле. Такое изменяющееся электрическое поле вызвано, чаще всего, перемещением заряженных частиц, и как частный случай такого перемещения, переменным электрическим током.