ФИЗИКА 2013
ВОПРОСЫ к ЭКЗАМЕНУ
Семестр 2
Колебания
_1. Гармонические колебания: уравнение гармонических колебаний и его решение. Амплитуда, период и частота колебаний. Математический и физический маятники.
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
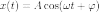где х — смещение (отклонение)
колеблющейся точки от положения
равновесия в момент времени t; А —
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия; ω — циклическая
частота, величина, показывающая число
полных колебаний происходящих в течение
2π секунд;
—
полная фаза колебаний,
—
начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
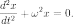
(Любое нетривиальное решение этого
дифференциального уравнения — есть
гармоническое колебание с циклической
частотой
)
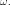Дифференциальное уравнение колебательного движения
Для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения
.
Решение дифференциального уравнения
Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество.
Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид:
,
т.е. является гармонической функцией. Значит уравнение , это дифференциальное уравнение гармонических колебаний.
Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.
Иначе: Амплитуда — модуль максимального отклонения тела от положения равновесия. Например:
амплитуда для механического колебания тела (вибрация), для волн на струне или пружине — это расстояние и записывается в единицах длины;
амплитуда звуковых волн и аудиосигналов обычно относится к амплитуде давления воздуха в волне, но иногда описывается как амплитуда смещения относительно равновесия (воздуха или диафрагмы говорящего). Её логарифм обычно измеряется в децибелах (дБ);
для электромагнитного излучения амплитуда соответствует величине напряженности электрического и магнитного поля.
Форма изменения амплитуды называется огибающей волной.
Частота |
|
|
|
Размерность |
T−1 |
Единицы измерения |
|
СИ |
Гц |
Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Стандартные обозначения в формулах — ν, f, ω или F. Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz), названный в честь немецкого физика Генриха Герца.
Величина, обратная частоте, называется периодом: T = 1/f.
Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором он находился в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея ввиду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно - с тем или иным успехом - и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное
обозначение периода колебаний:
(хотя
могут применяться и другие, наиболее
часто это
,
иногда
и
т. д.).
Единицы измерения: секунда
Период колебаний связан соотношением взаимной обратности с частотой:
Для волновых процессов период связан
кроме того очевидным образом с длиной
волны
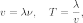
где
-
скорость распространения волны (точнее
- фазовая
скорость).
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
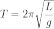
и не зависит от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Физический маятник — Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести.