
- •Рух тіла по колу
- •1. Рівномірний рух по колу
- •2. Період обертання і обертова частота
- •1. Елементарна формула
- •2. Мотивування та висновок
- •2.1. Геометричний висновок для нерівномірного руху по колу
- •2.2. Геометричний висновок для довільного руху (по довільній траєкторії)
- •2.3. Формальний висновок
- •3. Зауваження
- •4. Історія
Доцентрове прискорення - прискорення при рівномірному русі матеріальної точки по колу. Доцентрове прискорення є векторною величиною. Вектор доцентрового прискорення завжди направлений від матеріальної точки до центра кола.
Доцентрове прискорення показує не зміну модуля швидкості (як при прямолінійному русі), а зміну напряму швидкості.
Модуль доцентрового прискорення визначається формулою
![]() ,
,
де v - модуль швидкості матеріальної точки, R - радіус кола.
Доцентрове прискорення є частковим випадком нормального прискорення, яке виникає при будь-якому криволінійному русі.
Рух тіла по колу
У природі та техніці дуже часто зустрічається криволінійний рух. Він складніший за прямолінійний, тому що існує безліч криволінійних траєкторій; цей рух завжди прискорений, навіть коли модуль швидкості не змінюється. Але рух по будь-якій криволінійній траєкторії можна приблизно уявити як рух по дугах кола.
При русі тіла по колу напрямок вектора швидкості змінюється від точки до точки. Тому коли кажуть про швидкість такого руху, мають на увазі миттєву швидкість. Вектор швидкості спрямовано по дотичній до кола, а вектор переміщення — по хордах.
Рівномірний рух по колу — це рух, під час якого модуль швидкості руху не змінюється, змінюється тільки її напрямок. Прискорення такого руху завжди спрямоване до центру кола і називається доцентровим. Для того щоб знайти прискорення тіла, яке рухається по колу, необхідно квадрат швидкості поділити на радіус кола.
Крім прискорення, рух тіла по колу характеризують такі величини:
Період обертання тіла — це час, за який тіло робить один повний оберт. Період обертання позначається літерою Т та вимірюється в секундах.
Частота обертання тіла — це число обертів за одиницю часу. Частота обертання позначається літерою ν та вимірюється в герцах. Для того щоб знайти частоту, треба одиницю поділити на період.
Лінійна швидкість — відношення переміщення тіла до часу. Для того щоб знайти лінійну швидкість тіла по колу, необхідно довжину кола поділити на період (довжина кола дорівнює 2π помножити на радіус).
Кутова швидкість — фізична величина, яка дорівнює відношенню кута повороту радіуса кола, по якому рухається тіло, до часу руху. Кутова швидкість позначається літерою ω та вимірюється в радіанах, поділених на секунду. Знайти кутову швидкість можна, поділивши 2π на період. Кутова швидкість і лінійна між собою пов’язані. Для того щоб знайти лінійну швидкість, необхідно кутову швидкість помножити на радіус кола.
1. Рівномірний рух по колу
Увагу учнів слід звернути на те, що криволінійні рухи більш поширені, ніж прямолінійні. Будь-який криволінійний рух можна розглядати як рух по дугах кіл з різними радіусами. Вивчення руху по колу дає також ключ до розгляду довільного криволінійного руху.
Ми будемо вивчати рух тіл по колу з постійною за модулем швидкістю. Такий рух називають рівномірним рухом по колу.
Спостереження показують, що маленькі частинки, що відокремлюються від тіла, що обертається, летять із тією швидкістю, якою володіли в момент відриву: бруд з-під коліс автомобіля летить по дотичній до поверхні коліс; розпечені частинки металу, що відриваються при заточенні різця об точильний камінь, що обертається, також летять по дотичній до поверхні каменя.
Таким чином,
Під час руху по колу швидкість у будь-якій точці траєкторії спрямована по дотичній до кола в цій точці.
Необхідно звернути увагу учнів, що при рівномірному русі по колу модуль швидкості тіла залишається постійним, але напрямок швидкості увесь час змінюється.
2. Період обертання і обертова частота
Рух тіла по колу часто характеризують не швидкістю руху, а проміжком часу, за який тіло робить один повний оберт. Ця величина називається періодом обертання.
Період обертання — це фізична величина, що дорівнює проміжку часу, за який тіло, що рівномірно обертається, робить один оберт.
Період обертання позначається символом T. Наприклад, Земля робить повний оберт навколо Сонця за 365,25 діб.
При розрахунках період звичайно виражають у секундах. Якщо період обертання дорівнює 1с, це означає, що тіло за одну секунду робить один повний оберт. Якщо за час t тіло зробило N повних обертів, то період можна визначити за формулою:
Якщо відомий період обертання Т, то можна знайти швидкість тіла v. За час t, що дорівнює періоду Т, тіло проходить шлях, що дорівнює довжині кола: . Отже,
Рух тіла по колу можна характеризувати ще однією величиною — числом обертів по колу за одиницю часу. Її називають обертовою частотою:
обертова частота дорівнює кількості повних обертів за одну секунду.
Обертова частота й період обертання зв’язані таким співвідношенням:
Частоту в СІ вимірюють в
І. Організаційний момент.
Оголошення теми і мети уроку.
. Прискорення прямолінійного рівнозмінного руху можна визначити за формулою
 2.
Середня скалярна швидкість рівнозмінного
руху
2.
Середня скалярна швидкість рівнозмінного
руху

3. Шлях прямолінійного рівнозмінного (рівноприскореного) руху:

4. Якщо тіло рухається рівноприскорено без початкової швидкості , то пройдений шлях:

5. Проекцію переміщення під час рівноприскореного руху знаходимо:

6. Рівняння рівнозмінного прямолінійного руху:
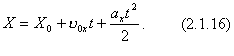
7.
![]()
8. Якщо прямолінійний рівноприскорений рух тіла починається зі стану спокою:
![]()
![]()
9. Якщо падаючому тілу надати початкову швидкість, напрямлену вниз, то формули кінематичних величин у проекціях на вісь, напрямлену вниз, мають вигляд:
υ
= υ + gt; h = υ
t
+
+ gt; h = υ
t
+
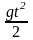 ;
h
=
;
h
=
 .
.
10. Для вільного падіння з висоти h без початкової швидкості, коли координатна вісь напрямлена вниз, формули мають вигляд:
υ
= gt; h =
;
h
=
 .
.
11. Рух тіла, кинутого вертикально вгору:
υ = υ - gt; h = υ t - ; h = - ; y = y + υ t - ;
Максимальна висота підйому тіла та час його руху:
h
=
 .
.
12.
Коли тіло падає без початкової швидкості
з висоти h
за час t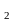 :
:
h
=
 ,
звідки t
=
,
звідки t
=
 ,
або t
=
,
або t
=
 .
.
ІІІ. Вивчення нового матеріалу.
Рух тіла по колу зі сталою швидкістю умовно називають рівномірним рухом по колу.
При рівномірному русі тіла по колу його прискорення у будь-якій точці траєкторії напрямлене по радіусу до центра кола. Це прискорення називають доцентровим.
Лінійна швидкість, v (м/с).
Кутова швидкість, (рад/с).
Доцентрове прискорення, а (м/с²).
Період обертання, Т (с).
Частота обертання, (рад/с).
 Лінійне
і кутове переміщення
Лінійне
і кутове переміщення
при русі тіла по колу.


Доцентрове прискорення тіла
Напрямлено по радіусу до центру кола.

При нерівномірному русі тіла:

Тангенціальне прискорення тіла:

Для русі тіла по колу необхідно, щоб на це тіло діяла сила, напрямлена до центру кола і дорівнювала:
F=mv²/r или F=m²r.
Періодом обертання називається проміжок часу, за який тіло робить один повний оберт.
Частотою обертання називають величину, що дорівнює кількості обертів за одиницю часу.
T
=
 ;
ν
=
;
ν
=
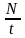 ;
ν
=
;
ν
=
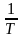 ;
υ
=
;
υ
=
 ;
T
=
;
T
=
 .
.
Доцентрове прискорення - компонента прискорення точки, що характеризує зміну напряму вектора швидкості для траєкторії з кривизною. (Друга компонента,тангенціальне прискорення, характеризує зміною модуля швидкості.) Направлено до центру кривизни траєкторії, чим і обумовлений термін. За величиною дорівнює квадрату швидкості, поділеному на радіус кривизни. Термін "доцентрове прискорення" в цілому еквівалентний терміну "нормальне прискорення";відмінності лише стилістичні (іноді історичні).
Найбільш простим прикладом доцентровий прискорення є вектор прискорення при рівномірному русі по колу (спрямований до центру кола).
В класичній механіці доцентрове прискорення викликається компонентами сил, спрямованими ортогонально вектору швидкості (і отже - перпендикулярно дотичній до траєкторії в даній точці). Наприклад, кривизна орбіт космічних об'єктів характеризується доцентровим прискоренням, викликаним гравітацією.
Пов'язане поняття для неінерційній систем відліку - відцентрова сила.
