1.4 Фильтры Калмана на основе «unscented» и «spherical-radial cubature» преобразований
Использование сильно нелинейных моделей динамики и/или наблюдения системы приводит к плохой численной обусловленности задачи фильтрации, то есть малая погрешность задания параметров математической модели будет приводить к большим вычислительным ошибкам. В результате алгоритм утратит робастность (устойчивость к погрешностям). В таких случаях применяют более точный, чем основанный на линейных членах ряда Тейлора, метод гауссовой аппроксимации апостериорной условной ПРВ (3) и (4).
Метод
называется Unscented
Transform
(UT),
соответствующий фильтр ‒
Unscented
Kalman
Filter
(UKF),
разработан и опубликован [15] в оксфордском
университете в 1995 году. Данная методика
подразумевает выбор специальным методом
набора характерных точек («sigma-points»)
в пространстве параметров состояния,
который с достаточной точностью
характеризует статистические
характеристики (моменты различных
порядков) искомого случайного вектора
параметров
размерности 
[15], [16], [17], [18]. Для выбора 
характерных точек, симметрично
расположенных относительно среднего,
используются выражения вида:
(46)
, 
(47)
, 
(48)
с
соответствующими весовыми коэффициентами
для каждой 
-й
точки:
(49)
(50)
, 
(51)
где
‒
-й
столбец матричного квадратного корня.
Следует обратить внимание, на то, что
вес для вычисления среднего 
и вес для вычисления ковариационной
матрицы 
в нулевой компоненте (
),
различны, для компенсации масштабирования
в пространстве параметров. 
‒
масштабный коэффициент, определяется
как 
.
,
,
‒
константные параметры «unscented»
преобразования.
определяет меру разброса точек вокруг
,
обычно берется небольшая положительная
величина из диапазона 
.
Константа
берется равной нулю или 
для случая гауссовой априорной ПРВ.
используется для ввода априорных знаний
о характере ПРВ
,
для нормальной ПРВ 
[ ]. Выражения (46)
‒
(51) однозначно характеризуют статистику
лишь для первого и второго моментов
распределения. Преобразования,
аппроксимирующие ПРВ до моментов более
высоких порядков (например, коэффициент
асимметрии и коэффициент эксцесса),
отличаются количеством характерных
точек и способом выбора весов [11], [40].
Фильтр Калмана на основе «Spherical-Radial Cubature» преобразования [19], [20] (Cubature Kalman filter (CKF)) разработан канадскими специалистами в 2009 году для системы с когнитивным радиолокационным сопровождением [19].
Обойдя
должным вниманием вопросы вывода
«spherical-radial
cubature»
преобразования, сделаем заключение о
том, что CKF
эквивалентен
частному случаю значений параметров
преобразования в UKF
(
,
,
)
[19]. Однако, имеет на одну характерную
точку меньше, что позволяет снизить
количество вычислений при практически
той же точности оценки. CKF
удаляет среднюю точку (
),
остается 
векторов с одинаковыми весами 
.
Основная идея рассмотренных преобразований в интуитивном предположении заключается в том, что намного легче аппроксимировать функцию ПРВ случайной величины с ненулевым средним (коей и является вектор состояния ‒ на него спроецирована случайная помеха ), чем аппроксимировать некую произвольную нелинейную функцию преобразования. Этот метод устраняет необходимость явного вычисления частных производных для матрицы Якоби, что само по себе является трудной задачей для сложных нелинейных функций. Cостояние системы экстраполируется и наблюдается без вычисления линеаризованных матричных операторов перехода и наблюдения . Таким образом, метод снимает ограничение на дифференцируемость функций.
Алгоритм
UKF
начинает свою работу с того, что
векторов 
преобразовываются известной нелинейной
функцией перехода состояния системы
:
,
(52)
Из результата преобразования путем взвешенного суммирования находятся итоговые оценки вектора математического ожидания и ковариационной матрицы экстраполированного состояния системы:
(53)
(54)
Далее точек, полученных в (52), пропускаются через нелинейную векторную функцию наблюдения :
(55)
Объединенная оценка вектора математического ожидания и ковариационной матрицы экстраполированного наблюдения:
(56)
(57)
Таким образом формируется гауссова аппроксимация ПРВ вида (3). Выражения (54) и (57) справедливы, только в условиях БГШ динамики и наблюдения.
Наличие нескольких точек, статистически характеризующих один и тот же вектор, приводит к альтернативному способу получения матрицы взаимной ковариации экстраполированного состояния и измерения:
(58)
Для алгоритма CKF выражения (52) ‒ (57) отличаются только количеством компонент ( ).
Затем рассчитывается матричный коэффициент усиления , обновленный вектор и ковариационная матрица состояния, путем подстановки (53), (54), (56), (57) в стандартные выражения для линейного ФК (13) ‒ (15):
(59)
(60)
(61)
Выражения (46) ‒ (61) составляют один цикл работы алгоритма UKF. Самой ресурсоемкой процедурой является вычисление матричного квадратного корня при формировании набора характерных точек.
По сравнению с РФК, главными преимуществами UKF и CKF являются: большая робастность, общность синтеза для разных нелинейных функций, обладают сравнимой с РФК вычислительной сложностью [41]. При этом часто позволяют получить более точные оценки, поскольку реализуют, по существу, не аналитическую, а статистическую линеаризацию нелинейностей, численная обусловленность такой процедуры выше. Кроме того, в алгоритме предлагается альтернативный решению матричного уравнения Риккати (17), способ вычисления оптимального коэффициента усиления ФК.
Возможно модифицировать алгоритм UKF путем формирования расширенного состояния системы, объединяющего параметры состояния и параметры шума [40], дополнив вектор состояния, средними значений шума динамики и наблюдения, а ковариационную матрицу состояния ‒ дисперсиями и взаимными дисперсиями шумовых последовательностей. Это даст возможность оценивать параметры шума и моменты высоких порядков оценки состояния системы. Такой прием используется для обхода ограничения на спектральные характеристики помех. При этом выражения (54) и (57) применяются без своих первых слагаемых, поскольку шумы могут быть не аддитивными, а их статистические характеристики теперь тоже оцениваются. Обновлять состояние системы теперь придется для каждой из точек, сгенерированных на этапе экстраполяции, таким образом воздействие шума на параметры цели пройдет нелинейное преобразование и на шаге обновления состояния. Расширение вектора состояния неизбежно приведет к возрастанию вычислительной сложности алгоритма, однако в ряде практических ситуаций это единственный рациональный способ ухода от допущений об аддитивных БГШ [17], [18]. В остальных случаях стараются пренебречь временной и взаимной корреляцией шумов.
На
рисунке 4 изображен пример нелинейного
преобразования ПРВ двумерной нормальной
случайной величины, аппроксимированной
рассмотренными методами. Случайный
вектор 
подвергается нелинейному преобразованию
,
соответствующему переводу из полярных
в декартовые координаты. Рисунок
х отражает принципиальные различия
между способами аппроксимации различных
нелинейных фильтров.
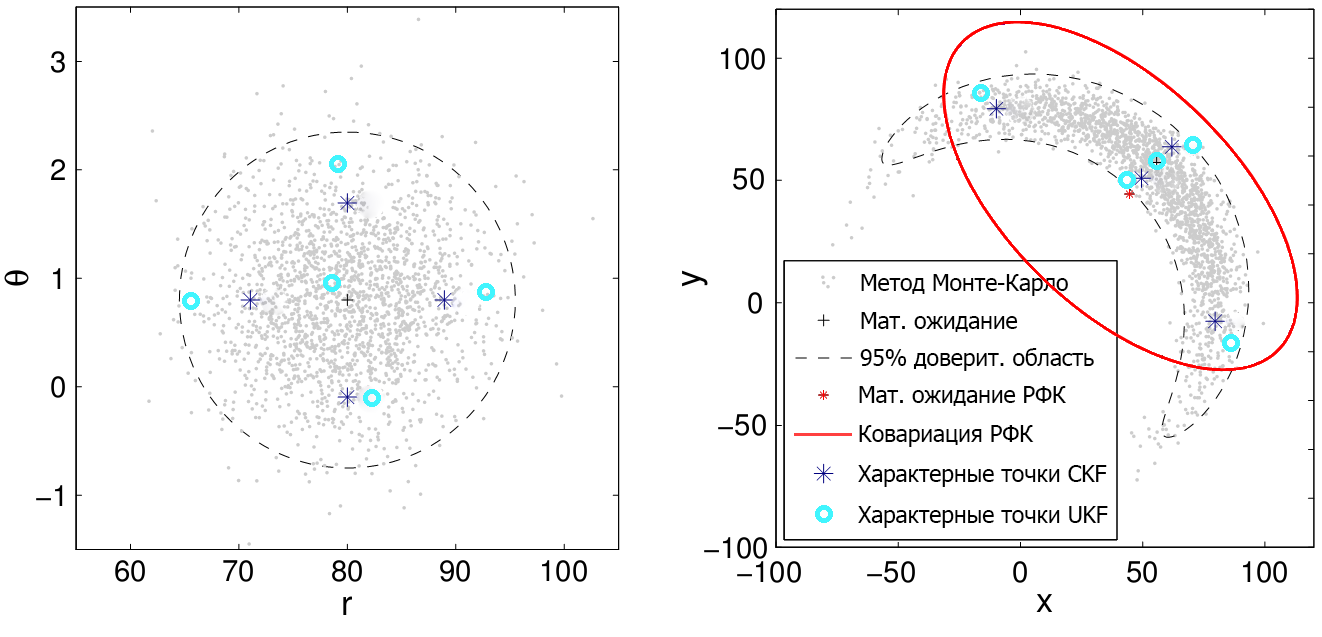Рисунок
4. Аппроксимация распределения двумерной
нормальной случайной величины различными
методами до и после нелинейного
преобразования
Наиболее полно преобразованное распределение двумерной случайной величины аппроксимируется методом генерации случайных величин) монте-карло, используемом в фильтре частиц. РФК ‒ гауссова аппроксимация. По характерным точкам UKF и CKF также получают гауссову аппроксимацию двумерной случайной величины.