Задача 4, вариант 4-1
Условие:
Условие:
Требуется повысить ударную вязкость (у) листового материала из деформируемого алюминиевого сплава при изменении содержания в нем цинка (х1), толщины листа (х2), температуры старения (х3) и времени старения (х4).
В качестве основного уровня и интервалов варьирования выбраны соответственно для:
содержания цинка (%) – 6 и 1;
толщины листа (мм) – 9 и 1;
температуры старения (ºС) – 460 и 10;
времени старения (час) – 14 и 4.
8 опытов плана дали следующие результаты:
№1 – 6,75; № 2 – 5,25; № 3 – 5,75; № 4 – 4,25;
№ 5 – 7,50; № 6 – 8,50; № 7 – 7,00; № 8 – 5,50.
3 опыта на основном уровне дали следующие результаты:
№ 9 – 5,75; № 10 – 6,25; № 11 – 7.00.
В качестве плана эксперимента выбрать дробную реплику 24-1 с величиной определяющего контраста 1=х1х2х3х4
Задание.
1. Составить таблицу условий эксперимента.
2. Составить план эксперимента, состоящий из 8 опытов. В план включить еще 3 опыта на основном уровне. В качестве плана выбрать дробную реплику 24-1 с заданной величиной определяющего контраста 1=х1х2х3х4 . Построить систему оценок коэффициентов регрессии. План записать в кодовом (нормализованном) и натуральном масштабах.
3. По данным опытов на основном уровне определить дисперсию и среднеквадратичную ошибку опыта.
4. Рассчитать коэффициенты регрессии и их доверительные интервалы.
5. Записать линейную модель и формулы перехода от кодированных значений факторов к натуральным значениям.
6. Проверить адекватность линейной модели по t- и F- критериям.
7. Наметить опыты крутого восхождения по градиенту линейной модели.
Решение:
1. Составим таблицу условий проведения эксперимента.
-
Уровень
Факторы
X1 (содержание цинка)
X2 (толщина листа)
X3 (температура старения)
X4 (время старения)
Основной
6
9
460
14
Интервал
варьирования
1
1
10
4
Верхний
7
10
470
18
Нижний
5
8
450
10
2.
Рассмотрим построение плана эксперимента
24-1.
Здесь n = 4, к =1, N=24-1=8.
Факторы X1,
X2,
X3варьируем,
а для фактора X4
выбираем
генерирующее соотношение в виде
(
).
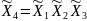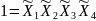Запишем план эксперимента в нормализованном масштабе:
-
Номер
опыта
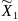
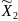
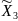
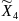
Y
1
-1
-1
-1
-1
6,75
2
+1
-1
-1
+1
5,25
3
-1
+1
-1
+1
5,75
4
+1
+1
-1
-1
4,25
5
-1
-1
+1
+1
7,5
6
+1
-1
+1
-1
8,5
7
-1
+1
+1
-1
7,0
8
+1
+1
+1
+1
5,5
9
0
0
0
0
5,75
0
0
0
0
6,25
0
0
0
0
7,0
Запишем план эксперимента в натуральном масштабе:
-
Номер
опыта
X1
X2
X3
X4
Y
1
5
8
450
10
6,75
2
7
8
450
18
5,25
3
5
10
450
18
5,75
4
7
10
450
10
4,25
5
5
8
470
18
7,5
6
7
8
470
10
8,5
7
5
10
470
10
7,0
8
7
10
470
18
5,5
9
6
9
450
14
5,75
6
9
450
14
6,25
6
9
450
14
7,0
Определяющим контрастом является . Умножая определяющий контраст последовательно на , , и , найдем совместно оценки линейных эффектов и взаимодействий:
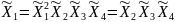
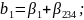
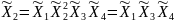
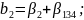
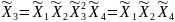
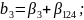
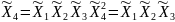
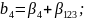
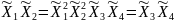
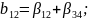
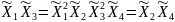
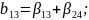
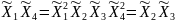
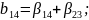
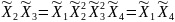
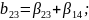
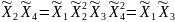
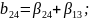
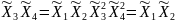
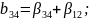
В
практических задачах тройные и более
высокого порядка взаимодействия
значительно чаще, чем двойные, бывают
равны нулю и ими обычно можно пренебречь.
Учтем только парные взаимодействия
,
,
,
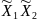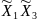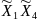так как число
значимых коэффициентов уравнения
регрессии не должно превышать число
опытов (чтобы в дальнейшем проверить
гипотезу об
адекватности полученной математической
модели результатам эксперимента с
использованием критерия Фишера).
Зная результаты опытов, запишем:
-
Номер
опыта
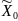
Y
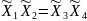
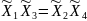
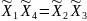
1
1
-1
-1
-1
-1
6,75
1
1
-1
2
1
+1
-1
-1
+1
5,25
-1
-1
-1
3
1
-1
+1
-1
+1
5,75
-1
1
1
4
1
+1
+1
-1
-1
4,25
1
-1
1
5
1
-1
-1
+1
+1
7,5
1
-1
1
6
1
+1
-1
+1
-1
8,5
-1
1
1
7
1
-1
+1
+1
-1
7,0
-1
-1
-1
8
1
+1
+1
+1
+1
5,5
1
1
-1
9
1
0
0
0
0
5,75
0
0
0
1
0
0
0
0
6,25
0
0
0
1
0
0
0
0
7,0
0
0
0
3. Каждая серия содержит только один опыт, для определения дисперсии опыта в центре плана проводится серия из 3 опытов.
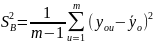
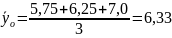
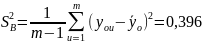
Соответственно дисперсия воспроизводимости:
,
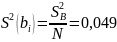где N – число опытов в серии.
Среднеквадратичная
ошибка:
.
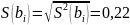4. Определение параметров нормализованной линейной модели производится по формулам:
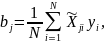
где
j
= 1,…, k.
k
– число факторов; i
= 1,…, N.
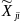– значение фактора
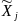в i-ом
опыте.
;
;
;
;
;
;
;
;
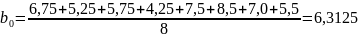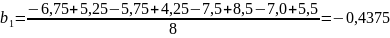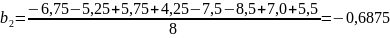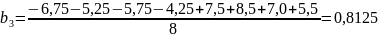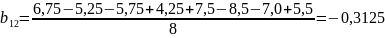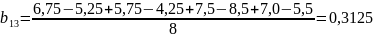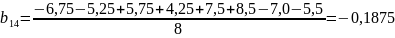Доверительный
интервал
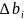- находят по
формуле
,
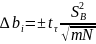где
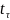определим из
Приложения 6 [1] при
5% - ном уровне значимости и числе
степеней свободы f=mN.
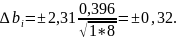
5. Линейная модель имеет вид:
.
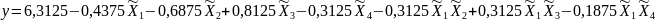Уравнения регрессии для натуральных, а не кодированных значений факторов, можно получить, используя формулу перехода
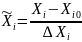
При этом коэффициенты регрессии изменяются и возможность интерпретации влияния факторов по величинам и знакам коэффициентов регрессии пропадет, зато появляется возможность прогнозировать результаты опытов (значения выходного параметра) при любых натуральных значениях факторов в исследованной области факторного пространства, что имеет большое практическое значение.
;
;
;
.
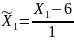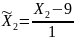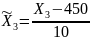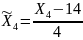6. Проверим адекватность линейной модели по t- критерию Стъюдента. Для этого:
а) вычисляем оценку дисперсии параметра оптимизации
.
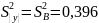б) вычисляем оценку дисперсии коэффициента полинома
.
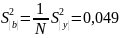в) для каждого из вычисленных коэффициентов считаем величину:
,
где g=0, 1, …n.
;
;
;
.
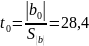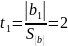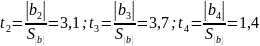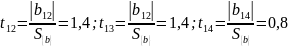г) По числу степеней свободы f=mN и при выбранном уровне значимости 5% определяем величину из Приложения 6 [1].
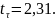
Коэффициенты
,
,
,
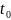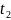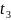больше
,
следовательно, данные коэффициенты
значимы.
Проверим гипотезу об адекватности полученной математической модели результатам эксперимента с использованием критерия Фишера.
В нашем случае число значимых коэффициентов уравнения регрессии равно числу опытов, т.е. степень свободы дисперсии адекватности равна нулю. Поэтому мы вынуждены поставить дополнительный опыты на нулевом уровне. Результаты опыта заносим в план эксперимента. При этом число опытов N становится равным 9, а дисперсия воспроизводимости
.
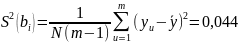По
уравнению регрессии рассчитываем
значения
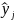и определяем сумму квадратов отклонений
.
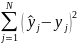Результаты расчета заносим в таблицу
плана эксперимента.
Номер |
|
|
|
|
Y |
|
|
1 |
-1 |
-1 |
-1 |
-1 |
6,75 |
6,75 |
0 |
2 |
1 |
-1 |
-1 |
1 |
5,25 |
5,25 |
0 |
3 |
-1 |
1 |
-1 |
1 |
5,75 |
5,75 |
0 |
4 |
1 |
1 |
-1 |
-1 |
4,25 |
4,25 |
0 |
5 |
-1 |
-1 |
1 |
1 |
7,5 |
7,5 |
0 |
6 |
1 |
-1 |
1 |
-1 |
8,5 |
8,5 |
0 |
7 |
-1 |
1 |
1 |
-1 |
7 |
7 |
0 |
8 |
1 |
1 |
1 |
1 |
5,5 |
5,5 |
0 |
9 |
0 |
0 |
0 |
0 |
5,75 |
6,3125 |
0,3164 |
0 |
0 |
0 |
0 |
6,25 |
6,3125 |
0,0039 |
|
0 |
0 |
0 |
0 |
7 |
6,3125 |
0,4727 |
|
Σ |
|
|
|
|
|
|
0,7930 |
Находим дисперсию адекватности для N = 9 и d =8:
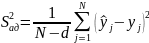=0,793.
Модель адекватна, если выполняется неравенство
,
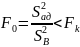где
,
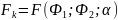Ф1
= N(m -1); Ф2
= N - d.
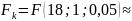249.
.
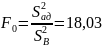Получаем F0 < Fk и, следовательно, уравнение регрессии адекватно экспериментальным результатам.
7. Наметить опыты крутого восхождения по градиенту линейной модели.
Переходим к натуральным значениям факторов по формулам
; ; ; .
.
.
.
.
.
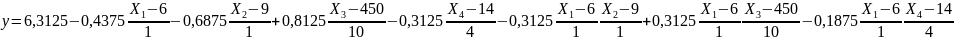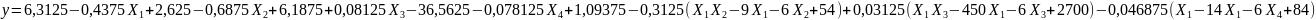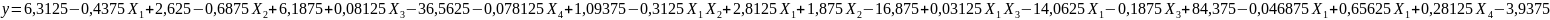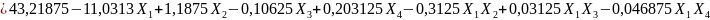Если описание поверхности отклика в общем случае у = f(х1, х2, x3, х4), то градиент функции
.
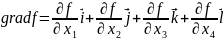Градиент
целесообразно определять в точке А, где
при проведении эксперимента было
получено наилучшее значение параметра
оптимизации. Точка А имеет координаты
,
,
,
.
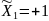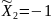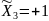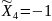Как показали
Бокс и Уилсон, коэффициенты bi
уравнения имеют смысл частных производных
функции отклика.
.
;
;
;
;
;
;
;
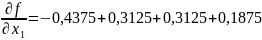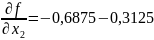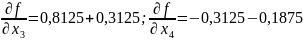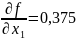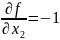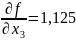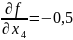Фактор,
для которого абсолютное значение
составляющей градиента оказалось
максимальным(X3),
принимается за базовый. Для этого фактора
принимается шаг движения по градиенту
.
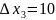Шаги для остальных экспериментов
определяются по формуле:
.
;
;
.
-
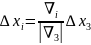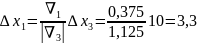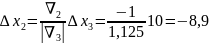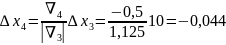Условия эксперимента
Факторы
Значения отклика
X1
X2
X3
X4
Yэксп
Yрасч
Основной уровень
6
9
460
14
7,1247
Интервал
варьирования
1
1
10
4
Шаг
3,3
-8,9
10
-0,044
Условия опытов
1
9,3
0,1
470
13,956
23,8629
2
12,6
-8,8
480
13,912
61,03347
3
15,9
-17,7
490
13,868
118,6364
4
19,2
-26,6
500
13,824
196,6717
Об эффективности движения по градиенту можно судить по значению параметра оптимизации. Движение эффективно, если реализация опытов эксперимента приводит к улучшению параметра оптимизации по сравнению с наилучшим результатом в матрице откликов, по которой строилась модель.
После продвижения на один или несколько шагов по направлению к оптимуму, проводят опыты по плану ПФЭ или ДФЭ. По результатам опыта строят модель, которая описывает новое факторное пространство.
Снова определяют градиентное направление и шаг движения в этом направлении. Затем осуществляют движение на один или несколько шагов в новом направлении, и алгоритм действий экспериментатора повторяется. Так, шаг за шагом достигаются все более высокие значения отклика.
Гмурман В.Е. Теория вероятностей и математическая статистика, М., 2003, 480 с.