Контрольная работа Специальные разделы математики Вариант 25

48. Интерполяционная и экстремальная задачи планирования эксперимента. Понятие последовательного планирования эксперимента. Что такое «матрица условий эксперимента» и «матрица наблюдений»?

Чаще всего активный эксперимент ставят для решения одной из двух основных задач. Первую задачу называют экстремальной. Она заключается в отыскании условий процесса, обеспечивающих получение оптимального значения выбранного параметра. Признаком экстремальных задач является требование поиска экстремума некоторой функции (*проиллюстрировать графиком*). Эксперименты, которые ставят для решения задач оптимизации, называют экстремальными.

Вторую задачу называют интерполяционной. Она состоит в построении интерполяционной формулы для предсказания значений изучаемого параметра, зависящего от ряда факторов.

Для решения экстремальной или интерполяционной задачи необходимо иметь математическую модель исследуемого объекта. Модель объекта получают, используя результаты опытов.

В теории планирования эксперимента сознательно отказываются от полного перебора входных состояний или от эксперимента, близкого к нему по своей конструкции. Выбор числа уровней варьирования по каждому фактору связан с видом функции отклика или, точнее, с выбором вида ее аппроксимации (в частности, в наиболее распространенных полиномиальных регрессионных моделях – со степенью аппроксимирующего полинома).

В свою очередь, этот выбор можно осуществить, используя принцип постепенного усложнения математической модели (принцип последовательного планирования). В отсутствие априорной информации о свойствах функции отклика нет смысла сразу строить сложную модель объекта, получение которой требует большего числа опытов, чем модели простой. В результате может оказаться, что в сложной модели нет необходимости, что она вырождается в простую, поскольку таковы свойства объекта. С точки зрения конечного результата – это хорошо, но напрасно затраченные на проведение лишних опытов время и средства уже не вернешь. Поэтому теория планирования эксперимента рекомендует начинать с простейшей модели, соответствующей имеющейся априорной информации (например, с линейной модели, если нет никакой информации о свойствах объекта, или он не обладает ярко выраженными нелинейными свойствами; или с квадратичной модели, если известно, что функция отклика, по всей видимости, не линейна).

Логика эксперимента такова: постановка небольшого числа опытов для получения простейшей модели, проверка ее пригодности; если модель удовлетворяет исследователя, эксперимент заканчивается. Если же модель непригодна, необходим следующий этап экспериментирования: постановка новых опытов, позволяющих получить более сложную модель, ее проверка и т.д. до тех пор, пока не будет получена модель, которую исследователь признает достаточно хорошей.

При проведении многофакторного эксперимента, все множество уровней факторов, при которых проводится измерение отклика, задается матрицей условий эксперимента:

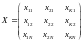, где К – число контролируемых факторов, N – число опытов (измерений). Значения отклика, полученные для каждого из 1…N измерений, представляют в виде матрицы наблюдений.

.
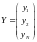