
- •23). Матрицы. Операции над ними. Свойства матриц.
- •24). Определители 2 и 3 порядков. Их вычисление. Свойства определителей. Теорема о разложении определителем по элементам строки (столбца).
- •25). Миноры и алгебраические дополнения. Обратная матрица(условие её существования и вычисление).
- •26). Решение систем n линейных уравнений с n неизвестными по правилу Крамера и методом обратной матрицы.
- •27). Правило суммы и произведения в комбинаторике. Сочетания из n элементов по m. Формулы для их вычисления.
- •29). Формула полной вероятности. Формула Байеса.
- •30). Независимые повторные испытания. Формула Бернулли.
- •31). Дискретные случайные величины. Закон распределения случайной величины. Функция распределения случайной величины. Её свойства.
- •32. Числовые характеристики случайной величины: математическое ожидание, дисперсия, среднеквадратическое отклонение.
- •18). Смешанное произведение векторов. Свойства, вычисление, применение.
- •17). Векторное произведение векторов. Свойства, вычисление, применение.
- •16). Скалярное произведение векторов. Свойства, вычисление, применение.
- •15). Геометрические векторы. Действия над векторами. Свойства операций над векторами.
- •14). Дифференциальные уравнения 2-го порядка со специальной правой частью. Их общее решение.
- •13). Однородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вид общего решения в зависимости от корней характеристического уравнения.
- •12). Неоднородные и однородные дифференциальные уравнения 2 порядка. Теорема об общем решении однородного уравнения. Теорема об общем решении неоднородного уравнения.
- •11). Дифференциальные уравнения 2-го порядка. Решение дифференциального уравнения 2-го порядка. Общее решение. Частное решение. Задача Коши. Теорема Коши.
13). Однородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вид общего решения в зависимости от корней характеристического уравнения.
y’’-py’+qy=0, где p,q R.
Общее решение:
y’=k*ekx ; y’’=k2* ekx.
k2* ekx+p*k*ekx+q* ekx=0.
ekx(k2+ p*k+q)=0.
k2+ p*k+q=0- характеристическое уравнение.
K1,2=-(p/2)±√(p2/4-q).
Хар.уравнен. |
Дискриминант |
Корни |
Общее решение |
x2+ px+q=0 |
(p2/4-q)>0 |
K1,k2 R ,k1 не равно k2. |
y=c1* ek1x+ c2* ek2x |
(p2/4-q)=0 |
K1,k2 R, K1=k2=k. |
y=c1* ekx+ c2* x*ekx |
|
(p2/4-q)<0 |
K1,k2
не
|
y=eαx(c1*cosβ*x+c2*sinβ*x) |
12). Неоднородные и однородные дифференциальные уравнения 2 порядка. Теорема об общем решении однородного уравнения. Теорема об общем решении неоднородного уравнения.
Однородное линейное дифференциальное уравнение 2-го порядка имеет вид:
![]() где p,
q − постоянные коэффициенты.
где p,
q − постоянные коэффициенты.
Линейное
неоднородное уравнение 2 порядка имеет
вид:![]()
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными).
Теорема об общего решения линейного однородного дифференциального уравнения: Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x).
Теорема
об общем решении неоднородного уравнения:
Общее решение неоднородного уравнения
является суммой общего
решения y0(x) соответствующего
однородного уравнения и частного
решения y1(x) неоднородного
уравнения:![]() .
.
11). Дифференциальные уравнения 2-го порядка. Решение дифференциального уравнения 2-го порядка. Общее решение. Частное решение. Задача Коши. Теорема Коши.
Дифференциальным уравнением второго порядка называется уравнение вида:
![]() где
х — независимая переменная, у — искомая
функция, у' и у" — соответственно ее
первая и вторая производные.
где
х — независимая переменная, у — искомая
функция, у' и у" — соответственно ее
первая и вторая производные.
Определение. Общим
решением уравнения второго порядка
называется такая функция ![]() ,
которая при любых значениях
,
которая при любых значениях ![]() и
и ![]() является
решением этого уравнения.
является
решением этого уравнения.
Уравнение ![]() ,
определяющее общее решение, называется
общим интегралом дифференциального
уравнения.
,
определяющее общее решение, называется
общим интегралом дифференциального
уравнения.
Если в общее решение
подставить конкретные значения ![]() и
и ![]() ,
то получится частное
решение дифференциального уравнения.
,
то получится частное
решение дифференциального уравнения.
Зада́ча Коши́ —состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего начальным данным. Например, для уравнения dy = 2xdx можно поставить Коши задачу: найти решение у = у(х), принимающее при хо = 0 значение уо = 1; оно таково: у = х2 + 1.
Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка, причем h’y(x) № 0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство
|
|||||
10). Линейное дифференциальное уравнение первого порядка. Методы его решения. Линейным дифференциальным уравнением первого порядка называется уравнение вида
Метод Бернулли. Пусть
дано уравнение (1). Решение этого
уравнения будем искать в виде
произведения двух функций:
Найдем такую функцию
Тогда решение уравнения (1) будет сведено к решению системы уравнений с разделяющимися переменными
Заметим, что при решении первого уравнения системы достаточно указать любое частное решение, то есть выбор константы произволен.
Решим уравнение
(2):
Получено уравнение с
разделяющимися переменными относительно
неизвестной функции
Из уравнения (4) имеем
9). Уравнения с разделяющимися переменными. Методы его решения. Уравнение с разделяющимися переменными – уравнение вида P(x)dx+Q(y)dy=0.
Метод решения
– интегрирование обеих частей:
P1(x)*Q1(y)dx+P2(x)*Q2(y)dy=0
|:(Q1(y)*P2(x))
8). Дифференциальные уравнения первого порядка. Решение дифференциального уравнения. Общее решение. Частное решение. Задача Коши. Теорема Коши. Дифференциальное уравнение первого порядка - уравнение, связывающее независимую переменную x, искомую функцию y=y(x) и ее первую производную y’, т.е. уравнение вида F(x,y,y’)=0 или y’=f(x,y). Решением дифференциального уравнения называется функция y=j(x), такая, что при подстановке в уравнение обращает его в тождество. Задачей Коши
называют задачу нахождение
решения y=y(x) уравнения y’=f(x), удовлетворяющего
начальному условию
Теорема Коши: пусть
дано дифференциальное уравнение y¢=f(x;y),
где f(x,y) определена
в некоторой области Д плоскости XOY,
содержащей точку
а) f(x,y) есть
непрерывная функция двух переменных x и y в
области Д;
б) если f(x,y) имеет
частную производную Функция y=j(x,c), зависящая от аргумента x и произвольной постоянной c, называется общим решением уравнения (1) в области Д, если она удовлетворяет условиям: 1) при любых значениях произвольной постоянной c, принадлежащих некоторому множеству, y=j(x,c) является решением уравнения (1); 2) какова бы ни была точка (x0;y0), лежащая внутри области Д, существует единственное значение постоянной c=c0 , такое, что решение y=j(x,c) удовлетворяет начальному условию y(x0)=y0 .
Всякое решение 7). Условный экстремум функции нескольких переменных. Методы нахождения условного экстремума (метод частичного исключения и метод неопределённых множителей Лагранжа).
Условный экстремум
ФНП: Точка (x0;y0)
называется точкой условного
max(min), если
существует такая окрестность этой
точки, что для всех (x.y)
из этой окрестности удовлетворяющих
условию g(x,y)
=C, выполняется неравенство
f(x0,y0) Нахождение наибольшего и наименьшего значения функции - Функция дифференцированная и ограниченная в замкнутой области достигает своего наибольшего( наименьшего) значения либо во внутренних точках, либо на границе замкнутой области. Алгоритм: 1. Найти стационарные точки внутренней области z’x=0 z’y=0 2.Вычислить в стационарных точках значение функции. 3. Найти наименьшее и наибольшее значение ограничивающей области . 4.Выбрать из всех полученных значений наибольшее и наименьшее значение. Функция Лагранжа:
L(x,y, 6). Экстремумы функции нескольких переменных. Необходимое и достаточное условия существования экстремума функции двух переменных. Экстремум функции
нескольких переменных: Точка М(x0,y0)
называется точкой max(min)
функции z =f(x,y),
если существует такая окрестность
точки М, что для всех точек (x,y)
из этой окрестности выполняется
неравенство f(x0,y0) Необходимое условие: Пусть точка (x0,y0) – есть точка экстремума дифференцируемой функции z = f(x,y). Тогда частные производные f’x(x0,y0) и f’y(x0,y0) в этой точке равны нулю. Точки, в которых выполнены необходимые условия экстремума функции называются критические или стационарными. Достаточное
условие: Пусть функция z=f(x,y)
а) определена в некоторой окрестности
критической точки М0, в которой
f’x(M0)=0
и f’y(M0)=0;
б) имеет в этой точке непрерывные
частные производные второго порядка
f’xx(M0)=A,
f’xy(M0)
= B, f’yy(M0)
= C. Тогда если АС- A<0 – max. Если AC- <0, то в стационарной точке нет экстремума. Если АС- =0, то требуется дополнительное исследование. 5). Дифференцирование сложных и неявно заданных функций. Правило дифференцирования сложной функции: Если функция f имеет производную в точке х0, а функция g имеет производную в точке y0=f(x0) , то сложная функция h(x) = g(f(x)) также имеет производную в точке Пример: Пусть
даны функции, определённые в окрестностях
на числовой прямой,
В обозначениях
Лейбница правило для вычисления
производной функции
4). Дифференциал функции нескольких переменных. Пусть функция z = f(x,y), имеет в точке М0(х0,у0) частные производные f /x (х0,у0) и f /у (х0,у0). Полным приращением функции z = f(x,y) в точке М0(х0,у0) называется разность
Пусть приращение функции
z =f(x,y) можно представить в виде
Полным дифференциалом
функции z=f(x,y) называется главная
часть полного приращения
Дифференциалы dх и dy
независимых аргументов функции х и у
совпадают с их приращениями соответственно
. Таким образом, 3). Частные производные функции нескольких переменных. Их геометрический смысл. Частной производной
функции нескольких переменных по
одной из этих переменных называется
предел отношения соответствующего
частного приращения функции к приращению
рассматриваемой независимой переменной
при стремлении последнего к нулю.
Геометрический смысл частных производных:
Согласно геометрическому смыслу
производной функции одной
переменной f(x, y0)
, α является углом между
осью OX и касательной к графику
этой функции, т.е. к кривой, определяемой
системой уравнений: 2). Пределы и непрерывность функции нескольких переменных.
Число A называется
пределом функции
Обозначают: Функция нескольких переменных называется бесконечно малой, если ее предел равен нулю.
Функция
1) функция
2) существует предел
3) этот предел равен значению
функции в предельной точке: 1). Выделение функции нескольких(2) переменных. Область определения. Множество значений. Изображение функции двух переменных.
Определение. Переменная
1) задано
множество
2) задан
закон, по которому каждой паре чисел Множество всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.
Например, областью
определения функции Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность.
|


 ,
,  ,
,  -общий
интеграл.
-общий
интеграл.

 .
При деление обеих частей уравнения
на Q1(y)+P2(x)=0
могут потерятся решения этого уравнения,
значит нужно рассмотреть и решить его
отдельно и получить корни, которые не
входят в общее решение dy.
Такие решения- особые
решения.
Пример:
.
При деление обеих частей уравнения
на Q1(y)+P2(x)=0
могут потерятся решения этого уравнения,
значит нужно рассмотреть и решить его
отдельно и получить корни, которые не
входят в общее решение dy.
Такие решения- особые
решения.
Пример:
 ;
; ;
y=f(x),dy=y’dx.
y=x2с
– общее решение этого диффиренциального
уравнения, при с
;
y=f(x),dy=y’dx.
y=x2с
– общее решение этого диффиренциального
уравнения, при с R.
R.
 ,
ограниченную в области Д, то
найдется интервал(x0-h,x0+h),
на котором существует единственное
решение y=j(y) данного
уравнения, удовлетворяющее условию
y(x0)=y0 .
,
ограниченную в области Д, то
найдется интервал(x0-h,x0+h),
на котором существует единственное
решение y=j(y) данного
уравнения, удовлетворяющее условию
y(x0)=y0 . f(x,y)
(f(x0,y0)
f(x,y)
(f(x0,y0) f(x,y)).
f(x,y)). )=f(x,y)+λ[g(x,y)-C].
Если точка (x0,y0)
является точкой условного экстремума
функции z=f(x,y)
при условии g(x,y)=C,
то существует значение λ0 такое,
что точка (x0,y0,λ0)
является точкой экстремума функции
L(x,y,λ).
)=f(x,y)+λ[g(x,y)-C].
Если точка (x0,y0)
является точкой условного экстремума
функции z=f(x,y)
при условии g(x,y)=C,
то существует значение λ0 такое,
что точка (x0,y0,λ0)
является точкой экстремума функции
L(x,y,λ). f(x,y)
(f(x0,y0)
f(x,y)
(f(x0,y0) f(x0,y0)).
f(x0,y0)). >0 – то экстремум существует, причём
А>0 – min
>0 – то экстремум существует, причём
А>0 – min
 ;
;
 .
.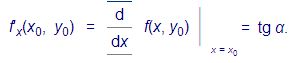 .
.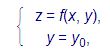 в
точке (x0, y0, z0)
, где z0 = f(x0,
y0) (рис. 1):
в
точке (x0, y0, z0)
, где z0 = f(x0,
y0) (рис. 1):