
- •23). Матрицы. Операции над ними. Свойства матриц.
- •24). Определители 2 и 3 порядков. Их вычисление. Свойства определителей. Теорема о разложении определителем по элементам строки (столбца).
- •25). Миноры и алгебраические дополнения. Обратная матрица(условие её существования и вычисление).
- •26). Решение систем n линейных уравнений с n неизвестными по правилу Крамера и методом обратной матрицы.
- •27). Правило суммы и произведения в комбинаторике. Сочетания из n элементов по m. Формулы для их вычисления.
- •29). Формула полной вероятности. Формула Байеса.
- •30). Независимые повторные испытания. Формула Бернулли.
- •31). Дискретные случайные величины. Закон распределения случайной величины. Функция распределения случайной величины. Её свойства.
- •32. Числовые характеристики случайной величины: математическое ожидание, дисперсия, среднеквадратическое отклонение.
- •18). Смешанное произведение векторов. Свойства, вычисление, применение.
- •17). Векторное произведение векторов. Свойства, вычисление, применение.
- •16). Скалярное произведение векторов. Свойства, вычисление, применение.
- •15). Геометрические векторы. Действия над векторами. Свойства операций над векторами.
- •14). Дифференциальные уравнения 2-го порядка со специальной правой частью. Их общее решение.
- •13). Однородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вид общего решения в зависимости от корней характеристического уравнения.
- •12). Неоднородные и однородные дифференциальные уравнения 2 порядка. Теорема об общем решении однородного уравнения. Теорема об общем решении неоднородного уравнения.
- •11). Дифференциальные уравнения 2-го порядка. Решение дифференциального уравнения 2-го порядка. Общее решение. Частное решение. Задача Коши. Теорема Коши.
29). Формула полной вероятности. Формула Байеса.
Формула Байеса: P(H1\A)
=

Формула полной
вероятности: Если событие А может
произойти только при выполнении одного
из событий ![]() ,
которые образуют полную группу
несовместных событий, то вероятность
события Авычисляется по формуле
,
которые образуют полную группу
несовместных событий, то вероятность
события Авычисляется по формуле
![]() .
.
30). Независимые повторные испытания. Формула Бернулли.
Испытания независимые, если вероятность каждого исхода не зависит от того, какие исходы имели другие опыты, т.е. вероятность каждого исхода остается постоянной от опыта к опыту.
Пусть производится ![]() независимых
опытов, в каждом из которых может
появиться или не появиться событие
независимых
опытов, в каждом из которых может
появиться или не появиться событие ![]() .
Причем вероятность появления события
в каждом опыте равна
.
Причем вероятность появления события
в каждом опыте равна ![]() ,
а вероятность непоявления равна
,
а вероятность непоявления равна ![]() .
Требуется найти вероятность
.
Требуется найти вероятность ![]() того,
что в
независимых
опытах событие
произойдет ровно
того,
что в
независимых
опытах событие
произойдет ровно ![]() раз. Найдем вероятность
.
Возьмем
букв
и
раз. Найдем вероятность
.
Возьмем
букв
и ![]() букв
букв ![]() и
будем их между собой переставлять.
Каждая перестановка соответствует
определенной очередности появления
или непоявления события
.
Например,
и
будем их между собой переставлять.
Каждая перестановка соответствует
определенной очередности появления
или непоявления события
.
Например, ![]() соответствует
ситуации, в которой событие появилось
в первом опыте, во втором и третьем не
появилось, появилось в четвертом и т.д.
Всего вариантов будет столько, сколькими
способами можно из
мест
выбрать
различных
(порядок не важен!) и поставить на них
букву
,
т.е.
соответствует
ситуации, в которой событие появилось
в первом опыте, во втором и третьем не
появилось, появилось в четвертом и т.д.
Всего вариантов будет столько, сколькими
способами можно из
мест
выбрать
различных
(порядок не важен!) и поставить на них
букву
,
т.е. ![]() способов.
Вероятность любого из этих способов (в
силу независимости опытов, а значит, и
событий) равна по теореме умножения
вероятностей
способов.
Вероятность любого из этих способов (в
силу независимости опытов, а значит, и
событий) равна по теореме умножения
вероятностей ![]() .
Появление хотя бы одного из
этих
несовместных
исходов приводит к появлению интересующего
нас события, поэтому
.
Появление хотя бы одного из
этих
несовместных
исходов приводит к появлению интересующего
нас события, поэтому
![]()
Или
![]() -
Это и есть формула
Бернулли.
-
Это и есть формула
Бернулли.
31). Дискретные случайные величины. Закон распределения случайной величины. Функция распределения случайной величины. Её свойства.
Дискретная случайная величина - такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.
Закон распределения случайной величины - всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Функция распределения вероятностей F(x) случайной величины Х в точке х - вероятность того, что в результате опыта случайная величина примет значение, меньше, чем х, т.е. F(x)=P{X < х}.
Свойства функции F(x): 1. F(-∞)=lim(x→-∞)F(x)=0. 2. F(∞)=lim(x→∞)F(x)=1, так как по определению, F(∞)=P{X < ∞}. Событие Х < ∞ является достоверным событием. Следовательно, F(∞)=P{X < ∞}=p{U}=1. 3. P{Α ≤X<Β}=F(Β)-F(Α).
4. F(x2)≥ F(x1 ), если x2, > x1. 5. Функция распределения вероятностей непрерывна слева.
32. Числовые характеристики случайной величины: математическое ожидание, дисперсия, среднеквадратическое отклонение.
Математическое ожидание - среднее
значение случайной
величины,
распределение вероятностей случайной
величины:
M(X)
=

Дисперсия - мера
разброса данной случайной
величины,
то есть её отклонения от математического
ожидания.:
D(x)
= M(
Среднеквадрати́ческое
отклоне́ние -
наиболее
распространённый показатель рассеивания
значений случайной
величины относительно
её математического
ожидания:
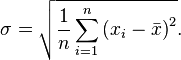
22). Системы линейных уравнений. Решение системы. Совместные, несовместные, определённые, неопределённые системы линейных уравнений. Равносильные системы. Элементарные преобразования системы. Теорема об элементарных преобразованиях. Метод Гаусса.
Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных:

Решение системы уравнений — это последовательность чисел (k1, k2, ..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1,x2, ..., xn дает верное числовое равенство. решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто.
Система несовместна, т.е. множество всех решений пусто.
Система совместна и определена, т.е. имеет ровно одно решение.
Система совместна и не определена, т.е. имеет бесконечно много решений.
Две линейные системы уравнений называются равносильными, если множества решений этих уравнений совпадают.
Элементарными преобразованиями системы линейных уравнений называются:
1. умножение уравнения на отличное от нуля число;
2. прибавление к одному уравнению любого другого, умноженного на любое число;
3. перестановка уравнений местами.
Теорема. Любая система линейных уравнений с помощью элементарных преобразований и, может быть, изменением нумерации неизвестных, может быть приведена к системе с трапециевидной матрицей.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:
На первом этапе среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе выражают все получившиеся базисные переменные через небазисные и строят фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
21). Прямая в пространстве. Виды уравнений прямой в пространстве.
Виды уравнений прямой в пространстве:
1). Пересечение 2 плоскостей. Общее уравнение прямой:
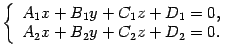
2). Каноническое уравение прямой:
![]() - канонические
уравнения прямой в пространстве,
проходящей через точку
- канонические
уравнения прямой в пространстве,
проходящей через точку ![]() параллельно
вектору
параллельно
вектору ![]()
3). Параметрическое уравение прямой:
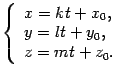
4). Уравнение прямой, проходящей через 2 заданные точки:
![]()
![]()
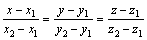
20). Плоскость в пространстве. Виды уравнений плоскости в пространстве.
Виды уравнений плоскости в пространстве:
 –
уравнение
плоскости, проходящей через
точку
–
уравнение
плоскости, проходящей через
точку 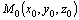 перпендикулярно
нормальному вектору
перпендикулярно
нормальному вектору 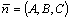 .
. –
общее уравнение
плоскости, где
-
нормальный вектор плоскости, т.е.
перпендикулярный к плоскости.
–
общее уравнение
плоскости, где
-
нормальный вектор плоскости, т.е.
перпендикулярный к плоскости. –
уравнение плоскости,
проходящей через три заданные
точки
–
уравнение плоскости,
проходящей через три заданные
точки  ,
, 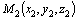 и
и  .
.
19). Прямая на плоскости. Виды уравнений прямой на плоскости.
Уравнение прямой на плоскости в прямоугольной системе координат Oxy - некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой
Виды уравнений прямой на плоскости:
1). y=kx+b,
где k-
угловой коэфициент,
![]() .
.
2). Общее уравнение прямой:
![]() ,
,
![]() -
нормальный вектор прямой.
-
нормальный вектор прямой.
3).уравнение прямой, проходящей через заданную точку в данном направлении: A(x1;y1); y-y1=k(x-x1).
4). Уравнение
прямой, проходящей через 2 заданные
точки: ![]() и
и ![]() ,
,
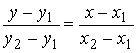 .
.
