23). Матрицы. Операции над ними. Свойства матриц.

Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. М. обозначаются заглавными буквами, для обозначения элементов используют строчные буквы с двойной индексацией: aij, где i – номер строки, j- номер столбца . пример:

A(mxn)=

Действия над матрицами. 1. Умножение на число. Произведением матрицы А на число Х называется матрица В=xА, элементы которой bij= xaij для i=1,2…m, j =1,2…n

2. Сложение матриц. Суммой двух матриц А и В одинакового размера mxn называется матрица С = А+В, элементы которой cij=aij+bij для i =1,2…m j= 1,2..n

3. Вычитание матриц. А-В=А+(-1)*В

4. Транспонирование матрицы - переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка.

5) Умножение матрицы А на матрицу В определённо, когда число столбцов первой матрицы равно числу строк во второй. Аmxk *Bkxn = C mxn , каждый элемент которой сij равен сумме произведений элементов i-й строки и матрицы А на соответствующие элементы j-ого столбца матрицы В.

Свойства операций над матрицами

1) А+В=В+А 2) (А+В)+С=А+(В+С)

3) λ(А+В)=λА+λВ 4) А(B+С)=АВ+АС

5)(А+В)С=АС+ВС 6) λ(АВ) =(λА)В=А(λВ)

7) А(ВС)=(АВ)С 8). A^m=(A*A*…*A) (m paз), при м>1 .

9). A^m*A^k=A^m+k 10). A⁰=E. 11). A¹=A. 12). (A^m)^k=A^mk.

24). Определители 2 и 3 порядков. Их вычисление. Свойства определителей. Теорема о разложении определителем по элементам строки (столбца).

Определитель – число, характеризующие квадратную матрицу А.

Определителем матрицы второго порядка А=(aij) называется число, которое вычисляется по формуле

Определителем матрицы третьего порядка А= aij, называется число, которое вычисляется по формуле: .

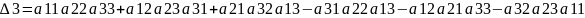Свойства определителей: 1. Если какая-либо строка(столбец) матрицы состоит из нулей, то её определитель=0.

2. если все элементы какой-либо строки(столбца) матрицы умножить на число Х, то её определитель умножится на это же число Х.

3. При транспортировании матрицы её оределитель не изменяется.

4. При перестановке 2 строк(столбцов) матрицы её определитель меняет знак на противоположный.

5. Если квадратная матрица содержит 2 одинаковые Строки(столбца), то её определитель =0.

6. Если элементы 2 строк(столбцов) матрица пропорциональны, то её определитель=0.

7. ⁿЕ_s=1a_isA_js=0, при I не равном j.

8. Определитель матрицы не изменяется, если к элементам какой-либо строки(столбца) матрицы прибавить элементы другой строки(столбца) предварительно умноженные на 1 и то же число.

9. Сумма произведений произвольных чисел b1,b2,b3,…,bn на алеграические дополнения элементов любой строки(столбца)= определителю матрицы, полученной из данной заменой элементов этой строки(столбца) на число b1,b2,b3,…,bn.

10. определитель произведения 2 квадратных матриц= произведению из определителей |C|=|A|+|B|

Теорема о разложении определителя по элементам строки. Определитель матрицы  A  равен сумме произведений элементов строки на их алгебраические дополнения: .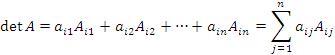

Теорема о разложении определителя по элементам столбца. Определитель матрицы  A  равен сумме произведений элементов столбца на их алгебраические дополнения:

.
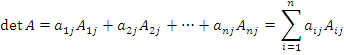