2) Графическое представление (рис.7).

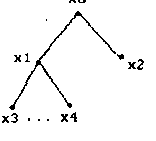
Рис. 7.Графическое представление дерева

Таблицы с вычисляемыми входами

Таблица - это множество записей, организованное таким образом, что каждая запись, а возможно, и ее расположение однозначно определяются заданием так называемого ключа этой записи. Обычно записи состоят из двух по­лей: ключа, ее однозначно определяющего, и тела записи, содержащего собст­венно запись.

Доступ к телу записи можно получить, задавая ее ключ. Поэтому следует основное внимание уделить обработке ключей, только в случае необходимости обращаясь к данным, находящимся в теле записи.

К наиболее распространенным операциям над таблицами относятся:

• включение новой записи в таблицу;

• поиск в таблице записи с указанным ключом;

• исключение из таблицы записи с указанным ключом;

• модификация записи с указанным ключом.

Эффективность и даже возможность применения той или иной операции существенно зависят от того, каким образом сформирована таблица, как она расширяется и как организован доступ к отдельным записям.

Функция f(k) такая, в которой каждому возможному значению ключа кi, где i=l, 2, 3, .,., n, ставит в соответствие одно из чисел в диапазоне от 1 до n. Эта функция называется функцией расстановки или хеш-функцией, а сам процесс вычисления адреса - хешированием.

Таблица, функция расстановки для которой задает взаимно однозначное соответствие между ключами и адресами, называется таблицей с вычисляемым входом (с прямым доступом). В таких таблицах ключ используется непосредст­венно в качестве адреса записи либо адрес вычисляется как значение некото­рой функции от ключа.

Подбор функции расстановки, обеспечивающей взаимную однозначность преобразования ключа в ее адрес в таблице, возможен только для таблиц посто­янного объема с известным конечным множеством значений ключа.

Пример

Предположим, что каждая запись таблицы идентифицируется числовым ключом ki, со значениями от 100 до 999. Число допустимых записей в такой таблице достигает 900. В качестве функции расстановки, однозначно опреде­ляющей для каждого ключа ki, адрес соответствующей записи в таблице f(ki) (адресом записи будем считать ее порядковый номер в таблице), можно пред­ложить функцию f(ki)=ki-100+ l=ki-99, вычисление которой не представляет никаких трудностей.

Один из алгоритмов размещения записи в таблицу:

1. Начало, Вычислить значение функции расстановки f(k)=i.

2. Если i-я позиция таблицы свободна, запись разместить в ней.

1. В противном случае вычислить новое значение номера позиции i=i+p(i) и попытаться разместить запись в этой позиции. При неудаче повторить шаг 3.

2. Процесс прекращается, если просмотрены все позиции таблицы, достижимые выбранным способом вычисления, и все они заняты. Необходимо пре­дупредить пользователя об отказе на запрос о включении новой записи.

3. Конец.

УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ

Основная литература

1. Хопкрофт Д., Ахо А., Ульман Д. Структуры данных и алгоритмы. – М.: Вильямс, 2009 – 384с.

2. Вирт Н. Алгоритмы и структуры данных. – СПб: Невский диалект, 2011 – 272с.

3. Бен-Ари. Языки программирования. Сравнительный анализ. - М.: Мир, 2009. 336с.

4. Мейер В., Бодуэн К. Методы программирования: В2т./Пер.с фр.Ю.А. Первина; Под ред. А.П. Ершова. - М.: Мир, 2007 - 336 с.

5. Бабушкина И.А. Практикум по ООП. М.-2009.

Дополнительная литература

1. Алгоритмы и программы. Сборник задач.- Чебоксары: изд-во «Клио», 2006.

2. Единая Система Программной Документации. Схемы алгоритмов и программ. Правила выполнения. ГОСТ 19.002-80.

3. Единая Система Программной Документации. Схемы алгоритмов и программ. Обозначения условные графические. ГОСТ 19.003-80

Задания и методические указания к выполнению

контрольной работы по дисциплине