Ориентированные графы

Ориентированный граф G - это пара (X, U), где X - множество элементов, называемых вершинами, a U - множество или набор различных упорядоченных пар (х, у), называемых дугами.

Пример

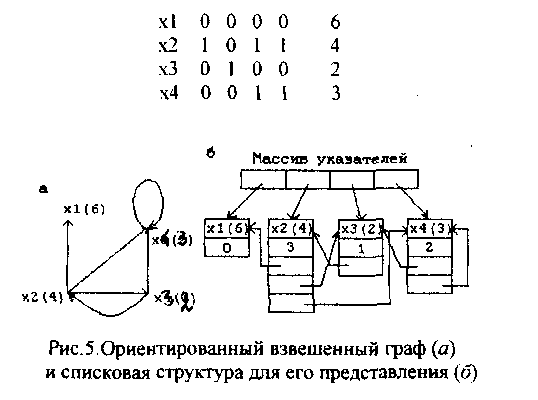
Взвешенный граф, изображенный на рис.5,а (в скобках указаны веса соответствующих вершин), может быть задан следующей матрицей смежности:

Из графического представления некоторого графа легко вывести пред­ставляющую его списковую структуру. Для каждой вершины графа построим следующий элемент:

Идентификатор вершин

Число дуг, выходящих из вершины n

Указатель на 1-ю вершину

Указатель на n–ю вершину

Используя эти элементы, можно построить списковую структуру для представления графа (рис. 5,б).

Деревья

Дерево - частный случай графа, поэтому для хранения дерева используют методы, которые применяют для графов. Но так как матрица смежности для графа сильно разряжена, для хранения дерева в памяти чаще применяют списковую форму представления.

Пример

Алгоритм построения дерева сортировки может быть задан следующим образом:

I. Начало. Предполагается, что выделена память для хранения списко­вой структуры, соответствующей дереву, которое будет построено в процессе сортировки. Элементы структуры имеют такой вид:

Левая отсылка

Информационное поле

Правая отсылка

Информационное поле содержит некоторый признак для сравнения элементов. Указатель на списковую структуру до применения алгоритма пуст.

2. Если поступил первый элемент сортируемого массива (это можно определить по пустому указателю списковой структуры), то он заносится в память: указатель принимает значение, равное отсылке на данный элемент (ко­рень формируемого дерева). Снимается копия указателя в поле, которое будем называть текущей отсылкой. Конец.

3. При поступлении очередного элемента сравнить его признак с приз­наком элемента, адресуемого текущей отсылкой. Если признак вновь посту­пившего элемента массива меньше, чем признак текущего элемента, и левая его отсылка не пуста, то ее следует перенести в поле текущей отсылки. Повторить шаг 3. Если левая отсылка пуста, то выполнить шаг 5.

4. Если признак вновь поступившего элемента больше или равен признаку текущего элемента, а правая отсылка не пуста, то перенести ее в поле те­кущей отсылки. Повторить шаг 3. Если правая отсылка пуста, то выполнить шаг 5.

5. Разместить новый элемент в списковой структуре, а левой (соответст­венно правой) отсылке текущего элемента, левая (правая) отсылка которого была пуста, присвоить значение, равное указателю на новый элемент.

6. Конец.

Пример

Поступает последовательность элементов со следующими числовыми признаками для сравнения: 5,3,7,8,1,2,4,9,6. Процесс формирования соответст­вующего дерева сортировки изображен на рис 6. Тот факт, что элемент с мень­шим значением признака перемещается влево, выбран случайно. Необходимо лишь, чтобы одинаковые результаты сравнений приводили к переходу в одном выбранном направлении.

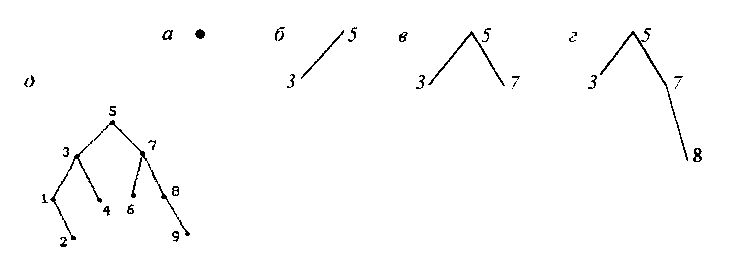
Рис.6. Построение дерева сортировки: а - поступил первый элемент; б - поступил второй элемент; в - поступил третий элемент; г - поступил четвертый элемент; д - окончательный результат

Существует два способа задания дерева; 1) таблица следов вершин (табл.5);

Таблица 5 - Таблица следов вершин

Вершина	След
Х0 Х1 Х2 Х3 Х4 …	1 10 11 100 101 …