Классификация систем автоматического управления.
В технике используется большое число САУ. Их можно классифицировать по различным признакам. По алгоритму функционирования САУ делятся на три группы:
1. Системы стабилизации. Предназначены для поддержания регулируемой величины на постоянном, заданном уровне (хрег = const);
2. Системы программного управления. Предназначены для изменения регулируемой величины в соответствии с определенным, заданным законом в виде функции от времени (Хрег =f(t));
3. Следящие системы. Предназначены для изменения регулируемой величины в виде функции некоторого параметра, закон изменения которого во времени неизвестен. Таким образом, алгоритм функционирования заранее неизвестен.
По наличию источнике энергии для передачи сигнала управления САУ можно разделить на две группы:
1. Системы прямого действия. В них используется энергия самого объекта управления, постороннего источника не требуется;
2. Системы непрямого действия. В них используется посторонний источник энергии: электрической, пневматический, гидравлический, смешанный.
По характеру протекания внутренних динамических процессов САУ делятся на три вида:
1. Непрерывные системы. Все элементы этих САУ являются непрерывными, то есть для каждого элемента непрерывному изменению входной величины соответствует непрерывное изменение выходной величины;
2. Дискретные системы. В дискретных САУ имеется хотя бы один элемент, в котором при непрерывном изменении входной величины выходная величина имеет вид импульсов, появляющихся через некоторые промежутки времени;
3. Системы релейного действия. В них имеется хотя бы один элемент, у которого при непрерывном изменении входной величины, выходная величина изменяется скачком и может принимать ограниченное число фиксированных значений;
По математическому описанию САУ можно разделить на две группы:
1. Линейные системы. Все элементы этих САУ, их динамика описываются линейными дифференциальными уравнениями;
2. Нелинейные системы. Под нелинейной понимают такую систему, в которой хотя бы одно звено описывается нелинейным уравнением .
Статические характеристики элементов сау.
Статические характеристики определяют функциональную связь между выходными и входными переменными элементов САУ, существующую установившихся значений координат. Статические характеристики не изменяются во времени и поэтому не содержат его, по виду статической характеристики элементы бывают статические и астатическими. Статическим называется такой элемент, у которого существует статическая характеристика в виде непрерывной, монотонной функции, т.е. когда каждому значению входной переменной соответствует единое значение входной величины рис.1.72.
а) линейный элемент a=arctgkx, где k-коэффициент усиления элемента.
б) нелинейный элемент
Ka=(dy/dx)
Рис.1.72. Функциональная связь между выходными и входными переменными элементами САУ.
Статический элемент называется линейным элементом, если график его статической характеристики близок прямой линии. Для большинства устройств статические характеристики отличаются от прямой линии. Подобные элементы называются нелинейными. Для них коэффициент усиления k величина переменная, зависящая от выбора координат рабочей точки на статической характе ристике. Деление элементов на линейные и нелинейные по виду их характеристик необходимо в связи с большим различием математического аппарата, применяемого для расчета линейных и нелинейных САУ.
Элементы, у которых отсутствует прямая связь между входной и выходной величинами в статическом режиме, а проявляется через производную называются статическими на рис.1.73.
а) Л.Э. AI, где dy/dx=bx
б) Н.Э. AI , гдеd2/dt2=cx
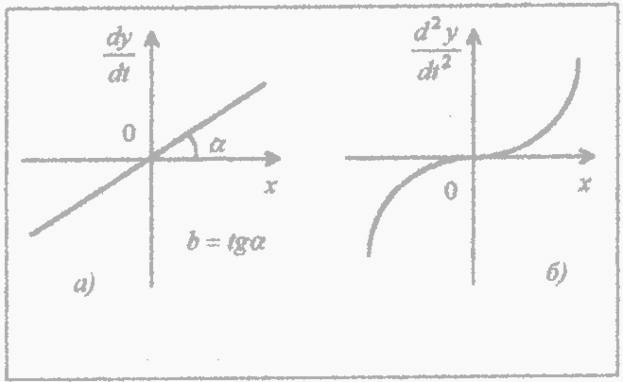
Рис 1.73. Функциональная связь между выходными и входными статическими элементами САУ
Примером такого устройства можно считать гидроцилиндр скорость движения поршня которого пропорциональна величине подачи (расходу рабочей жидкости). Для гидроцилиндра невозможно указать выходной координаты y, т.к. в уравнении присутствует скорость dy/dt перемещение поршня.
Порядок производной определяет порядок астатизма элемента. Коэффициенты b и c смысловые коэффициенты усиления по скорости и ускорению соответственно.