26.Теоремы ферма, ролля, лагранжа и коши

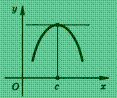
Теорема Ферма.  Если функция у = f (х),  определенная в интервале (а ; b), достигает в  некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует  производная f ′(с), то f ′(с) = 0.  

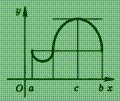
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).    Теорема Ролля. Если функция у = f (х),  непрерывная на отрезке [а ; b] и  дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.  Геометрически эта теорема означает  следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).    Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и  дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что   

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х)  между точками А и В найдется такая внутренняя точкаС, что касательная к графику в точке С параллельна хорде АВ.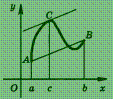   

Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.  

Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];  

2)  дифференцируемы в интервале (а ; b);  

3) g'(x) ≠ 0 в этом  интервале,  

то в интервале (а ; b) существует  такая точка с, что имеет место равенство 

 

Раскрытие неопределенностей. Правило Лопиталя

27. Раскрытие неопределенностей. Правило Лопиталя

1. Неопределенность вида 0/0. Первое правило Лопиталя .

Если   = 0, то  , когда последний существует.

2. Неопределенность вида / . Второе правило Лопиталя .

Если   = , то  , когда последний существует.

3. Неопределенности вида 0 , - , 1 ^и 0 ⁰ сводятся к неопределенностям 0/0 и / путем алгебраических преобразований.

Пример 3.25. Найти предел функции y =   при x 0.

Решение. Имеем неопределенность вида - . Сначала преобразуем ее к неопределенности вида 0/0, для чего достаточно привести дроби к общему знаменателю. К полученному выражению два раза применим правилоЛопиталя . Записывая последовательно все промежуточные вычисления, будем иметь :

 =   =   =   =  =   =  .

Пример 3.26 . Найти  .

Решение. Раскрывая неопределенность вида / по правилу Лопиталя , получаем:

  =   =   =0.

Пример 3.27 . Вычислить  .

Решение. Имеем неопределенность вида 1 ^. Обозначим искомый предел через A. A =  .

Тогда ln A =   =   =   = 2, 

28.Понятие экстремума функции

Определение

Точка   называется точкой локального максимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности выполняется неравенство:  .

Точка   называется точкой локального минимума функции  , если существует такая окрестность этой точки, что для всех   из этой окрестности  .

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка   называется точкой строгого локального максимума функции  , если для всех   из окрестности этой точки будет справедливо строгое неравенство  .

Точка   называется точкой строгого локального минимума функции  , если для всех   из окрестности этой точки будет справедливо строгое неравенство  .

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.