Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Ярославский государственный технический университет»

Кафедра кибернетики

Отчет защищен

с оценкой

Преподаватель

к. т. н., доцент

Н.Н. Василькова

дата

Исследование методов вычислений в математическом моделировании

Отчет по расчетно-графической работе

по дисциплине «Компьютерные технологии вычислений в математическом моделировании»

КТВММ 0204.220301.022.РГР

Отчет выполнил

студент гр. МА-33

Д.Н. Петровский

дата

2005

1. Выполнение практического задания.

Задание 1.1.

1. Используя заданную функцию f(x) = 1.5х+8sin(1.5х+2), рассчитать 5 точек в интервале [-5; 1.25], которые использовать как узлы интерполяции. Выбрать точку х внутри этого интервала, в которой восстановить значение функции с помощью метода Сплайнов. Найти погрешность интерполяции путём сравнения полученного значения и рассчитанного по f(x).

Решение

1. Рассчитаем 5 точек.

2. Для каждого из подинтервалов найдем коэффициенты кубического сплайна.

Составим и решим систему уравнений.

3. Примем х=-1 и восстановим значение функции.

4. Найдем погрешность интерполяции.

f(-1) = 1.5∙-1+8sin(1.5∙-1+2)= 2.335

Задание 1.2.

Используя полученные на предыдущем этапе точки построить аппроксимирующие полиномы второго порядка: y = d₂x² + d₁x+d₀, методом наименьших квадратов при всех одинаковых весовых коэффициентах и при весовом коэффициенте в третьей точке в 3 раза большем, чем в остальных. Получить среднеквадратичную погрешность критерия близости и расчетное значение y в третьей точке.

Решение

1. b₁= b₂= b₃=1

,

где .

Из условия минимума.

Уравнение аппроксимирующей функции:

xi	-5	-3.4375	-1.875	0.3125	1.25
yi	-1.856	-5.039	-8.621	5.454	-3.48
yiрасч	-12.986	-6.36	-1.316	3.088	4.027

Квадратичный критерий близости:

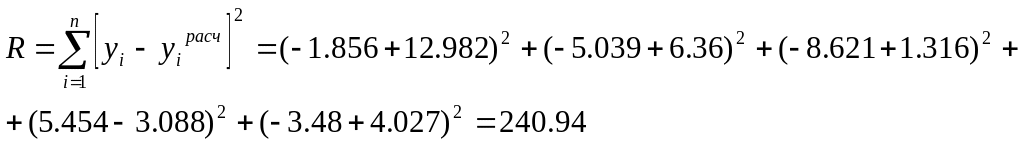
Среднеквадратичная погрешность аппроксимации:

2. b₁= b₂= 1, b₃=3

Уравнение аппроксимирующей функции:

xi	-5	-3.4375	-1.875	0.3125	1.25
yi	-1.856	-5.039	-8.621	5.454	-3.48
yiрасч	-2.272	-6.216	-6.956	-2.612	1.172

Квадратичный критерий близости:

Среднеквадратичная погрешность аппроксимации:

3. Расчётное значение «у» в третьей точке, т.е. х = -1.875:

	При первой аппроксим. функц.	При второй аппроксим. функц.
y	-1.316	-6.956