Поточные криптосистемы. Принципы построения. Классификация. Проблема синхронизации.
Потоковый шифр при каждом шифровании превращает один и тот же бит или байт открытого текста в различные биты или байты шифротекста.
Простейшая реализация (режим гаммирования).
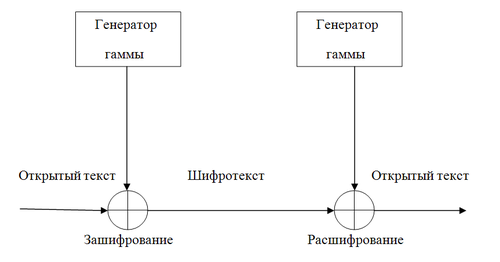
Простейшая
реализация поточного шифра изображена
на рисунке. Генератор гаммы выдаёт
ключевой поток (гамму): 
.
Обозначим поток битов открытого текста 
.
Тогда поток битов шифротекста получается
с помощью применения операции XOR: 
,
где 
.
Расшифрование
производится операцией XOR между той же
самой гаммой и зашифрованным текстом: 
.
Классификация:
самосинхронизирующиеся
cинхронные.
Проблемы:
-Если один из генераторов пропустил цикл или один бит при передаче был потерян, то необходима синхронизация
-уязвимы к изменению отдельных бит шифрованного текста. Если злоумышленнику -известен открытый текст, он может изменить эти биты так, чтобы они расшифровывались, как ему надо.
Линейные конгруэнтные генераторы. Линейные регистры сдвига.
Имеют вид
Xn = (aXn-1+b) mod m
a, b, m – постоянные (множитель, инкремент и модуль).
Ключом служит X0
Период не больше, чем m.
Параметры подбираются, чтобы иметь генератор с максимальным периодом.
Быстрота за счет малого количества операций на бит.
Предсказуемы.
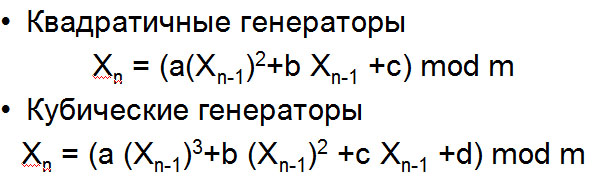
Простейшим видом сдвигового регистра с обратной связью является линейный сдвиговый регистр с обратной связью (Linear feedback Shift Register, или LFSR). Обратная связь представляет собой XOR некоторых битов регистра.
LFSR
чаще других сдвиговых регистров
используются в криптографии.
В качестве примера рассмотрим 4 - битовый LFSR c отводом от первого и четвёртого битов:
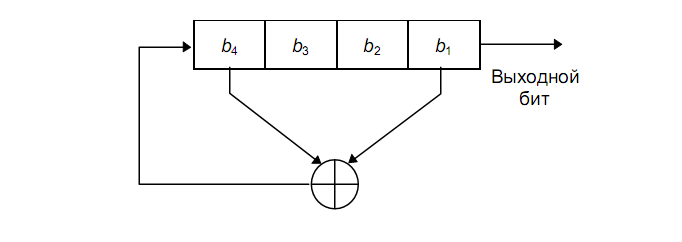
1111
0111
1011
0101
1010
1101
0110
0011
...
Выходной последовательностью будет строка младших значащих битов:1,1,1,1,0,1,0,1,....
Поточные шифры. Отличия от блочных. Стойкость. Методы анализа.
Потоковый шифр при каждом шифровании превращает один и тот же бит или байт открытого текста в различные биты или байты шифротекста.
Простейшая реализация.
Генератор потока ключей выдаёт поток битов:
k1,k2,....,kn.
Этот поток ключей и поток битов открытого текста
p1, p2, p3,.....,pn
подвергаются операции XOR
в результате получается поток битов шифротекста.
Ci=Pi xor Ki
при расшифровании
Pi = Ci xor Ki.
Примеры поточных шифров на основе lfsr.
Большинство реальных потоковых шифров построены на LFSR. Проблема состоит в том, что программная реализация таких шифров очень неэффективна.
Сдвиговый регистр с обратной связью состоит из двух частей: сдвигового регистра и функции обратной связи.
Сдвиговый регистр представляет собой последовательность битов. Когда нужно извлечь бит, все биты сдвигового регистра сдвигаются вправо на 1 позицию.
Новый крайний левый бит является значением функции обратной связи от остальных битов регистра.
Периодом сдвигового регистра называется длина получаемой последовательности до начала её повторения.
Если функция обратной связи зависит от малого числа битов регистра, то шифр может терять безопасность; если при вычислении функции обратной связи задействовано много битов, то реализация становится неэффективной.
Важным параметром, используемым для анализа генераторов на базе LFSR, является линейная сложность. Она определяется как длина n самого короткого LFSR, который может имитировать выход генератора. Любая последовательность, генерированная конечным автоматом над конечным полем, имеет конечную линейную сложность.
Высокая линейная сложность не обязательно гарантирует безопасность генератора, но низкая линейная сложность указывает на недостаточную безопасность генератора.
Опасность состоит в том, что одна или несколько внутренних выходных последовательностей (часто просто выходы отдельных LFSR) могут быть связаны общим ключевым потоком и вскрыты при помощи линейной алгебры.
Такое понятие называют корреляционным вскрытием. Томас Сигенталер показал, что можно точно определить корреляционную независимость, и что существует компромисс между корреляционной независимостью и линейной сложностью.
Основной идеей корреляционного вскрытия является обнаружение некоторой корреляции между выходом генератора и выходом одной из его составных частей. Тогда, наблюдая выходную последовательность, можно получить информацию об этом промежуточном коде.
Используя эту информацию и другие корреляции, можно собирать данные о других промежуточных выходах до тех пор, пока генератор не будет взломан.
Примеры потоковых шифров на базе LFSR
Основной подход при проектировании генератора потока ключей.
Сначала берётся один или несколько LFSR, обычно с различными длинами и различными многочленами обратной связи.
Ключ является начальным состоянием регистров LFSR.
Каждый раз, когда необходим новый бит, сдвигаем на бит регистры LFSR (тактирование - clocking).
Бит выхода представляет собой функцию, лучше нелинейную, некоторых битов регистров LFSR. Эта функция называется комбинирующей функцией, а генератор в целом комбинационным генератором.
Усложнения. В некоторых генераторах для различных LFSR используется различная тактовая частота. Управление тактовой частотой может быть с прямой связью, когда выход одного LFSR управляет выходом другого LFSR, или с обратной связью, когда выход одного L FSR управляет его собственно тактовой частотой.