- •Виды атак на криптографические алгоритмы. Понятие стойкости.
- •Шифры замены. Математическая модель. Примеры.
- •Шифры перестановки. Математическая модель. Примеры.
- •Шифры гаммирования. Математическая модель. Примеры.
- •Принципы построения блочных шифров. Схема Фейстеля.
- •Шифрование в ячейке Фейстеля Расшифрование в ячейке Фейстеля Формирование группы
- •Алгоритм симметричного шифрования des.
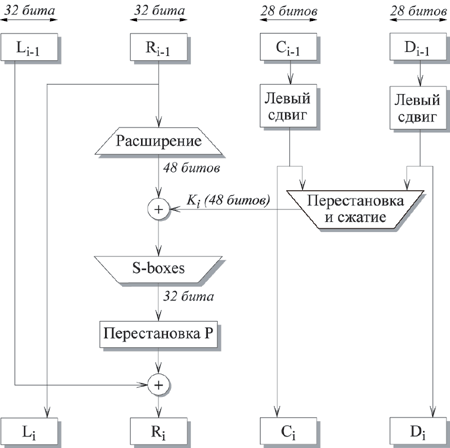
- •Алгоритм симметричного шифрования гост 28147-99.
- •Алгоритм симметричного шифрования Rijndael.
- •4.Добавление ключа.
- •Алгоритмы симметричного шифрования idea и Blowfish.
- •Режимы выполнения алгоритмов симметричного шифрования.
- •Поточные криптосистемы. Принципы построения. Классификация. Проблема синхронизации.
- •Линейные конгруэнтные генераторы. Линейные регистры сдвига.
- •Поточные шифры. Отличия от блочных. Стойкость. Методы анализа.
- •Примеры поточных шифров на основе lfsr.
- •Примеры поточных шифров, использующих аддитивные генераторы:
- •Примеры поточных шифров на основе fcsr.
- •Математические методы криптоанализа: метод опробывания, методы на основе теории статистических решений.
- •Линейный криптоанализ.
- •Разностный криптоанализ.
- •Атаки на функции хэширования.
- •Функция хеширования md5.
- •Функция хеширования sha-1.
- •Функция хеширования гост 3411-94.
- •Функция хеширования стб 1176.1-99.
- •Общие положения электронной цифровой подписи. Задачи. Требования.
- •Прямая и арбитражная цифровая подписи. Примеры.
- •Стандарт электронной цифровой подписи dss.
- •Цифровая подпись на основе алгоритмов с открытыми ключами. Схема Фиата-Шамира.
- •Цифровая подпись Эль-Гамаля. Схема rsa.
- •Стандарт электронной цифровой подписи dss.
- •Стандарт электронной цифровой подписи гост-р 34.10-94.
- •Стандарт электронной цифровой подписи стб 1176.2-99.
- •Применение эллиптических кривых в криптографии. Алгоритм шифрования на основе эллиптических кривых.
- •Алгоритмы обмена ключами и электронной цифровой подписи на основе эллиптических кривых.
- •Стеганографические методы защиты информации. Основные понятия и определения. Области применения.
- •Общая модель стеганосистемы. Проблема устойчивости. Стегоанализ.
- •Методы сокрытия информации в неподвижных изображениях.
- •Методы сокрытия информации в текстовых данных.
- •Протоколы аутентификации. Двусторонняя аутентификация.
- •Протоколы аутентификации. Односторонняя аутентификация.
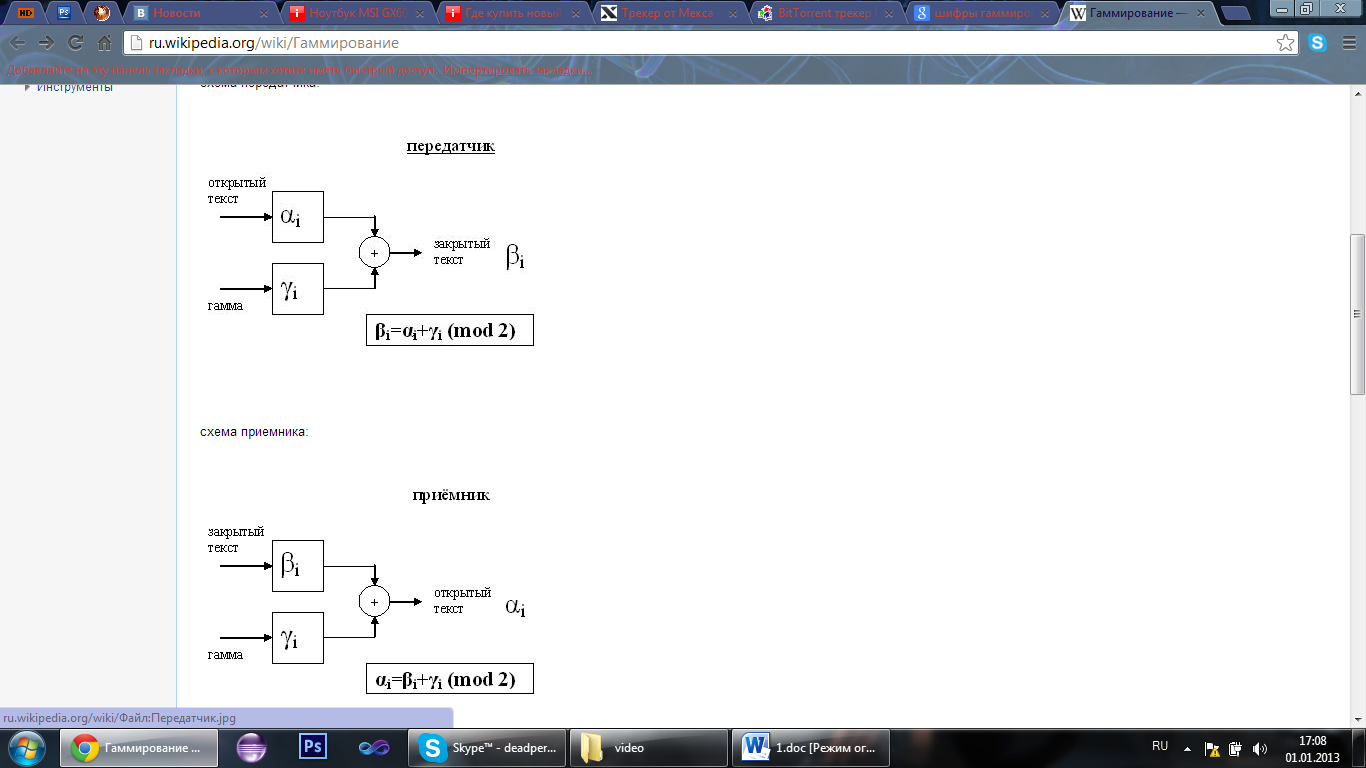
Шифры гаммирования. Математическая модель. Примеры.
Гамми́рование — симметричный метод шифрования, основанный на «наложении» гамма-последовательности на открытый текст. Обычно это суммирование в каком-либо конечном поле
Принцип шифрования заключается в формировании генератором псевдослучайных чисел (ГПСЧ) гаммы шифра и наложении этой гаммы на открытые данные обратимым образом, например путем сложения по модулю два. Процесс дешифрования данных сводится к повторной генерации гаммы шифра и наложении гаммы на зашифрованные данные. Ключом шифрования в данном случае является начальное состояние генератора псевдослучайных чисел. При одном и том же начальном состоянии ГПСЧ будет формировать одни и те же псевдослучайные последовательности.
Принципы построения блочных шифров. Схема Фейстеля.
С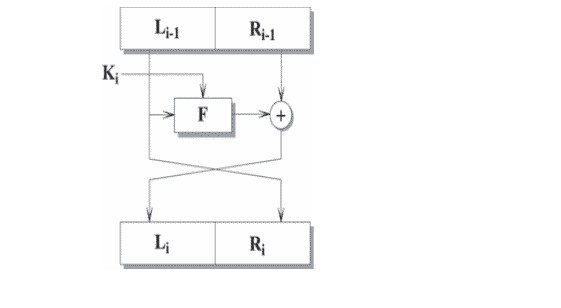 еть
Фейстеля:
еть
Фейстеля:
Сеть Фейстеля — это общий метод преобразования произвольной функции F в перестановку на множестве блоков. [15] Она состоит из циклически повторяющихся ячеек — раундов. Внутри каждого раунда блок открытого текста разделяется на две равные части. Раундовая функция
![]()
берет одну половину (на рис. правую), преобразует её с использованием ключа Ki и объединяет результат с второй половиной посредством операции исключающее ИЛИ (XOR). Этот ключ задаётся первоначальным ключом K и различен для каждого раунда. Далее половинки меняются местами (иначе будет преобразовываться только одна половина блока) и подаются на следующий раунд. Преобразование сети Фейстеля является обратимой операцией.
Для функции F существуют определенные требования:
её работа должна приводить к лавинному эффекту
должна быть нелинейна по отношению к операции XOR
В случае невыполнения первого требования, сеть будет подвержена дифференциальным атакам (похожие сообщения будут иметь похожие шифры). Во втором случае действия шифра линейны и для взлома достаточно решения системы линейных уравнений. [3]
Подобная конструкция обладает ощутимым преимуществом: процедурышифрования/расшифрования совпадают, только производные от первоначального ключи используются в обратном порядке. Это значит, что одни и те же блоки могут использоваться как для шифрования, так и для расшифрования, что, безусловно, упрощает реализацию шифра. Недостаток схемы заключается в том, что в каждом раунде обрабатывается только половина блока, что приводит к необходимости увеличивать число раундов. [2]
Шифрование в ячейке Фейстеля Расшифрование в ячейке Фейстеля Формирование группы
При построении алгоритма учитывают формирование группы, в которой элементами являются множество блоков шифротекста при всех ключах, а групповой операцией — композиция раундов шифрования. Если данный шифр образует практически полную группу, не имеет смысла применять кратное шифрование.
Алгоритм симметричного шифрования des.
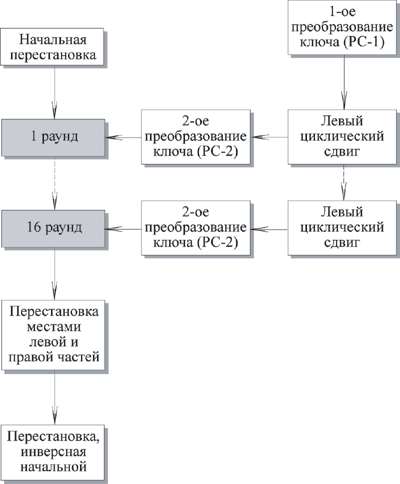
1-ый раунд DES