Предмет криптографии. Определения. Задачи. Исторические примеры.
Криптология – это наука, состоящая из двух ветвей, цели которых прямо противоположны:
Криптография – наука о способах преобразования (шифрования) информации с целью обеспечения ее секретности, аутентичности и неотслеживаемости.
Криптоанализ – о методах и способах оценки надежности, анализа стойкости и разработки способов вскрытия шифров.
Основные задачи:
Обеспечение конфиденциальности.
Обеспечение целостности.
Обеспечение аутентификации.
Обеспечение невозможности отказа от авторства
Шифр – семейство обратимых преобразований, каждое из которых определяется некоторым параметром, называемым ключом, а также порядком применения данного преобразования, называемого режимом шифрования.
Ключ представляет собой буквенную или числовую последовательность.
Любое преобразование однозначно определяется ключом и описывается некоторым криптографическим алгоритмом.
Пару алгоритмов зашифрования и расшифрования называют криптосистемой (шифросистемой), а реализующие их устройства – шифротехникой.
Обозначим:
M – открытое сообщение, С – шифрованное сообщение.
Зашифрование алгоритмом E с ключом k1 означает, что
Ek1(M) = C
Расшифрование алгоритмом D с ключом k2
Dk2(C) = M
Алгоритмы должны удовлетворять равенству
Dk2(Ek1(M)) = M
Зашифровка – процесс преобразования множества открытого сообщения в множество закрытое сообщение.
Дешифрование – процесс нахождения открытого сообщения, соответствующему заданному закрытому сообщению при неизвестном криптопреобразовании.
Абстрактно систему можно описать как множество открытых сообщений в множество закрытых. Выбор конкретного типа преобразования определяется ключом расшифрования.
Отображения должны быть взаимно однозначные.
Ключи зашифрования и расшифрования могут быть различны.
Множество, из которых выбираются ключи, называется ключевым пространством.
Совокупность процессов зашифрования, множества открытых сообщений, множества возможных закрытых сообщений и ключ пространства называется алгоритмом зашифрования.
Исторические примеры. Около 4000 лет назад египтяне заменяли иероглифы в важных местах на другие.Но их было не трудно расшифровать,видимо цель была не в этом. Скиталы – кожаная полоска наматывается на цилиндр определенной толщины. Диск Энея( 4 век до н.э.) на диске просверливаются дырки, соотв.буквам, через них продевается в нужном порядке нить. Расшифровка тривиальна, но сообщение можно мгновенно уничтожить. Он же книжный шифр: незаметные пометки над буквами книги ( первая стеганография)
Квадрат Полибия: в квадрат вписываются буквы, каждая буква заменяется на ту, что под ней. Шифр – порядок букв в этом квадрате. Геродот упоминает, как сообшение о планирующейся атаке персов было записано на основе восковых табличек,которые потом опять покрыли воском. Шифр Цезаря – простой шифр подстановки. Буквы сдвигаются на фиксированное число позиций. A-D, B-E.... Талмуд – атбаш: первая буква заменяется на последнюю. Вторая на предпоследнюю… Шифр Цезаря и атбаш – частные случаи моноалфавитных шифров (в них в каждой букве становится в соответствие другая бука алфавита). Полиалфавитные шифры : первый такой шифр: диск. Внутри код. Снаружи сообщение. Время от времени сдвигаем внутренний диск, изменяя тем самым код. Иоганн Трисемус, 1508 «Полиграфия» - первый труд по криптографии. Шифр Трисемуса – квадрат, tabula recta, в котором записан алфавит со смещением. Первая буква кодируется по первой строке и т.д.
Блез де Виженер, 1586 – предложил кодировать сообщение им самим: первая расшифрованная буква используется для декодирования второй и т.д. Многое изменилось после изобретения телеграфа. Нужно было кодировать большие объемы сообщений. Прежние шифры были слишком трудоемки. Перешли на простые коды, секретность достигалась частой сменой кодовых слов. Были и новые шифры. Цилиндр Джеферсона: чтобы зашифровать, нужно повернуть цилиндры так, чтобы получилось сообщение и записать какую-нибудь другую строчку, чтобы дешифровать нужно повернуть цилиндры так, чтобы получился код и поискать ту строчку, которая имеет смысл как сообщение. Во время мировых войн на криптографию сильно повлияло радио. Теперь перехватывали большое количество вражеских сообщений.
В
1910-е годы Гильберт Вернам :
улучшил
шифр Виженера;
разработал шифр,
который невозможно взломать. Одноразовый
блокнот: используем одноразовый секретный
ключ k, который просто
побитово складывался с сообщением:
Без
знаний о ключе и сообщении враг,
перехвативший сообщение, получил ровно
ноль информации.
Whitfield
Diffie, Martin Hellman, 1976, “New directions in cryptography” –
протокол согласования
ключа Диффи-хелмана.
Ron
Rivers, Adi Shamir,Leonard Adleman, 1978 – RSA, первая
криптосистема с
открытым ключом.
Виды атак на криптографические алгоритмы. Понятие стойкости.
Криптоатака с использованием только шифрованных текстов.
Криптоатака с использованием открытых текстов и соответствующих им шифрованных текстов.
Криптоатака с использованием выбираемых криптоаналитиком открытых текстов и соответствующих им шифрованных.
Криптоатака с использованием активного аппарата воздействия на систему
Стойкость алгоритмов шифрования
Под раскрытием понимаем:
Полное – нашел ключ.
Нахождение эквивалентного алгоритма – не имея представления о ключе.
Раскрытие открытого сообщения – вычислил 1, соответствующее 1 из зашифрованных.
Частичное раскрытие – частичные сведения о ключе.
Факторы, влияющие на раскрытие шифра:
объем сообщений;
время для вычислений;
вычислительные ресурсы.
Стойким считается алгоритм, который для своего раскрытия требует практически недостижимых вычислений ресурсов, или недостаток времени, или недостаток объема.
!!Любой алгоритм может быть вскрыт прямым перебором.
Классификация алгоритмов шифрования. Примеры простейших шифров.
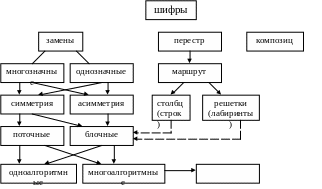
Или другой вариант:
ШИФРЫ
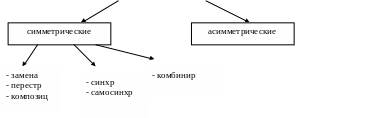
Шифры перестановки
Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки.
Р
ассмотрим,
предназначенное для зашифрования
сообщения длиной n
символов. Его можно представить с помощью
таблицы
где i1 - номер места шифртекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании, i2 - номер места для второй буквы и т.д.
В верхней строке таблицы выписаны по порядку числа от 1 до , а в нижней - те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени n. Зная подстановку, задающую преобразование, можно осуществить как зашифрование, так и расшифрование текста.
Маршрутная перестановка
Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного ``маршрута'', а затем по ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой.
Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево.
Выписывать сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.
При расшифровании надо определить число длинных столбцов, т.е. число букв в последней строке прямоугольника. Для этого нужно разделить число буев в сообщении на длину числового ключа. Остаток от деления и будет искомым числом.
Шифр ``Сцитала''.
Одним из самых первых шифровальных приспособлений был жезл (``Сцитала''), применявшийся еще во времена войны Спарты против Афин в V веке до н. э.
Это был цилиндр, на который виток к витку наматывалась узкая папирусная лента (без просветов и нахлестов), а затем на этой ленте вдоль его оси записывался необходимый для передачи текст. Лента сматывалась с цилиндра и отправлялась адресату, который, имея цилиндр точно такого же диаметра, наматывал ленту на него и прочитывал сообщение. Ясно, что такой способ шифрования осуществляет перестановку местами букв сообщения.
Шифр ``Сцитала'‘ реализует не более n перестановок (n - длина сообщения).
Действительно, этот шифр, как нетрудно видеть, эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из столбцов, построчно записывают сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.
Имеются еще и чисто физические ограничения, накладываемые реализацией шифра ``Сцитала''. Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 1 сантиметр на одном витке такого жезла уместится не более 32 букв (10p < 32 ). Таким образом, число перестановок, реализуемых ``Сциталой'', вряд ли превосходит 32.
Шифр ``Поворотная решетка''.
Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера клеток.
В трафарете вырезано 2m x 2k клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.
