20.Либрация луны. Физическая и оптическая либрации.

В каждый данный момент с Земли видна ровно половина поверхности Луны, но продолжительные наблюдения позволяют изучать почти 60% ее поверхности. Это возможно благодаря явлениям, носящим общее название либрации (качаний) Луны.

Оптические, или видимые либрации, при которых Луна в действительности никаких “колебаний” не совершает, бывают трех видов: по долготе, по широте и параллактическая.

Либрация по долготе вызывается тем, что Луна вращается вокруг оси равномерно, а ее движение по орбите согласно второму закону Кеплера вблизи перигея быстрее, а вблизи апогея — медленнее. Поэтому за четверть месяца после прохождения перигея П (рис. 57) Луна пройдет путь больше четверти всей орбиты, а вокруг оси повернется ровно на 90°. Точка а, которая ранее была в центре лунного диска, теперь будет видна уже левее центра диска (сместится к востоку).

 

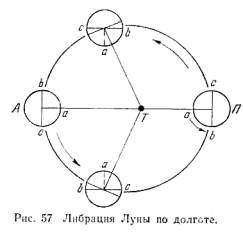
В том же направлении сместится и точка b, которая раньше была видна на правом (западном) краю диска, и, следовательно, станет видимой часть поверхности Луны за западным краем ее диска. В апогее А будет видна та же поверхность Луны, что и в перигее, но за четверть месяца после прохождения апогея Луна пройдет меньше четверти всей орбиты, а вокруг оси снова повернется ровно на 90°, и теперь уже будет видна  часть  поверхности Луны за восточным краем ее диска. Период либрации по долготе равен аномалистическому месяцу, а наибольшая возможная величина ее 7° 54'.

Либрация по широте возникает от наклона оси вращения Луны к плоскости ее орбиты и сохранения направления оси в пространстве при движении Луны (рис. 58).

 

 

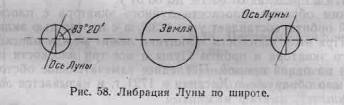
В результате с Земли попеременно видна то часть поверхности Луны, расположенная вокруг ее южного полюса, то, наоборот, вокруг северного полюса. Период либрации по широте равен драконическому месяцу, а ее величина достигает 6°50’.

Суточная или параллактическая либрация возникает вследствие сравнительной близости Луны к Земле. Поэтому из разных точек Земли поверхность Луны видна неодинаково. Два наблюдателя, находящиеся в двух противоположных точках земного экватора, в один и тот же момент видят несколько различные области лунной поверхности. Так, наблюдатель, для которого Луна только еще восходит, видит часть поверхности Луны за ее западным краем диска, а второй наблюдатель, для которого Луна в этот момент уже заходит, этой части поверхности Луны не видит, но зато видит часть поверхности за восточным краем диска. Параллактическая либрация составляет около 1°.

Физическая либрация, т.е. действительное “качание” Луны, происходит оттого, что большая полуось лунного эллипсоида периодически отклоняется от направления на Землю, а притяжение Земли стремится вернуть ее в это положение. Величина физической либрации очень мала — около 2".

 

21. Закон всемирного тяготения - основа небесной механики и космонавтики .

Анализируя законы Кеплера и наблюдательные данные о движении Луны, Ньютон сформулировал новый закон: каждая частица вещества притягивается к любой другой частице вдоль соединяющей их прямой с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.  Это всеобщий закон; он не ограничен влиянием Солнца на планеты. Он описывает также взаимодействие двух звезд, планеты и ее спутника, Земли и метеорита, Солнца и кометы. Все вещество во Вселенной подчиняется этому закону, поэтому его называют закономвсемирного тяготения. Всеобщность этого закона дополняется его уникальностью: как доказали математики, планетные орбиты имеют вид эллипсов, в фокусе которых находится Солнце, только в том случае, если притяжение меняется обратно пропорционально квадрату расстояния.  Казалось бы, попытка на основе ньютоновых законов движения и гравитации исследовать относительное движение взаимно притягивающихся тел должна привести к выводу знакомых нам законов Кеплера. Но это решительно не так, ибо законы Кеплера справедливы только в том случае, если:  1) взаимодействуют не более двух тел;  2) тела движутся по замкнутым орбитам;  3) масса одного из тел пренебрежимо мала по сравнению с массой другого.  Эти условия делают анализ предельно простым, но они совершенно не обязательны для применения законов движения и гравитации. Используя эти общие законы, мы можем пренебречь указанными ограничениями. Сделаем это, отказываясь каждый раз лишь от одного из них.  Во-первых, можно показать, что орбита может быть не только эллипсом (частный случай которого - окружность), но также параболой или гиперболой. Все эти кривые называют "коническими сечениями", поскольку они получаются при пересечении прямого кругового конуса плоскостью. Круг и эллипс - замкнутые кривые; парабола и гипербола - незамкнутые. Спутник, движущийся по замкнутой орбите, совершает одинаковые обороты снова и снова, а спутник, движущийся по незамкнутой кривой, приближается к главному телу с бесконечно далекого расстояния и, пролетев поблизости от него, вновь удаляется на бесконечность.  Во-вторых, можно показать, что "постоянная" величина a3/P2 в гармоническом законечисленно равна сумме масс двух взаимодействующих тел, если a выражено в расстояниях Земли от Солнца (в астрономических единицах), P - в периодах обращения Земли (в годах), а масса - в сумме масс Земли и Солнца. Поскольку в Солнечной системе масса любой планеты не превосходит тысячной доли массы Солнца, величины a3/P2 для всех планет различаются не более чем на 0,1%. Будь планеты массивнее, Кеплер не смог бы сформулировать свой гармонический закон. В общем виде этот закон выглядит так:  a3/P2 = M+m где M и m - массы компонентов системы, например Земли и Луны или звезд в двойной системе, причем значения масс могут быть любыми. (Все значения величин в этой формуле должны быть выражены в единой системе, например: астрономическая единица, год, масса Солнца.) Этот закон астрономы используют для определения масс различных космических объектов.  Можно также исследовать поведение трех или более взаимно притягивающихся тел. Закон тяготения позволяет вычислить силу, действующую на каждое из тел со стороны остальных, а законы движения - определить, как изменяется от этого его скорость. В случае двух тел их траектории движения могут быть представлены простыми уравнениями Кеплера. Но если тел больше, то это невозможно сделать с помощью конечного числа уравнений. 

Небе́сная меха́ника — раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны ипланет, предсказанием места и времени затмений, в общем, определением реального движения космических тел.

Задача небесной механики состоит в том, чтобы определить действующую на небесное тело силу гравитации и выяснить, как она влияет на его движение.

Задача двух тел

В классической механике, задача двух тел состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Распространённые примеры включают спутник, обращающийся вокруг планеты, планета, обращающаяся вокруг звезды, две звезды, обращающиеся вокруг друг друга (двойная звезда), и классический электрон, движущийся вокруг атомного ядра.

Задачу двух тел можно представить как две независимых задачи одного тела, которые привлекают решение для движения одной частицы во внешнем потенциале. Так как многие задачи с одним телом могут быть решены точно, соответствующая задача с двумя телами также может быть решена. В отличие от этого, задача с тремя телами (и, более широко, задача n тел) не может быть решена, кроме специальных случаев.

Постановка задачи 

Пусть   и   радиус-векторы двух тел, а   и   их массы. Наша цель определить траектории   и   для любого времени  , при заданных начальных координатах

, 

и скоростях

,  .

Второй закон Ньютона применительно к данной системе утверждает, что

где

 — сила действующая на первое тело из-за взаимодействием со вторым телом, и

 — сила действующая на второе тело со стороны первого.

Складывая и вычитая эти два уравнения, можно разделить одну задачу на две задачи с одним телом, которые могут быть решены независимо. "Сложение" уравнений (1) и (2) приводит к уравнению, описывающему движение центра масс . В отличие от этого, "вычитание" уравнения (2) из уравнения (1) приводит к уравнению, которое описывает, как вектор  между массами изменяется со временем. Решение этих независимых задач может помочь в нахождении траекторий   и  .

Движение центра масс (первая задача) 

Сложение уравнений (1) и (2) приводит к равенству

где мы использовали третий закон Ньютона   и где

позиция центра масс системы. Уравнение в итоге запишется в виде

Оно показывает, что скорость   центра масс постоянна. Отсюда следует, что полный момент количества движения   также сохраняется (сохранение импульса). Позиция и скорость центра масс может быть получена в любой момент времени.

Движения вектора смещения (вторая задача) 

Вычитая уравнение (2) из уравнения (1) и преобразуя приходим к уравнению

где мы снова использовали третий закон Ньютона   и где   (определённый выше) - вектор смещения, направленный от второго тела к первому.

Сила между двумя телами должна быть функцией только   а не абсолютных положений   и  ; в противном случае задача не имеет трансляционной симметрии, то есть законы физики менялись бы от точки к точке. Таким образом можно записать:

где   -приведённая масса

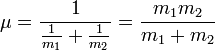
Как только мы найдём решение для   и  , первоначальные траектории можно записать в виде

как может быть показано подстановкой в уравнения для   и  .

Решение задачи двух тел 

Согласно третьему закону Ньютона силы, с которыми тела действуют друг на друга, равны по величине и противоположны по направлению. Таким образом, для задачи двух тел можно записать

Проинтегрировав это уравнение два раза, получим

где a и b – некоторые векторы.

Обозначив через r и M координату центра тяжести двух тел и их суммарную массу соответственно

получим

то есть центр масс системы движется с постоянной скоростью.

Запишем силы, действующие на каждое из тел, следующим образом

     где     

Вычитая второе уравнение из первого, получим

     где     

Векторно умножая последнее уравнение на r и интегрируя, получим

Постоянный вектор h, являющийся постоянной интегрирования, называется кинетическим моментом системы. Взаимное движение тел происходит в плоскости, перпендикулярной этому вектору. Введём систему цилиндрических координат r, ?, z. Единичные векторы вдоль радиальной, трансверсальной и вертикальной оси обозначим как i, j и k. Проекции скорости на радиальную и трансверсальную оси составят Тогда

левой части последнего выражения стоит удвоенная площадь треугольника, описываемого радиус-вектором r за единицу времен. Таким образом, это соотношение является математической записью второго закона Кеплера. Уравнение(1) умножаем скалярно на скорость и интегрируем

Движение двух тел в плоскости 

Замечательно, что движение двух тел всегда происходит в плоскости. Определим линейный импульс   и угловой момент

Скорость изменения углового момента равна моменту силы 

однако законы движения Ньютона выполняются для всех физических сил, и гласят, что сила, действующая между двумя частицами (материальными точками) направлена по линии соединяющей их положения, то есть . Отсюда и угловой момент сохраняется. тогда вектор смещения и его скорость лежат в плоскости перпендикулярной постоянному вектору .

Общее решение для силы, зависящей от расстояния 

Часто полезно перейти в полярные координаты, поскольку движение происходит в плоскости и для многих физических задач сила   является функцией радиуса   (центральные силы). Поскольку r-компонента ускорения равняется  , уравнение для r-компоненты вектора смещения   можно переписать в виде

где   и угловой момент   сохраняется. сохранение углового момента позволят найти решение для траектории   используя замену переменных. Переходя от   к 

получим уравнение движения

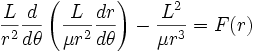
Это уравнение становится квазилинейным при замене переменных   и умножение обоих частей уравнения на 

Применение 

Для сил   обратно пропорциональных квадрату расстояния, таких как гравитация илиэлектростатика в классической физике получим

для некоторых констант  , уравнение для траекторий становится линейным

Решение этого уравнения

где   и   константы. Это решение показывает, что орбита представляет собойконическое сечение, то есть эллипс, гиперболу или параболу, в зависимости от того меньше  выражения  , больше или равно.

Движение тела в центральном теле

Орбитальная скорость тела (обычно планеты,естественного или искусственного спутника, кратной звезды) — это скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.

Определение 

В полярных координатах выражение для орбитальной скорости ( ) при кеплеровском движении поконическому сечению (эллипсу, параболе илигиперболе) имеет следующий вид[:

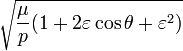
где:

 — гравитационный параметр, равный G(M+m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела

 — фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение   — для эллипса и гиперболы)

 — эксцентриситет (  для эллипса,   для параболы,   — для гиперболы)

 — истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела

Орбитальная скорость также может вычисляться по следующим формулам:

в общем виде: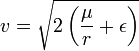 

для эллиптической орбиты: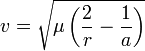 

параболическая траектория: 

гиперболическая траектория: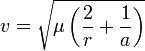 

где:

 — гравитационный параметр

 — расстояние между вращающимся телом и центральным телом

 —удельная орбитальная энергия

 — длина большой полуоси

При этом

эллиптические скорости 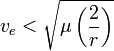  соответствуют движению по эллиптическим траекториям

частным случаем эллиптической скорости является круговая, или первая космическаяскорость

параболическая скорость 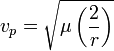  соответствует движению по параболической траектории и называется так же второй космической скоростью

гиперболические скорости 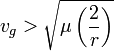  соответствуют движению по гиперболическим траекториям

Условие элллиптичности , параболичности и гиперболичности движения планеты

для эллиптической орбиты: 

параболическая траектория: 

гиперболическая траектория: 

22.

Элементы орбит планет(спутника).

Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:

большая полуось ( ),

эксцентриситет ( ),

наклонение ( ),

аргумент перицентра ( ),

долгота восходящего узла ( ),

средняя аномалия ( ).

Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию плоскости орбиты по отношению к базовой системе координат, шестой — положение тела на орбите.

Понятие о космических скоростях.

Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:

v1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности);

v2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжениенебесного тела и уйти на бесконечность;

v3 — покинуть звёздную систему, преодолев притяжение звезды;

v4 — покинуть галактику.

Вторая космическая скорость в   раза больше первой.

Обобщение и уточнение закон Кеплера и Ньютоном

Орбитальная скорость тела (обычно планеты,естественного или искусственного спутника, кратной звезды) — это скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.

Определение 

В полярных координатах выражение для орбитальной скорости ( ) при кеплеровском движении поконическому сечению (эллипсу, параболе или гиперболе) имеет следующий вид[1]:

где:

 — гравитационный параметр, равный G(M+m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела

 — фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение   — для эллипса и гиперболы)

 — эксцентриситет (  для эллипса,   для параболы,   — для гиперболы)

 — истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела

Орбитальная скорость также может вычисляться по следующим формулам:

в общем виде: 

для эллиптической орбиты: 

параболическая траектория: 

гиперболическая траектория: 

где:

 — гравитационный параметр

 — расстояние между вращающимся телом и центральным телом

 —удельная орбитальная энергия

 — длина большой полуоси

эллиптические скорости   соответствуют движению по эллиптическим траекториям

частным случаем эллиптической скорости является круговая, или первая космическаяскорость

параболическая скорость   соответствует движению по параболической траектории и называется так же второй космической скоростью

гиперболические скорости   соответствуют движению по гиперболическим траекториям

23.

Возмущения

Возмущения небесных тел, отклонения реальных траекторий небесных тел от траекторий, по которым они двигались бы в случае взаимодействия с одним единственным телом (см. Двух тел задача). Траектории движения в задаче двух тел представляют собой так называемые конические сечения — эллипс, параболу, гиперболу. Движение по коническому сечению можно рассматривать как первое приближение при условии, что одна из притягивающих масс значительно превосходит по своей величине все остальные. Так, например, в Солнечной системе движение планет вокруг Солнца можно рассматривать, в первом приближении, как движение по эллиптическим орбитам. Взаимные возмущения планет в этом случае малы и могут быть вычислены путём разложений в ряды по степеням малых параметров (аналитические методы) или численным интегрированием уравнений движения (численные методы). За малые параметры принимают обычно массы планет, выраженные в единицах массы Солнца, а также эксцентриситеты и наклоны их орбит. Члены ряда называются возмущениями или неравенствами в движении небесных тел и имеют вид:Atm, где m = 1, 2,..., и A sin (at + b). Члены первого вида называются вековыми возмущениями, второго вида — периодическими. КоэффициентыА содержат множителем массы планет в различных положительных степенях и потому являются малыми величинами. Возмущения, содержащие массы планет в первой степени, называются возмущениями первого порядка, во второй степени второго порядка и т.д. При построении теории движения больших планет приходится учитывать возмущения второго порядка и некоторые возмущения третьего порядка. Среди периодических возмущений особого внимания требуют те, у которых коэффициент a в аргументе тригонометрической функции очень мал. Так как период возмущения равен 360°/a, то при малом a период соответствующего возмущения очень велик по сравнению с периодом обращения самой планеты вокруг Солнца; такие возмущения называются долгопериодическими.

Причиной возмущений в движении небесных тел, в том числе и искусственных (см. Искусственные спутники Земли), может быть притяжение других небесных тел, отклонения фигур этих тел от сферической формы, сопротивление среды, в которой происходит движение, изменение массы тела с течением времени, световое давление и т.п. В случае двойных звёзд возмущения вызываются притяжением других близких звёзд, а также общим гравитационным полем галактики. Определение В. н. т. представляет весьма громоздкую задачу в вычислительном отношении. Так, например, в теории движения Луны, предложенной Э. Брауном, солнечные возмущения в формуле, по которой определяется долгота Луны, содержат 312 тригонометрических членов. Для вычисления возмущений по готовым разложениям в ряды, а также и для получения самих тригонометрических рядов по заданным элементам орбитнебесных тел с успехом применяются быстродействующие электронные вычислительные машины. При численном интегрировании уравнений движения можно непосредственно получить возмущённые координаты небесных тел, и тогда вопрос о вычислении возмущений отпадает (метод Коуэлла). Теория возмущённого движения небесных тел составляет основное содержание небесной механики.

Открытие Нептуна

Открытие Нептуна — обнаружение восьмой планетыСолнечной системы, одно из важнейшихастрономических открытий XIX века, сделанное благодаря предварительным вычислениям (согласно фразе Д. Араго, ставшей крылатой — «планета, открытая на кончике пера»). Нептун был открыт вБерлинской обсерватории 24 сентября 1846 года[1]И. Галле и его помощником д’Арре на основании расчётов У. Леверье. Независимо от Леверье аналогичные расчёты для поисков заурановой планеты произвёл Д. К. Адамс. Обнаружению восьмой планеты предшествовала длительная история исследований и поисков.

Понятие о задаче трех и более тел

Комплекс задач о взаимодействии многих тел достаточно обширный, и является одним из базовых, далеко не полностью разрешённых, разделов механики. В рамках ньютоновской концепции проблема ветвится на:

комплекс задач столкновения двух и более материальных тел, когда влияние тел друг на друга ограничено временем их непосредственного соприкосновения;

связные колебания материальных тел при ограниченном влиянии тел друг на друга соседними телами;

комплекс задач о взаимном движении тел под влиянием гравитационных, электрических полей всех тел друг на друга.

Иными словами, комплекс задач разделяется по условию взаимодействия тел между собой, когда теми или иными нюансами взаимодействий можно пренебречь. В первом случае пренебрегают взаимодействием вне прямого контакта между телами. Во втором случае пренебрегают взаимодействиями с несоседними элементами системы. В третьем случае, как правило, не рассматривают задачи непосредственного контакта между телами. Указанные ограничения обусловлены сложностью общего решения задачи, которое по идее должно в себя включать все три комплекса задач.

Законы кеплера в формулеровки ньютона

 В начале 17 в. И. Кеплером были установлены эмпирическим путём основные закономерности движения планет (Кеплера законы). Исходя из них, современники Ньютона (французский астроном И. Бульо, итальянский физик Дж. Борелли, английский физик Р. Гук) высказывали соображения, что движение планет может быть объяснено действием силы, которая притягивает каждую планету к Солнцу и которая убывает пропорционально квадрату расстояния от Солнца. Однако только Ньютон в «Математических началах натуральной философии» (1687) впервые это строго доказал, опираясь на свои первые два закона механики (см.Ньютона законы механики) и на созданные им новые математические методы, составившие основу дифференциального и интегрального исчисления. Ньютон доказал, что движение каждой планеты должно подчиняться первым двум законам Кеплера именно в том случае, если они движутся под действием силы тяготения Солнца в соответствии с формулой (1). Далее Ньютон показал, что движение Луны может быть приближённо объяснено с помощью аналогичного силового поля Земли и что сила тяжести на Земле есть результат воздействия этого же силового поля на материальные тела вблизи поверхности Земли. На основании 3-го закона механики Ньютон заключил, что притяжение есть взаимное свойство, и пришёл к формулировке своего закона тяготения для любых материальных частиц. Выведенный по эмпирическим данным, на основании результатов наблюдений, с неизбежностью приближённых, Н. з. т. представлял собой вначале рабочую гипотезу. В дальнейшем потребовалась колоссальная работа в течение более чем двухсот лет для строгого обоснования этого закона.

Определение масс Земли,Луны,Солнца

Массу небесного тела можно определить: а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ); б) по третьему (уточненному) закону Кеплера; в) из анализа наблюдаемых возмущений, производимых небесным. телом в движениях других небесных тел.

т — масса Земли, a R — ее радиус. Отсюда масса Земли

Ускорение силы тяжести g (точнее, ускорение составляющей силы тяжести, обусловленной только силой притяжения), так же как и радиус Земли R , определяется из непосредственных измерений на поверхности Земли (см. § 46 и 62). Постоянная тяготения f достаточно точно определена из опытов Кэвендиша и Йолли, хорошо известных в физике.

С принятыми в настоящее время значениями величин g, R и f по формуле (2.25) получается масса Земли

Зная массу Земли и ее объем, легко найти среднюю плотность Земли. Она равна 5,52 г/см3

Третий, уточненный закон Кеплера позволяет определить соотношение между массой Солнца и массой планеты, если у последней имеется хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг нее.

Действительно, движение спутника вокруг планеты подчиняется тем же законам, что и движение планеты вокруг Солнца и, следовательно, уравнение (2.24) может быть записано в этом случае так:

где — М, т и mc — массы Солнца, планеты и ее спутника, Т и tc — периоды обращений планеты вокруг Солнца и спутника вокруг планеты, a и ас — расстояния планеты от Солнца и спутника от планеты соответственно.

Разделив числитель и знаменатель левой части дроби этого уравнения па т и решив его относительно масс, получим

(2.26)

Отношение   для всех планет очень велико; отношение же    наоборот, мало (кроме Земли и ее спутника Луны) и им можно пренебречь. Тогда в уравнении (2.26) останется только одно неизвестное отношение  , которое легко из него определяется. Например, для Юпитера определенное таким способом обратное отношение   равно 1 : 1050.

Так как масса Луны, единственного спутника Земли, сравнительно с земной массой достаточно большая, то отношением   в уравнении (2.26) пренебрегать нельзя. Поэтому для сравнения массы Солнца с массой Земли необходимо предварительно определить массу Луны. Точное определение массы Луны является довольно трудной задачей, и решается она путем анализа тех возмущений в движении Земли, которые вызываются Луной.

Под влиянием лунного притяжения Земля должна описывать в течение месяца эллипс вокруг общего центра масс системы Земля — Луна.

По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые “лунным неравенством”. Наличие “лунного неравенства” в видимом движении Солнца указывает на то, что центр Земли действительно описывает небольшой эллипс в течение месяца вокруг общего центра масс “Земля — Луна”, расположенного внутри Земли, на расстоянии 4650 км от центра Земли. Это позволило определить отношение массы Луны к массе Земли, которое оказалось равным  . Положение центра масс системы “Земля — Луна” было найдено также из наблюдений малой планеты Эрос в 1930—1931 гг. Эти наблюдения дали для отношения масс Луны и Земли величину    . Наконец, по возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось равным  . Последнее значение наиболее точное, и в 1964 г. Международный астрономический союз принял его как окончательное в числе других астрономических постоянных. Это значение подтверждено в 1966 г. вычислением массы Луны по параметрам обращения ее искусственных спутников.

С известным отношением масс Луны и Земли из уравнения (2.26) получается, что масса Солнца M в 333 000 раз больше массы Земли, т.е.

M   2  1033 г.

Зная массу Солнца и отношение этой массы к массе любой другой планеты, имеющей спутника, легко определить массу этой планеты.

Массы планет, не имеющих спутников (Меркурий, Венера, Плутон), определяются из анализа тех возмущений, которые они производят в движении других планет или комет. Так, например, массы Венеры и Меркурия определены по, тем возмущениям, которые они вызывают в движении Земли, Марса, некоторых малых планет (астероидов) и кометы Энке — Баклунда, а также по возмущениям, производимым ими друг на друга.

 Определение массы планеты

Первый член разложения гравитационного потенциала имеет вид  . Если бы другие члены разложения не оказывали никакого действия на движение спутников, или, хотя бы возмущения от них были за пределами точности наблюдения, движение спутника подчинялось бы закону Кеплера.

Пусть   -- масса планеты, которую нужно определить,   -- масса спутника. Под действием сил притяжения, подчиняющихся закону обратных квадратов, оба небесных тела движутся по эллиптическим орбитам, в фокусе каждой из них расположен центр масс системы (барицентр). В частном случае -- это могут быть и круговые орбиты. Для упрощения вопроса именно этот случай мы и будем рассматривать. Пусть   -- расстояние спутника от планеты,   -- расстояние спутника от барицентра, тогда  . Двигаясь по круговой орбите, спутник имеет ускорение, равное  , где  , а   -- период обращения спутника. Отсюда   При   выражение в скобках можно не отличать от единицы и формулу для определения массы планеты переписать в следующем виде

(3.26)

Полученная формула есть не что иное, как третий закон Кеплера: квадраты периодов обращения планет, относятся так же, как кубы их расстояний до центрального тела (Солнца).

Правда, формулу (3.26) мы получили для частного случая кругового движения, хотя в небесной механике доказано, что она справедлива и для эллиптического движения. В этом случае под   нужно понимать большую полуось эллиптической орбиты.

Формула (3.26) дает возможность определить массу планеты только в том случае, когда гравитационная постоянная нам известна. Ее определяют с помощью физического эксперимента. К сожалению, точность этих экспериментов пока еще не достаточно высока, хотя со времени Кавендиша -- английского ученого, который одним из первых определил гравитационную постоянную, точность ее определения выросла на два порядка за 150 лет. Сейчас принято  СИ. Произведения гравитационной постоянной на массу определяются значительно точнее. Например, для Земли эта величина равна  , то есть относительная погрешность равна  , тогда как относительная погрешность гравитационной постоянной составляет приблизительно  . В качестве фундаментальных постоянных часто рассматривают именно произведения масс на гравитационную постоянную, которые называют планетоцентрическими гравитационными постоянными ( геоцентрическая, селеноцентрическая, ареоцентрическая и т.д.)

25.

Лунно-солнечная прецессия и следствие из нее.

Предварение равноденствий (лат. praecessio aequinoctiorum) — историческое название для постепенного смещения точек весеннего и осеннегоравноденствий (то есть точек пересечения небесного экватора с эклиптикой) навстречу видимому годичному движению Солнца. Другими словами, каждый год весеннее равноденствие наступает немного раньше, чем в предыдущем году.

равноденствий — прецессия, периодическое изменение направления земной оси под влиянием притяженияЛуны, а также (в меньшей степени) Солнца. Как выяснил Ньютон в своих «Началах», сплюснутость Земли у полюсов приводит к тому, что притяжение внешних тел поворачивает земную ось, которая описывает конус с периодом (по современным данным) примерно 25 776 лет. При этом наклон земной оси к эклиптике сохраняется неизменным. Поворот земной оси смещает и связанные с Землёй экваториальные системы небесных координат, примерно на 20,1" в год.

Существуют и другие причины смещения земной оси — нутация, апериодическое «блуждание полюсов» и т. п., однако их вклад в результат по сравнению с прецессией невелик.

Аналогичные явления происходят и на других планетах. Например, ось Юпитера под влиянием его многочисленных спутников и Солнца смещается примерно на полградуса в течение юпитерианского года.

Нутация

Нута́ция (от лат. nūtāre — колебаться) — слабое нерегулярное движениевращающегося твёрдого тела, совершающего прецессию. Напоминает «подрагивание» оси вращения и заключается в слабом изменении так называемого угла нутации между осями собственного и прецессионного вращения тела.

Чистая нутация — это такое движение оси вращения, при котором первый угол Эйлера остаётся постоянным. В случае асимметрического волчка описывается траекториями мгновенной угловой скорости волчка (полодия и герполодия[1][2]).

В астрономии нутацией называют небольшие колебания земной оси, накладывающиеся на прецессионное движение. Это явление открыто в1728 году Джеймсом Бредли. Вследствие нутации изменяются наклон эклиптики кэкватору, а также экваториальные координаты небесных светил.

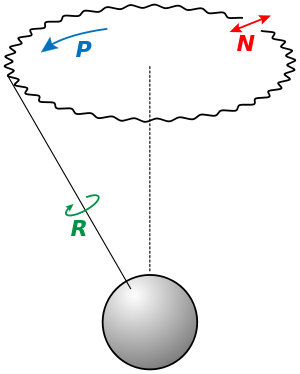
Лунно-солнечные приливы и отливы.

Прили́в и отли́в — периодические вертикальные колебания уровня океана илиморя, являющиеся результатом изменения положений Луны иСолнца относительно Земли вкупе с эффектами вращения Земли и особенностями данного рельефа и проявляющееся в периодическом горизонтальном смещении водных масс. Приливы и отливы вызывают изменения в высоте уровня моря, а также периодические течения, известные как прили́вные течения, делающие предсказание приливов важным для прибрежной навигации.

Интенсивность этих явлений зависит от многих факторов, однако наиболее важным из них является степень связи водоёмов с мировым океаном. Чем более замкнут водоём, тем меньше степень проявления приливо-отливных явлений.

Приливная сила и её практическое использование.

Прили́вные си́лы — силы, возникающие в телах, свободно движущихся в неоднородном силовом поле. Самым известным примером действия приливных сил являются приливы и отливы наЗемле, откуда и произошло их название.

В самом общем случае приливные силы представляют собой силы, вызывающие эффекты, проявляющиеся при воздействии неоднородного силового поля на протяжённый объект, независимо от того, какое движение он совершает и чем это поле вызвано. Силовое поле может иметь либо гравитационную, либо электромагнитную природу (в том случае, если тело обладает электрическим зарядом, неподвижным или движущимся относительно источников поля).

Так, в гравитационном поле нарастающей интенсивности (то есть с постоянным градиентом модуля силы тяжести) спиральная пружина будет свободно падать по прямой с нарастающим ускорением, растянувшись в направлении падения на постоянную величину настолько, чтобы её силы упругости уравновесили бы градиент интенсивности гравитационного поля.

30

Со́лнце (астр. ☉) — единственная звезда Солнечной системы, дневное светило. Вокруг Солнца обращаются другие объекты этой системы: планеты и их спутники, карликовые планеты и их спутники, астероиды, метеориты, кометы и космическая пыль. Это  звезда с диаметром 1400000 км, то есть в 109 раз большим, чем диаметр Земли. Общеизвестно, что солнечное тепло и свет — источники нашей жизни.

Внутреннее строение Солнца

Строение Солнца. В центре Солнца находится солнечное ядро. Фотосфера — это видимая поверхность Солнца, которая и является основным источником излучения. Солнце окружает солнечная корона, которая имеет очень высокую температуру, однако она крайне разрежена, поэтому видима невооружённым глазом только во время полного солнечного затмения.

Солнечное ядро

Зона лучистого переноса

Конвективная зона Солнца

Фотосфера

Хромосфера

Корона

Центральная часть Солнца с радиусом примерно 150—175 тыс. км (то есть 20—25 % от радиуса Солнца), в которой идут термоядерные реакции, называется солнечным ядром. Плотность вещества в ядре составляет примерно 150 000 кг/м³ (в 150 раз выше плотности воды и в ~6,6 раз выше плотности самого плотного металла на Земле — осмия), а температура в центре ядра — более 14 млн К.

В ядре осуществляется протон-протонная термоядерная реакция, в результате которой из четырёх протонов образуется гелий-4. При этом каждую секунду в излучение превращаются 4,26 млн тонн вещества, однако эта величина ничтожна по сравнению с массой Солнца — 2·1027 тонн. Мощность, выделяемая различными зонами ядра, зависит от их расстояния до центра Солнца.

Фотосфера (слой, излучающий свет) образует видимую поверхность Солнца. Её толщина соответствует оптической толщине приблизительно в 2/3 единиц. В абсолютных величинах фотосфера достигает толщины, по разным оценкам, от 100 до 400 км.

Хромосфера  — внешняя оболочка Солнца толщиной около 2000 км, окружающая фотосферу. Верхняя граница хромосферы не имеет выраженной гладкой поверхности, из неё постоянно происходят горячие выбросы, называемые спикулами. Число спикул, наблюдаемых одновременно, составляет в среднем 60—70 тыс. Из-за этого в конце XIX века итальянский астроном Секки, наблюдая хромосферу в телескоп, сравнил её с горящими прериями. Температура хромосферы увеличивается с высотой от 4000 до 20 000 К (область температур больше 10 000 К относительно невелика).

Магнитные поля

Так как солнечная плазма имеет достаточно высокую электропроводность, в ней могут возникать электрические токи и, как следствие, магнитные поля. Непосредственно наблюдаемые в солнечной фотосфере магнитные поля принято разделять на два типа, в соответствии с их масштабом.

Крупномасштабное (общее илиглобальное) магнитное поле с характерными размерами, сравнимыми с размерами Солнца, имеет среднюю напряжённость на уровне фотосферы порядка нескольких гаусс. В минимуме цикла солнечной активности оно имеет приблизительно дипольную структуру, при этом напряжённость поля на полюсах Солнца максимальна. 

Средне- и мелкомасштабные (локальные) поля Солнца отличаются значительно бо́льшими напряжённостями полей и меньшей регулярностью. Самые мощные магнитные поля (до нескольких тысяч гаусс) наблюдаются в группах солнечных пятен в максимуме солнечного цикла.

31

Физические процессы внутри Солнца.

Выделение термоядерной энергии происходит в центральной области Солнца (ядре), радиус которой около четверти радиуса всего Солнца. Дальше от центра выделение энергии за счет ядерных реакций быстро ослабевает и на расстоянии около 0,3 радиуса становится несущественным. На протяжении расстояний, примерно, от 0,3 до 0,7 радиуса Солнца находится лучистая зона, в которой энергия переносится лишь путем последовательных процессов поглощения квантов и последующего их переизлучения. При этом поглощаются чаще всего более энергичные кванты рентгеновских и ультрафиолетовых лучей, а вместо них чаще излучаются менее энергичные видимые и инфракрасные лучи. В результате общая энергия, переизлучаемая сферическими слоями, площадь которых увеличивается с удалением от центра Солнца, сохраняется, а их температура постепенно уменьшается. Последняя треть радиуса приходится на конвективную зону, в которой происходит перемешивание вещества (конвекция), и перенос энергии осуществляется движением самого вещества. Конвективная зона переходит в нижние слои солнечной атмосферы – фотосферу, где температура продолжает уменьшаться вплоть до минимального для всего Солнца значения около 4200К.

Пожалуй, наиболее характерными являются так называемые эруптивные протуберанцы. Такие газовые образования в течение нескольких дней могут иметь вид спокойного облака, или длинной струи дыма, или, наконец, арки. На этой стадии внутри протуберанца никаких заметных движений нет. Но затем они переходят в фазу бурного развития, когда возникают вихревые вращения всего протуберанца или поднимается одно из колен арки. Эти перестройки осуществляются быстро - в течение нескольких минут. Протуберанец начинает растягиваться, подниматься. Происходит как бы замедленный взрыв. Яркость его увеличивается, а потом сразу же ослабевает. 

Протуберанцы, приуроченные к областям солнечных пятен. Для таких протуберанцев свойственно движение газовых струй и узлов по определенным искривленным траекториям, напоминающим силовые линии некоторых магнитных полей.

Комплекс явлений, вызванных генерацией сильных магнитных полей на Солнце, называют солнечной активностью. Эти поля проявляются в фотосфере как солнечные пятна и вызывают такие явления, как солнечные вспышки, генерацию потоков ускоренных частиц, изменения в уровнях электромагнитного излучения Солнца в различных диапазонах, корональные выбросы массы, возмущения солнечного ветра, вариации потоков галактических космических лучей (Форбуш-эффект) и т. д.

С солнечной активностью связаны также вариации геомагнитной активности (в том числе и магнитные бури), которые являются следствием достигающих Земли возмущений межпланетной среды, вызванных, в свою очередь, активными явлениями на Солнце.

Одним из наиболее распространённых показателей уровня солнечной активности является число Вольфа, связанное с количеством солнечных пятен на видимой полусфере Солнца. Общий уровень солнечной активности меняется с характерным периодом, примерно равным 11 годам (так называемый «цикл солнечной активности» или «одиннадцатилетний цикл»). Этот период выдерживается неточно и в XX веке был ближе к 10 годам, а за последние 300 лет варьировался примерно от 7 до 17 лет. Циклам солнечной активности принято приписывать последовательные номера, начиная от условно выбранного первого цикла, максимум которого был в 1761 году.

32

Астрофи́зика (от др.-греч. ἀστήρ — «звезда, светило» и φυσικά — «природа») — наука на стыке астрономии и физики, изучающая физические процессы в астрономических объектах, таких, как звёзды, галактики и т. д. Физические свойства материи на самых больших масштабах и возникновение Вселенной изучает космология.

Главные экспериментальные методы астрофизики: спектральный анализ, фотография и фотометрия вместе с обыкновенными астрономическими наблюдениями. 

Законы Вина — законы излучения абсолютно чёрного тела, выведенные Вильгельмом Вином в 1893—1896 годах 

Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.

Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.

Первый закон излучения Вина[править]

В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:

где uν — плотность энергии излучения,

ν — частота излучения,

T — температура излучающего тела,

f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.

Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.

Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.

Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума.

Второй закон излучения Вина[править]

В 1896 году Вин на основе дополнительных предположений вывел второй закон:

где C1, C2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.

Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C1 и C2. С учётом этого, второй закон Вина можно записать в виде:

где h — постоянная Планка,

k — постоянная Больцмана,

c — скорость света в вакууме.

Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры.

Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.

Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится, и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты звуковых волн.

Я́ркость источника света — это световой поток, посылаемый в данном направлении, деленный на малый (элементарный) телесный угол вблизи этого направления и на проекцию площади источника на плоскость, перпендикулярную оси наблюдения. Иначе говоря - это отношение силы света, излучаемого поверхностью, к площади её проекции на плоскость, перпендикулярную оси наблюдения.

Закон Ламберта — физический закон, согласно которому яркость   рассеивающей свет (диффузной) поверхности одинакова во всех направлениях.

Альбе́до (лат. albus — белый) — характеристика отражательной (рассеивающей) способности поверхности.

Значение альбедо для данной длины волны или диапазона длин волн зависит от спектральных характеристик отражающей поверхности, поэтому альбедо отличается для разных спектральных диапазонов (оптическое, ультрафиолетовое, инфракрасное альбедо) или длин волн (монохроматические альбедо).

Ламбертово (истинное, плоское) альбедо 

Истинное или плоское альбедо — коэффициент диффузного отражения, то есть отношение светового потока, рассеянного плоским элементом поверхности во всех направлениях, к потоку, падающему на этот элемент. В случае освещения и наблюдения, нормальных к поверхности, истинное альбедо называют нормальным.

Нормальное альбедо чистого снега составляет ~0,9, древесного угля ~0,04.

Геометрическое альбедо 

В планетной фотометрии геометрическое (плоское) альбедо   определяется отношением освещённости у Земли, создаваемой планетой в полной фазе  , к освещённости  , которую создал бы плоский абсолютно белый экран того же размера, что и планета, расположенный на её месте перпендикулярно лучу зрения и солнечным лучам[1][2].

Геометрическое оптическое альбедо Луны — 0,12, Земли — 0,367.

Бондовское (сферическое) альбедо 

Альбедо Бонда     определяется как отношение светового потока, рассеянного сферическим телом во всех направлениях, к потоку, падающему на тело. Альбедо Бонда связано с геометрическим альбедо следующим отношением:  , где   — геометрическое альбедо, а   — фазовый интеграл, учитывающий только ту часть освещённой поверхности, которая видна наблюдателю[3]. Бондовское альбедо Земли — около 0,29, Луны — 0,067[4].

Звёздная величина́ (блеск) — безразмерная числовая характеристика яркости объекта. Обычно понятие применяется к небесным светилам. Звёздная величина характеризует поток энергии от рассматриваемого светила (энергию всех фотонов в секунду) на единицу площади. Таким образом, видимая звёздная величина зависит и от физических характеристик самого объекта (то есть светимости), и от расстояния до него. Чем меньше значение звёздной величины, тем ярче данный объект. Понятие звёздной величины используется при измерении потока энергии в видимом, инфракрасном и ультрафиолетовом диапазоне.

33

Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя.

БЛЕСК небесного светила, освещенность, создаваемая светилом в месте наблюдения на перпендикулярной к лучам плоскости

Яркость – это фотометрическая величина, характеризующая излучательную способность протяжённых тел в данном направлении. 

В астрономии яркость часто измеряется видимой звёздной величиной поверхности площадью в одну квадратную секунду дуги. Ранее в Международной системе единиц (СИ) за единицу яркости принимали 1 нит (1 нт=10кд/м2).

Астрономи́ческий катало́г или каталог звёздного неба — список астрономических объектов (звёзд, туманностей, галактик и др.), сгруппированных по типу, морфологии, происхождению, средству выявления или методу открытия.

В астрономии большинство объектов обозначаются номером, присвоенным им в каталогах звёздного неба. Существует большое количество каталогов, созданных для разных целей. Многие из них доступны в электронном виде и могут быть свободно загружены с сайта Астрофизической информационной системы NASA или из других источников.

34

Диаграмма Герцшпрунга — Рассела (варианты транслитерации: диаграмма Герцшпрунга — Рессела, Расселла, или просто диаграмма Г-Р или диаграмма цвет — звёздная величина) показывает зависимость между абсолютной звёздной величиной, светимостью, спектральным классом и температурой поверхности звезды. Неожиданным является тот факт, что звёзды на этой диаграмме располагаются не случайно, а образуют хорошо различимые участки.

Была предложена примерно в 1910 году независимо Эйнаром Герцшпрунгом (Дания) и Генри Расселом (США). Диаграмма используется для классификации звёзд и соответствует современным представлениям о звёздной эволюции.

Диаграмма даёт возможность (хотя и не очень точно) найти абсолютную величину по спектральному классу. Особенно для спектральных классов O—F. Для поздних классов это осложняется необходимостью сделать выбор между гигантом и карликом. Однако определённые различия в интенсивности некоторых линий позволяют уверенно сделать этот выбор.

Вместо спектрального класса в качестве координаты на графике могут использоваться показатель цвета или эффективная температура звезды, а вместо абс. звёздной величины -светимость звезды. Спектральный класс и показатель цвета определяются в основном темп-рой звезды. 

Назв. Г.- P. д. связано с именами Э. Герцшпрунга (E. Hertzsprung), к-рый в 1905-07 построил первую диаграмму видимая звёздная величина - показатель цвета для звёзд в скоплениях Плеяды и Гиады, и Г. Ресселла (H. Russell), к-рый в 1914 опубликовал первую диаграмму спектральный класс - абс. звёздная величина.

Диаграмма показатель цвета - абсолютная звездная величина звёзд нескольких рассеянных звездных скоплений и одного шарового скопления (МЗ). Точка, где звёзды скопления сворачивают с главной последовательности, указывает возраст звёзд скопления.

35

Визуальная фотометрия.

ФОТОМЕТРИЯ, раздел прикладной физики, занимающийся измерениями света. С точки зрения фотометрии, свет – это излучение, способное вызывать ощущение яркости при воздействии на человеческий глаз.

Поток световой энергии измеряется в люменах. Определить световой поток в 1 лм невозможно, не обращаясь к светящимся телам, и основной мерой света долгое время была «свеча», которая считалась единицей силы света. 

Виды фотометрических измерений.

Основные виды фотометрических измерений таковы: 1) сравнение силы света источников; 2) измерение полного потока от источника света; 3) измерение освещенности в заданной плоскости; 4) измерение яркости в заданном направлении; 5) измерение доли света, пропускаемой частично прозрачными объектами; 6) измерение доли света, отражаемой объектами.

Фото́метр — прибор для измерения каких-либо из фотометрических величин, чаще других — одной или нескольких световых величин.

При использовании фотометра осуществляют определённое пространственное ограничение потока излучения и регистрацию его приёмником излучения с заданной спектральной чувствительностью. Освещённость измеряютлюксметрами, яркость — яркомерами, световой поток и световую энергию — с помощью фотометра интегрирующего. 

Фотометры находят широкое применение в лабораторной практике. Например, с помощью фотометров можно определять спектр образцов, что позволяет установить их химический состав. Особый класс этих приборов – пламенные фотометры – предназначен для выявления в образцах наличия щелочных металлов (литий, натрий,калий). Для этого образец сжигается при высокой температуре, а анализ спектра пламени с помощью фотометра позволяет выявить наличие щелочных металлов в образце.

 Блеск ярких звезд можно оценивать невооруженным глазом, более слабых — в бинокль, а еще более слабых — в те­лескоп. Увлекательность этих наблюдений очевидна: при их выполнении наблюдатель подобно своим антич­ным предшественникам общается с небом, видит про­исходящие на нем изменения.

Фотоэлектрические наблюдения, кроме задач космической геодезии, позволяют выполнять и другие интересные исследования. Во-первых, фотоэлектрический метод дает возможность решать все задачи, доступные визуальному методу, но с повышенной точностью. Это такие вопросы, как определение поправок к орбитальной долготе и широте Луны, поправки эфемеридного времени. Во-вторых, фотоэлектрические наблюдения покрытий - это ценный материал для решения некоторых астрофизических задач. Если регистрировать изменения блеска звезды в момент ее покрытия краем Луны, то по характеру этих изменений удается получить диаметр покрываемой звезды. Другая важная задача - это обнаружение двойных и кратных систем звезд и измерение угловых расстояний между их компонентами. Методом лунных покрытий при использовании фотоэлектрической регистрация можно "наблюдать" двойные системы в 100 раз более тесные, чем при наблюдении любыми другими методами. Регистрация изменения блеска звезды за время покрытия составляет основную задачу фотоэлектрического метода наблюдений.

36

Телеско́п (от др.-греч. τῆλε[tele] — далеко + σκοπέω[skopein] — смотрю) — прибор, предназначенный для наблюдения небесных тел.

Оптические телескопические системы используют в астрономии (для наблюдения за небесными светилами), в оптике для различных вспомогательных целей: например, для изменения расходимости лазерного излучения. Также, телескоп может использоваться в качестве зрительной трубы, для решения задач наблюдения за удалёнными объектами.

Телескоп представляет собой трубу (сплошную, каркасную или ферму), установленную на монтировке, снабжённой осями для наведения на объект наблюдения и слежения за ним. Визуальный телескоп имеет объектив и окуляр. Задняя фокальная плоскость объектива совмещена с передней фокальной плоскостью окуляра[6]. В фокальную плоскость объектива вместо окуляра может помещаться фотоплёнка или матричный приёмник излучения. В таком случае объектив телескопа, с точки зрения оптики, является фотообъективом[7]. Телескоп фокусируется при помощи фокусера (фокусировочного устройства).

По своей оптической схеме большинство телескопов делятся на:

Линзовые (рефракторы или диоптрические) — в качестве объектива используется линза или система линз.

Зеркальные (рефлекторы или катаптрические) — в качестве объектива используется вогнутое зеркало.

Зеркально-линзовые телескопы (катадиоптрические) — в качестве объектива используется сферическое зеркало, а линза, система линз илимениск служит для компенсации аберраций.

Основная характеристика окуляра-фокусное расстояние; поделив фокусное расстояние объектива на фокусное расстояние окуляра, можно определить увеличение телескопа.

Например, если фокусное расстояние окуляра равно 25 мм, а объектива-1 м, то увеличение телескопа-40 раз. Нередко значения фокусных расстояний окуляров (и телескопов), указанные на их корпусах, слегка отличаются от реальных, поэтому увеличение телескопа лучше измерять самим.

Чтобы получить увеличение, поделите диаметр линзы объектива (или первичного зеркала телескопа) на диаметр выходного зрачка. Этот сравнительно простой метод позволяет довольно точно определить увеличение телескопа.

 Угломерные инструменты.

Для простейших угловых измерений надо прежде всего иметь транспортиры с отвесом - высотомеры

Для тех случаев, когда измеряется угловое расстояние между звёздами, расположенными как угодно, надо изготовить простой угломер.

 В морской навигации необходимым инструментом для определения положения корабля является секстант.

Необходимым элементом набора приборов для наблюдений являются часы.

37

Общая характеристика звезд.

ЗВЕЗДЫ - это горячие светящиеся небесные тела, подобные Солнцу. Звезды различаются по размеру, температуре и яркости. По многих параметрам Солнце – типичная звезда, хотя кажется гораздо ярче и больше всех остальных звезд, поскольку расположено намного ближе к Земле. Даже ближайшая звезда (Проксима Кентавра) в 272 000 раз дальше от Земли, чем Солнце, поэтому звезды кажутся нам светлыми точками на небе. Хотя звезды рассыпаны по всему небосводу, мы видим их только ночью, а днем на фоне яркого рассеянного в воздухе солнечного света они не видны. 

Светимость звезд.  Полную мощность излучения звезды во всем диапазоне электромагнитного спектра называют истинной или болометрической «светимостью». Например, светимость Солнца 3,86ґ1026 Вт. Чем больше масса нормальной звезды, тем выше ее светимость; она возрастает примерно как куб массы. Это соотношение масса – светимость сначала было найдено из наблюдений, а позже получило теоретическое обоснование. Поток энергии, приходящий от звезды на Землю, называют «видимым блеском»; он зависит не только от истинной светимости звезды, но и от ее расстояния до Земли. Звезда низкой светимости, расположенная близко к Земле, может иметь больший блеск, чем звезда высокой светимости на большом расстоянии. Массы звезд Масса звезды — одна из важнейших ее характеристик. Массы звезд различны. Однако, в отличие от светимостей и размеров, массы звезд заключены в сравнительно узких пределах: самые массивные звезды обычно лишь в десятки раз превосходят Солнце, а наименьшие массы звезд порядка 0,06Мо. Основной метод определения масс звезд дает исследование двойных звезд; обнаружена зависимость между светимостью и массой звезды. Расстояния до звезд. Ближайшая к нам звезда – Солнце, до него ок. 150 млн. км. Ближайшая к Солнцу яркая звезда – a Кентавра, которую можно увидеть только в Южном полушарии, до нее 42 000 млрд. км. Но еще чуть ближе к нам расположен ее невидимый глазом спутник, звезда Проксима («ближайшая») Кентавра. Всего лишь вдвое дальше расположен Сириус, ярчайшая звезда нашего неба. Поскольку расстояния до звезд так велики, их неудобно измерять в километрах. Лучше использовать специальные единицы; например, в научно-популярной литературе часто используют «световой год», т.е. расстояние, которое луч света проходит со скоростью около 300 000 км/с за год; это ок. 9460 млрд. км. Расстояние до Проксимы 4,3 св. года, а до Сириуса ок. 8,7 св. года.

Средние плотности звезд Так как размеры звезд различаются значительно больше, чем их массы, то и средние плотности звезд сильно отличаются друг от друга. У гигантов и сверхгигантов плотность очень мала. Например, плотность Бетельгейзе около 10-3 кг/м3. Вместе с тем существуют чрезвычайно плотные звезды. К ним относятся небольшие по размерам белые карлики (их цвет обусловлен высокой температурой). Например, плотность белого карлика Сириус В более 4х107 кг/м3. В настоящее время известны значительно более плотные белые карлики (1010- 1011 кг/м3). Огромные плотности белых карликов объясняются особыми свойствами вещества этих звезд, которое представляет собой атомные ядра и оторванные от них электроны. Расстояния между атомными ядрами в веществе белых карликов должны быть в десятки и даже сотни раз меньше, чем в обычных твердых и жидких телах, с которыми мы встречаемся в земных условиях. Агрегатное состояние, в котором находится это вещество, нельзя назвать ни жидким, ни твердым, так как атомы белых карликов разрушены. Мало похоже это вещество на газ или плазму. И все-таки его принято считать «газом», учитывая, что расстояние между частицами даже в плотных белых карликах во много раз больше, чем сами ядра атомов или электроны.

Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:

Мощность излучения абсолютно чёрного тела прямо пропорциональна площади поверхности и четвёртой степени температуры тела:

где   - степень черноты (для всех веществ  , для абсолютно черного тела  ). При помощи закона Планка для излучения, постоянную  можно определить как

где   — постоянная Планка,   — постоянная Больцмана,   — скорость света.

Численное значение   Дж·с−1·м−2 · К−4.

Закон открыт независимо Й. Стефаном и Л. Больцманом в предположении пропорциональности плотности энергии излучения его давлению  . В 1880 г. подтверждён Лео Гретцем.

Важно отметить, что закон говорит только об общей излучаемой энергии. Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина.

Применение закона к расчёту эффективной температуры поверхности Земли даёт оценочное значение, равное 249 К или −24 °C.

МК Спектральная классификационная система (стандартная)
Класс	Цвет	Температура, K	Состав	Примеры
O	Самые горячие звезды во Вселенной
	синий	28,000 - 50,000	ионизированные атомы, в основном, гелий	Mintaka (01-3III)
B	Менее горячие звезды
	голубой	10,000 - 28,000	нейтральный гелий, немного водорода	Alpha Eridani (B3V-IV)
A	светло-голубой	7,500 - 10,000	водород, некоторое количество ионизированных металлов	Sirius A (A0-IV)
F	белый	6,000 - 7,500	водород, ионизированные металлы, кальций и железо	Procyon A (F5V-IV)
G	Звезды со спектром, подобным солнечному
	желтый	5,000 - 6,000	ионизированный кальция, нейтральные и ионизированные металлы	Sol (G2V)
K	Звёзды более холодные, чем Солнце
	оранжевый	3,500 - 5,000	нейтральные металлы	Alpha Centauri B (K0-3V)
M	Самые холодные звезды
	красный	2,500 - 3,500	стабильные молекулы, оксид титана, нейтральный кальций	Wolf 359 (V5-8V)

Кроме того, звезды классифицируются по интенсивности излучения согласно схеме Yerkes, основанной на свечении и температуре, К:

Ia	самые яркие супергиганты
Ib	яркие супергиганты
II	яркие гиганты
III	нормальные гиганты
IV	суб-гиганты
V	карлики

Расстояние до звезд и способы его определения. Метод параллакса.

Для сравнительно близких звезд, удаленных на расстояние, не превышающие нескольких десятков парсек, расстояние определяется по параллаксу способом, известным уже двести лет. При этом измеряют ничтожно малые угловые смещения звезд при их наблюдении с разных точек земной орбиты, то есть в разное время года. Параллаксы даже самых близких звезд меньше 1". С понятием параллакса связано название одной из основных единиц в астрономии – парсек. Парсек – это расстояние до воображаемой звезды, годичный параллакс которой равен 1":   где R – расстояние в парсеках, p – годичный параллакс в секундах. 1 парсек = 3,26 светового года = 206 265 астрономических единиц = 3,083∙1016м.

Определение расстояний до ближайших звезд.

Вследствие годичного движения Земли по орбите близкие звезды немного перемещаются относительно далеких "неподвижных" звезд. За год такая звезда описывает на небесной сфере малый эллипс, размеры к-рого тем меньше, чем дальше звезда. В угловой мере большая полуось этого эллипса приблизительно равна величине макс. угла, под каким со звезды видна 1 а.е. (большая полуось земной орбиты), перпендикулярная направлению на звезду. Этот угол ( ), называемый годичным или тригонометрич. параллаксом звезды, служит для измерения расстояния до нее на основе тригонометрич. соотношений между сторонами и углами треугольника ЗСА, в к-том известен угол   и базис - большая полуось земной орбиты

38

Достоверно определить массу звезды можно, только если она является компонентом двойной звезды. В этом случае массу можно вычислить, используя обобщённый третий закон Кеплера. Но даже при этом оценка погрешности составляет от 20 % до 60 % и в значительной степени зависит от погрешности определения расстояния до звезды. Во всех прочих случаях приходится определять массу косвенно, например, из зависимости масса — светимость

Непосредственные измерения радиусов звезд, за некоторыми исключениями, практически невозможны, так как все звезды настолько далеки от нас, что их угловые размеры меньше предела разрешения крупнейших телескопов. Угловые диаметры двух-трех десятков ближайших звезд определены с помощью специальных звездных интерферометров. Принцип работы этих приборов основан на интерференции света звезды, отраженного парой широко расставленных зеркал. В отдельных случаях для определения углового диаметра звезды удается использовать вид интерференционной картины, возникающей во время покрытия звезд Луной. Линейные радиусы можно определить у затменно-переменных звезд по продолжительности затмения.

Формула для определения размера звезды по светимости и температуре

С = 4πR²(σT^4)  σ - постоянная Стефана-Больцмана  Светимость в Ваттах, радиус в метрах, температура в Кельвинах

Двойная звезда, или двойная система — система из двух гравитационно связанных звезд, обращающихся по замкнутым орбитам вокруг общего центра масс. Двойные звёзды — весьма распространённые объекты. Примерно половина всех звёзд нашей Галактики принадлежит к двойным системам

Переме́нная звезда́ — звезда, блеск которой изменяется со временем в результате происходящих в её районе физических процессов. Строго говоря, блеск любой звезды меняется со временем в той или иной степени. Например, величина выделяемой Солнцем энергии изменяется на 0,1 % в течение одиннадцатилетнего солнечного цикла, что соответствует изменению абсолютной звездной величины на одну тысячную. Переменной называется звезда, изменения блеска которой были надёжно обнаружены на достигнутом уровне наблюдательной техники. Для отнесения звезды к разряду переменных достаточно, чтобы блеск звезды хотя бы однажды претерпел изменение.

Нестационарные звёзды, звёзды, у которых наблюдается значительное нарушение равновесия внешних слоев. Оно проявляется в виде переменности блеска или спектра звезды, а также в наличии линий излучения в спектре. Строго говоря, стационарных звёзд не существует. Наше Солнце постоянно испытывает нарушения равновесия во внешних слоях в виде выброса протуберанцев. Однако характеристики Солнца как звезды — его светимость, спектр, размеры, масса — остаются неизменными в течение достаточно длительного времени, поэтому Солнце относится к стационарным звёздам. Частным, но наиболее многочисленным типом Н. з. являются физические переменные звёзды, для которых характерно изменение блеска. Наиболее общие проявления звёздной нестационарности: выброс вещества из звезды в окружающее пространство, пульсации, наличие оболочек. Выброс вещества может быть постоянным в течение определённого периода жизни звезды.

Цефеи́ды — класс пульсирующих переменных звёзд с довольно точной зависимостью период—светимость, названный в честь звезды δ Цефея. Одной из наиболее известных цефеид является Полярная звезда.

Значимость

Для астрономов цефеиды являются своего рода маяками. Ориентируясь по их переменному блеску, астрономы выясняют расстояния до удаленных объектов и определяют постоянную Хаббла. Последние исследования, основанные на данных от космического спутника Спитцера, показывают что цефеиды могут терять массу, а значит может потребоваться пересчет известных расстояний.

39

Основы современных представлений о строении и эволюции Вселенной

 Последний звёздный каталог содержит более 30 тыс. галактик ярче 15 звёздной величины, а при помощи сильного телескопа можно сфотографировать сотни миллионов галактик. Всё это вместе с нашей Галактикой образует так называемую метагалактику. По своим размерам и количеству объектов метагалактика бесконечна, она не имеет ни начала, ни конца. По современным представлениям в каждой галактике происходит вымирание звёзд и целых галактик, равно как и возникновение новых звёзд и галактик. Наука, изучающая нашу Вселенную как единое целое, называется космологией. По теории Хаббла и Фридмана наша вселенная, учитывая общую теорию Эйнштейна, такая Вселенная расширяется примерно 15 млрд лет назад ближайшие галактики были ближе к нам, чем сейчас. В каком-то месте пространства возникают новые звёздные системы и, учитывая формулу Е =mc2, поскольку можно говорить о том, что поскольку массы и энергии эквивалентны, то взаимное превращение их друг в друга представляет собой основу материального мира.

40

Звёздная система — это система, состоящая из звёзд, движущихся по замкнутой орбите, гравитационно связанных, и, возможно, имеющих планетные системы, состоящие из меньших тел (таких как планеты или астероиды). В частности, Солнечная система — это звёздная система, образованная одиночной звездой —Солнцем — и другими телами (планетами и др.), обращающимися вокруг неё.

Квазары, или квазизвездные объекты (кратко— QSO), по наблюдаемым свойствам очень похожи на ядра галактик Сейферта, но превосходят их по мощности выделения энергии в 100-1000 раз. Это — самые мощные стационарные источники оптического излучения в природе. Были открыты в 1960-х как радиоисточники с очень малыми угловыми размерами, на месте которых в оптическом диапазоне спектра видны слабые объекты, похожие на голубоватые звездочки. Однако, эти "звездочки" оказались обладающими большим красным смещением, выдающим их внегалактическую природу. Позднее выяснилось, что мощное радиоизлучение характерно только для части из них. В отличие от звезд, у квазаров оптическое излучение имеет нетепловую природу и связано с очень мощным выделением энергии (до 1041Вт) в небольшом объеме пространства. Невероятно высокая светимость квазаров позволяет уверенно наблюдать их с расстояний в миллиарды св. лет. При этом видимая яркость квазаров, как правило, заметно меняется на самых различных интервалах времени — от нескольких лет до долей суток. Как правило, излучение "материнской" галактики, внутри которой находится квазар, "тонет" в ярком свете квазара, так что ее обнаружение представляет сложную, хотя и решаемую проблему. Среди галактик, связанных с квазарами, оказались галактики различных типов. Многие из них, по-видимому, являются "пекулярными" галактиками с искаженной структурой. Квазары представляют собой кратковременную (по сравнению с возрастом галактик) стадию очень высокой активности галактических ядер, которая имеет место на определенной стадии их эволюции. Предположительно, механизм выделения энергии в квазарах (и других типах активных ядер) связан с падением вещества на сверхмассивные черные дыры, существующие в ядрах большинства массивных галактик.

Шарово́е звёздное скопле́ние (англ. globular cluster) — звёздное скопление, содержащее большое число звёзд, тесно связанное гравитацией и обращающееся вокруг галактического центра в качестве спутника. В отличие от рассеянных звёздных скоплений, которые располагаются в галактическом диске, шаровые находятся в гало; они значительно старше, содержат гораздо больше звёзд, обладают симметричной сферической формой и характеризуются увеличением концентрации звёзд к центру скопления. Пространственные концентрации звёзд в центральных областях шаровых скоплений составляют 100—1000 звёзд на кубический парсек (для сравнения — в окрестностях Солнца пространственная концентрация звёзд составляет ≈0,13 пк−3, то есть в окрестностях Солнца звёздная плотность в 700—7000 раз меньше), количество звёзд ≈104—106. Диаметры шаровых скоплений составляют 20—60 пк, массы — 104—106 солнечных.

Движущаяся группа звёзд — группа звёзд, дрейфующих в пространстве как единое целое.

В астрономии широко признано, что большинство звезд рождается в пределах молекулярных облаков, известных как звездные ясли. Звезды, сформированные в пределах такого облака, составляют рассеянное звёздное скопление, содержащие от десятков до тысяч звёзд. Эти скопления распадаются со временем. Звезды, которые вместе отделяются от ядра скопления, становятся членами звездной ассоциации. Если остаток скопления затем дрейфует по галактической орбите как нечто целое, то его называют движущейся группой.

Звёздная эволюция в астрономии — последовательность изменений, которым звезда подвергается в течение её жизни, то есть на протяжении сотен тысяч, миллионов или миллиардов лет, пока она излучает свет и тепло. В течение таких колоссальных промежутков времени изменения оказываются весьма значительными.

 Истинные размеры Галактики были установлены только в XX в. Оказалось, что она является значительно более плоским образованием, чем предполагали ранее. Диаметр галактического диска превышает 100 тыс. световых лет, а толщина - около 1000 световых лет. Из-за того что Солнечная система находится практически в плоскости Галактики, заполненной поглощающей материей, очень многие детали строения Млечного Пути скрыты от взгляда земного наблюдателя.

В состав Галактики входят: 1 - звезды (одиночные, кратные, в шаровых и рассеянных скоплениях), 2 - межзвездный газ (атомарный, молекулярный водород, другие газы и в числе их сложные химические соединения, включая органические), 3 - пыль (размеры пылинок 10-5 - 10-4 см), собранная вместе с газом в облака, 4 - потоки космических лучей, управляемые и удерживаемые магнитным полем Галактики и 5 - планеты с их спутниками, метеороиды и кометы (по крайней мере, всё это имеется в окрестности Солнца).

41

Млечный путь. Движение звезд в Галактике. Основные характеристики галактик. Виды галактик. Состав галактик. Звездные ассоциации. Работы академика В. А. Амбарцумяна. Красное смещение спектров и расширение метагалактики. Закон Хаббла. Теория Фридмана.

Мле́чный Путь (или Гала́ктика, с заглавной буквы) — галактика, в которой находятся Земля, Солнечная система и все звёзды, видимые невооружённым глазом. Относится к спиральным галактикам с перемычкой.

Во многих галактиках звёзды вращаются вокруг одной оси, образуя диск с шарообразным утолщением в центре, который часто называют - балдж (от английского bulde - выпуклость). В самом центре балджа находится ядро. Диск окружают звёзды, образуя сферическую подсистему, называемую гало (halo - сияние). Если бы такая вращающаяся галактическая система состояла из холодных, ничего не излучающих тел, то кинетическая энергия холодного тела каждой звезды равнялась бы его потенциальной энергии относительно центра масс галактики

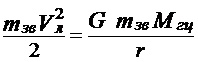 (1), где

mзв - масса звезды;

Mгц - масса галактического центра;

Vл - линейная скорость звезды;

G - гравитационная постоянная;

r- расстояние от галактического центра до звезды.

Виды галактик

S - Спиральная ( Spiral ) C - Компактная ( Compact ) E - Эллиптическая ( Ellipticals ) I - Неправильная ( Irregular ) D - Карликовая ( Dwarf ) L - Линзообразная ( S0 ) P - Специальная ( Peculiar ) B - С перемычкой ( Barred ) R - Кольцевая ( Ring )

В состав Галактики входят: 1 - звезды (одиночные, кратные, в шаровых и рассеянных скоплениях), 2 - межзвездный газ (атомарный, молекулярный водород, другие газы и в числе их сложные химические соединения, включая органические), 3 - пыль (размеры пылинок 10-5 - 10-4 см), собранная вместе с газом в облака, 4 - потоки космических лучей, управляемые и удерживаемые магнитным полем Галактики и 5 - планеты с их спутниками, метеороиды и кометы (по крайней мере, всё это имеется в окрестности Солнца).

Важнейшие интегральные характеристики галактик (экстремальные значения опущены):

Параметр	Основной метод измерения	Интервал значений	Примерное значение для нашей галактики
Диаметр D25	Фотометрия	5—50 кпк	30 кпк
Радиальная шкала диска R0	Фотометрия	1—7 кпк	3 кпк
Толщина звёздного диска	Фотометрия дисков, наблюдаемых «с ребра»	0,3—1 кпк	0,7 кпк
Светимость	Фотометрия	107—1011 Lʘ	5·1010 Lʘ
Масса М25 в пределах D25	Измерение скоростей газа и/или звёзд по эффекту Доплера	107—1012Mʘ	2·1011 Mʘ
Относительная масса газа Mgas/M25 в пределах D25	Измерение интенсивностей линий нейтрального и молекулярноговодорода	0,1—30 %	2%
Скорость вращения V внешних областей галактик	Измерение скоростей газа и/или звёзд по эффекту Доплера	50—300 км/с	220 км/с (для окрестности Солнца)
Период обращения внешних областей галактик	Измерение скоростей газа и/или звёзд по эффекту Доплера	108—109 лет	2·108 лет (для окрестности Солнца)
Масса центральной чёрной дыры	Измерение скоростей звёзд и газа вблизи ядра; эмпирическая зависимость от центральной дисперсии звёзд	3·105—3·109Mʘ	4·106 Mʘ

Звёздные ассоциации — группировки гравитационно несвязанных звёзд или слабосвязанных молодых (возраст до нескольких десятков миллионов лет) звёзд, объединённых общим происхождением.

В отличие от молодых рассеянных звёздных скоплений, звёздные ассоциации обладают бо́льшим размером (десятки парсек, у ядер рассеянных звёздных скоплений — единицы парсек) и меньшей плотностью: количество звёзд в ассоциации — от десятков до сотен (врассеянных звёздных скоплениях — от сотен до тысяч). Происхождением звёздные ассоциации обязаны областям звёздообразования комплексов молекулярных облаков.

Различают следующие типы звёздных ассоциаций:

OB-ассоциации, содержащие в основном массивные звёзды спектральных классов O и B

Т-ассоциации, содержащие в основном маломассивные переменные звёзды типа Т Тельца

R-ассоциации (от R — reflection), в которых звёзды спектральных классов O — A2 окружены отражательными газопылевыми туманностями.

Виктор Амазаспович Амбарцумян - выдающийся советский ученый, один из основателей теоретической астрофизики. Труды Амбарцумяна относятся к области физики звезд и туманностей, звездной астрономии, динамики звездных систем, космогонии звезд и галактик, математической физики. Амбарцумян является автором принципиально новой космогонической концепции. Амбарцумян - дважды лауреат Сталинской премии (1946,1950), дважды Герой Социалистического Труда (1968,1978) , лауреат Государственной премии Российской Федерации (1996), Национальный Герой Армении, обладатель многочисленных академических наград, основатель Бюраканской обсерватории.

Основные направления научной деятельности.

Физика оболочек звезд и газовых туманностей.

Динамика и статистическая механика звездных систем.

Природа межзвездной материи и теория флуктуаций.

Теория рассеяния света в мутной среде.

Звездные ассоциации и эволюция звезд.

Физика молодых звезд и источники звездной энергии.

Внегалактическая астрономия.

Красное смещение — наблюдаемое для всех далёких источников (галактики, квазары) понижение частот излучения, свидетельствующее о динамическом удалении этих источников друг от друга и, в частности, от нашей Галактики, т.е. о нестационарности (расширении) Метагалактики.

Красное смещение свидетельствует о расширении всей доступной наблюдениям части Вселенной; это явление обычно называется расширением (астрономической) Вселенной.

В теории относительности доплеровское красное смещение рассматривается как совместный результат движения источника относительно приёмника (обычный эффект Доплера) и замедления течения времени в движущейся системе отсчёта (поперечный эффект Доплера, эффект специальной теории относительности).

Зако́н Ха́ббла (закон всеобщего разбегания галактик) — эмпирический закон, связывающий красное смещение галактик и расстояние до них линейным образом.

Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности, первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.