17. Определение расстояний до тел солнечной системы по параллаксам светил. Радиолокационный метод.
Способы определения расстояний до тел Солнечной системы и их размеров. Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения. p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила. Радиолокационный метод. Он заключается в том, что на небесное тело посылают мощный кратковременный импульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние. Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.
Определение расстояний до тел Солнечной системы основано на измерении их горизонтальных параллаксов.
Зная горизонтальный экваториальный параллакс р0 светила, легко определить его расстояние от центра Земли (см. рис. 20). Действительно, если ТО = R0 есть экваториальный радиус Земли,ТМ = — расстояние от центра Земли до светила М, а угол р — горизонтальный экваториальный параллакс светила р0 , то из прямоугольного треугольника ТОМ имеем
|
(3.1) |
Для всех светил, кроме Луны, параллаксы очень малы. Поэтому формулу (3.1) можно написать иначе, положив
а именно,
|
(3.2) |
Расстояние получается в тех же единицах, в которых выражен радиус Земли R0. По формуле (3.2) определяются расстояния до тел Солнечной системы. Быстрое развитие радиотехники дало астрономам возможность определять расстояния до тел Солнечной системы радиолокационными методами. В 1946 г. была произведена радиолокация Луны, а в 1957-1963 гг.— радиолокация Солнца, Меркурия, Венеры, Марса и Юпитера. По скорости распространения радиоволн с = 3 105 км/сек и по промежутку времени t (сек) прохождения радиосигнала с Земли до небесного тела и обратно легко вычислить расстояние до небесного тела
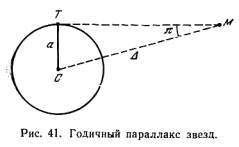
Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите (рис. 41).
Угол, под которым со звезды был бы виден средний радиус земной орбиты при условии, что направление на звезду перпендикулярно к радиусу, называется годичным параллаксом звезды .Если СТ = а есть средний радиус земной орбиты, МС = — расстояние звезды М от Солнца С, а угол — годичный параллакс звезды, то из прямоугольного треугольника СТМ имеем
|
(3.3) |
Годичные параллаксы звезд меньше 1", и поэтому
|
(3.4) |
Расстояние по этим формулам получается в тех же единицах, в которых выражено среднее расстояние а Земли от Солнца.